Leetcode 240. Search a 2D Matrix II

Write an efficient algorithm that searches for a value in an m x n matrix. This matrix has the following properties:

• Integers in each row are sorted in ascending from left to right.
• Integers in each column are sorted in ascending from top to bottom.

For example,

Consider the following matrix:

[
  [1,   4,  7, 11, 15],
  [2,   5,  8, 12, 19],
  [3,   6,  9, 16, 22],
  [10, 13, 14, 17, 24],
  [18, 21, 23, 26, 30]
]

Given target = 5, return true.

Given target = 20, return false.

---

解题思路：

从左下角往右上角找，若是小于target就往右找，若是大于target就往上找。时间复杂度O(m+n)  n 为行数，m为列数。

例如找136

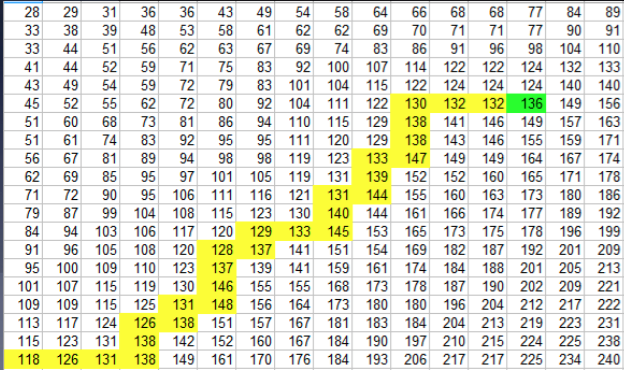
但Lintcode上类似题目问题变成找出多少个target，循环中稍微变化下，设置一个count, 就可以了。

---

Java code:

public class Solution {
    public boolean searchMatrix(int[][] matrix, int target) {
        //check corner case
        if(matrix == null || matrix.length == 0) {
            return false;
        }
        if(matrix[0] == null || matrix[0].length == 0) {
            return false;
        }
        //find from bottom left to top right
        int n = matrix.length; //row
        int m = matrix[0].length; //column
        int x = n-1;
        int y = 0;while ( x >= 0 && y < m) {
            if(matrix[x][y] < target) {
                y++;
            } else if (matrix[x][y] > target) {
                x--;
            } else {
                return true;
            }
        }
        return false;
    }
}

---

Reference:

1. http://www.jiuzhang.com/solutions/search-a-2d-matrix-ii/