Manacher 算法-----o(n)回文串算法

回文的含义是：正着看和倒着看相同，如abba和yyxyy

       Manacher算法基本要点：用一个非常巧妙的方式，将所有可能的奇数/偶数长度的回文子串都转换成了奇数长度：在每个字符的两边都插入一个特殊的符号。比如 abba 变成 #a#b#b#a#， aba变成 #a#b#a#。
为了进一步减少编码的复杂度，可以在字符串的开始加入另一个特殊字符，这样就不用特殊处理越界问题，比如$#a#b#a#。

P［id］：以字符str［id］为中心的最长回文串，当以str［id］为第一个字符时，这个最长回文串向右延伸了P［id］个字符。示例：

id： 0  1  2  3  4  5  6  7  8  9  10

str[id]： #  a  #  b  #  a  #  c  #  b   #

P[id]： 1  2  1  4  1  2  1  2  1  2  1

这里有一个很好的性质，P［id］-1就是该回文子串在原串中的长度。现在的关键问题就在于怎么在O（n）时间复杂度内求出P数组了。只要把这个P数组求出来，最长回文子串就可以直接扫一遍得出来了。

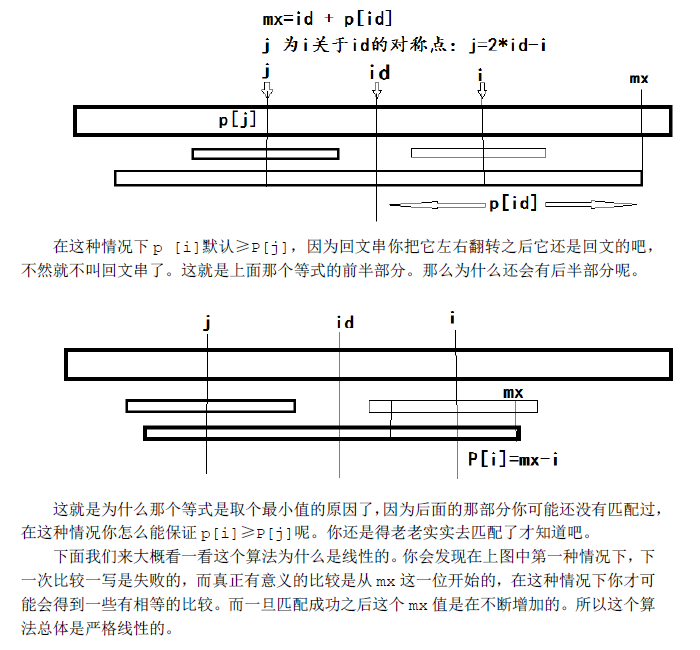
由于这个算法是线性从前往后扫的。那么当我们准备求P［i］的时候，i以前的P［j］我们是已经得到了的。我们用mx记在i之前的回文串中，延伸至最右端的位置。同时用id这个变量记下取得这个最优mx时的id值。（注：为了防止字符比较的时候越界，我在这个加了‘#’的字符串之前还加了另一个特殊字符‘$’，故我的新串下标是从1开始的）

好，到这里，我们可以先贴一份代码了。

	void getMaxPlalinStr(char[] s){
		int id = 0;  // 记录当前最大回文串的中心位置
		int max = 0; // 记录当前最大回文串的最右边界
		int len = s.length;
		int[] p = new int[len]; // 记录以每个字符为中心的回文串长度

		// 线性遍历，求解p[i]
		for(int i=0;i<len;i++){

			p[i] = max > i ? (p[2*id-i]<(max-i) ? p[2*id-i]:(max-i)) : 1;

			while(i-p[i]>=0 && i+p[i]<len && s[i+p[i]]==s[i-p[i]])
				p[i]++;
			if(p[i]+i > max){
				max = p[i]+i;
				id = i;
			}
		}
		max = 0;
		for(int i=0;i<len;i++){
			if(max < p[i]){
				max = p[i];
				id =i;
			}

		}
		System.out.println("id="+id+",max="+max);
	}

   代码是不是很短啊，而且相当好写。很方便吧，还记得我上面说的这个算法避免了很多不必要的重复匹配吧。这是什么意思呢，其实这就是一句代码。

p[i] = max > i ? (p[2*id-i]<(max-i) ? p[2*id-i]:(max-i)) : 1;

就是当前面比较的最远长度mx>i的时候，P［i］有一个最小值。这个算法的核心思想就在这里，为什么P数组满足这样一个性质呢?

   （下面的部分为图片形式）

参考：http://blog.csdn.net/ggggiqnypgjg/article/details/6645824