algorithm@ KMP

一. KMP算法

KMP算法是一种改进的字符串匹配算法，由D.E.Knuth与V.R.Pratt和J.H.Morris同时发现，简称KMP算法。KMP算法的关键是利用匹配失败后的信息，尽量减少模式串与主串的匹配次数以达到快速匹配的目的。具体实现就是实现一个next()函数，函数本身包含了模式串的局部匹配信息。

二. KMP算法的意义

先举一个简单模式匹配的例子，给定字符串T=“abababca”，S=“bacbababaabcbab”，判断T是否是S的子串，如果用暴力扫描的话，就是拿着T字符串从S的头扫到尾。这样的时间复杂度最坏情况下是O（n*m），其中n和m分别是主串和模式串的长度。而KMP算法的时间消耗是O（n+m）的，至于为什么这样，下面再说。

三. KMP算法的核心

KMP的核心就是一张表，我们称之为部分匹配表，起初我看这张表的时候也是云山雾绕，不知所云，部分匹配表是为模式串T专门设计的，T中每个字符对应着一个整数值，（这个地方也是困扰了我很久），现在我尽可能说得明白一些。首先下面附上一张T为“abababca”的部分匹配图，让大家“先睹为快”，看看部分匹配表是个什么东东。

好了，现在我们有了一个含有8个字符的模式串T，那么最后一行的value值是怎么得来的呢？别急，我先介绍相关概念：前缀和后缀，就拿字符串”abca“来说，”abca“的前缀有{a，ab，abc}，”abca”的后缀有“bca，ca，a”，怎么样，很好理解对吧？一个字符串的前缀就是除了该字符串的最后一个字符以外的从首字符开始的连续字符串（自己胡乱下的定义，可能不准确，不过没关系，理解意思就行），后缀定义也类似。那么像字符串”a“就既没有前缀也没有后缀。

有了上面这两个概念，我们就可以得出value是怎么来的了。value值就是"前缀"和"后缀"的最长的共有元素的长度，这里就直接讲解例子帮助消化理解。首先我们把目光聚焦到index=0位的字符‘a’上来，字符串”a“没有前缀，没有后缀，共有元素为0，所以value[0]=0。然后index=1，字符串”ab“，前缀集合为{a}，后缀集合为{b}，没有共有元素，value[1]=0。index=2,字符串“aba”，前缀集合为{a，ab}，后缀集合为{ba，a}，共有元素为{a}，取长度最长的，所以value[2]=1. index=3，字符串“abab”，前缀集合为{a，ab，aba}，后缀集合为{bab，ab，b}，共有元素为{ab}，value[3]=2. index=4，字符串“ababa”，前缀集合为{a，ab，aba，abab}，后缀集合为{baba，aba，ba，a}，共有元素为{aba}，所以value[4]=3. index=5，字符串“ababab”，前缀集合为{a，ab，aba，abab，ababa}，后缀集合为{babab，abab，bab，ab，b}，共有元素是{abab，ab}，value[5]=4. index=6，字符串“abababc”，前缀集合是{a，ab，aba，abab，ababa，ababab}，后缀集合是{bababc，ababc，babc，abc，bc，c}，没有共有元素，所以value[6]=0. index=7，字符串“abababca”，前缀集合是{a，ab，aba，abab，ababa，ababab，abababc}，后缀集合是{bababca，ababca，babca，abca，bca，ca，a}，共有元素是{a}，value[7]=1.这下算出value来应该是驾轻就熟了吧。

四. KMP算法运行

部分匹配表我们已经可以算出来了，现在就是要用这张表来运行KMP算法。这里以T=“abcdabd”，S=“abcdab abcdabcdabde”为例说明,这里首先给出T的部分匹配表：

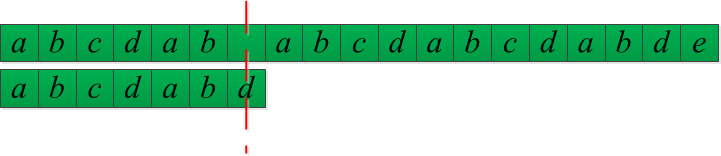
初始状态，‘d’和‘ ’不匹配，但是‘d’前面的部分“abcdab”匹配，所以我们查询部分匹配表，得到value[5]=2，所以我们把T向右移动（6-2）个单位，6是部分匹配的长度，2是部分匹配字符串的value值。

如红线标注，’c‘和’ ‘不匹配，但是’c‘前面部分“ab”部分匹配，所以我们查表，得到value[1]=0，所以我们吧T向右移动（2-0）个单位。2是部分匹配的长度，0表示value值。

如红线标注，’a‘和’ ‘不匹配，而且’a‘前面什么也没有，就也没有部分匹配，那部分匹配表中查不到怎么办呢？对于这种情况，我们默认是T向右移动一个单位。

如红线所示，’c‘与’d‘不匹配，但是T中’d'以前的部分”abcdab“匹配了，所以我们查询部分匹配表，value[5]=2，所以模式串T向右移动（6-2）个单位。

“SUCCESS！”，我们找到了S的子串与T相等。如果你只想找到S中的一处与T相等，那么你就可以终止算法了，如果你还想找到S中第二个出现“ancdabd”的位置，那么你就向右移动（7-0）位，后面的过程和上面一样的，这里就不再赘述。

五. 总结

可能大家会发现部分匹配表与我们在书本上或者一些博客上看到的不一样，书本上用的是next数组，next[x]中的x表示的是匹配失败处字符的下标，假设我们在匹配的过程中发现T[x]!=S[i] (1<=i<=s.len)，那么我们就查看T[1],T[2],...T[x-1]的部分匹配值，对！，就是上面讲的部分匹配表！回顾上面的例子我们可以发现，当T[x]处匹配失败时，我们查看的value[x-1]处的值，换言之，next[x]=value[x-1]!!。所以我们会看到next[0]=-1，因为没有value[-1]这种东西嘛~~。

六. next数组的源代码

 void getNext(char *T){
     int j=,k=-;
     next[]=-;
     while(j<strlen(T)-1){
         if(k==-||T[j]==T[k]){
             j++; k++;
             next[j]=k;
         }
         else k=next[k];    
       }
 }