数据结构（KD树）：HDU 4347 The Closest M Points

The Closest M Points

Time Limit: 16000/8000 MS (Java/Others)    Memory Limit: 98304/98304 K (Java/Others)
Total Submission(s): 3285    Accepted Submission(s): 1201

Problem Description

The
course of Software Design and Development Practice is objectionable.
ZLC is facing a serious problem .There are many points in K-dimensional
space .Given a point. ZLC need to find out the closest m points.
Euclidean distance is used as the distance metric between two points.
The Euclidean distance between points p and q is the length of the line
segment connecting them.In Cartesian coordinates, if p = (p₁, p₂,..., p_n) and q = (q₁, q₂,..., q_n) are two points in Euclidean n-space, then the distance from p to q, or from q to p is given by:

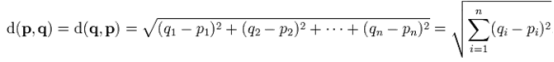
Can you help him solve this problem?

 

Input

In
the first line of the text file .there are two non-negative integers n
and K. They denote respectively: the number of points, 1 <= n <=
50000, and the number of Dimensions,1 <= K <= 5. In each of the
following n lines there is written k integers, representing the
coordinates of a point. This followed by a line with one positive
integer t, representing the number of queries,1 <= t <=10000.each
query contains two lines. The k integers in the first line represent the
given point. In the second line, there is one integer m, the number of
closest points you should find,1 <= m <=10. The absolute value of
all the coordinates will not be more than 10000.
There are multiple test cases. Process to end of file.

 

Output

For each query, output m+1 lines:
The first line saying :”the closest m points are:” where m is the number of the points.
The following m lines representing m points ,in accordance with the order from near to far
It
is guaranteed that the answer can only be formed in one ways. The
distances from the given point to all the nearest m+1 points are
different. That means input like this:
2 2
1 1
3 3
1
2 2
1
will not exist.

 

Sample Input

3 2
1 1
1 3
3 4
2
2 3
2
2 3
1

 

Sample Output

the closest 2 points are:
1 3
3 4
the closest 1 points are:
1 3

　　

　　绳命中第一道KD树，模板题，照着打的。

　　难道————KD树==剪枝？嗯，我再想想~~

 #include <algorithm>
 #include <iostream>
 #include <cstring>
 #include <cstdio>
 #include <queue>
 using namespace std;
 const int maxn=;
 int cmpNo,K;
 struct Node{
     int x[],l,r,id;
     bool operator <(const Node &b)const{
         return x[cmpNo]<b.x[cmpNo];
     }
 };
 
 long long Dis(const Node &a,const Node &b){
     long long ret=;
     for(int i=;i<K;i++)
         ret+=(a.x[i]-b.x[i])*(a.x[i]-b.x[i]);
     return ret;
 }
 
 Node p[maxn];
 
 int Build(int l,int r,int d){
     if(l>r)return ;
     cmpNo=d;
     int mid=l+r>>;
     nth_element(p+l,p+mid,p+r+);
     p[mid].l=Build(l,mid-,(d+)%K);
     p[mid].r=Build(mid+,r,(d+)%K);
     return mid;
 }
 
 priority_queue<pair<long long,int> >q;
 void Kth(int l,int r,Node tar,int k,int d){
     if(l>r)return;
     int mid=l+r>>;
     pair<long long,int>v=make_pair(Dis(p[mid],tar),p[mid].id);
     if(q.size()==k&&v<q.top())q.pop();
     if(q.size()<k)q.push(v);
     long long t=tar.x[d]-p[mid].x[d];
     if(t<=){
         Kth(l,mid-,tar,k,(d+)%K);
         if(q.top().first>t*t)
             Kth(mid+,r,tar,k,(d+)%K);
     }
     else{
         Kth(mid+,r,tar,k,(d+)%K);
         if(q.top().first>t*t)
             Kth(l,mid-,tar,k,(d+)%K);
     }
 }
 int k,ans[];
 Node a[maxn];
 int main(){
     int n;
     while(scanf("%d%d",&n,&K)!=EOF){
         for(int id=;id<=n;id++){
             for(int i=;i<K;i++)
                 scanf("%d",&p[id].x[i]);
             p[id].id=id;
             a[id]=p[id];
         }
         Build(,n,);
         int Q,tot;
         scanf("%d",&Q);
         Node tar;
         while(Q--){
             for(int i=;i<K;i++)
                 scanf("%d",&tar.x[i]);
             scanf("%d",&k);
             printf("the closest %d points are:\n",k);
             for(int i=;i<=k;i++)q.push(make_pair(1e18,-));
             Kth(,n,tar,k,);tot=;
             while(!q.empty()){
                 int id=(q.top()).second;q.pop();
                 ans[tot++]=id;
             }
             for(int i=tot-;i>=;i--)
                 for(int j=;j<K;j++)
                     printf("%d%c",a[ans[i]].x[j],j==K-?'\n':' ');
         }
     }
     return ;
 }