Mark Compact GC (Part one: Lisp2)

目录

• 什么是GC 标记-压缩算法
  • Lisp2 算法的对象
  • 概要
• 步骤
  • 步骤一：设定forwarding指针
  • 步骤二：更新指针
  • 步骤三：移动对象
• 优缺点

什么是GC 标记-压缩算法

需要对标记清除和GC复制算法有一定了解

GC标记-压缩算法是由标记阶段和压缩阶段构成。

标记阶段和标记清除的标记阶段完全一样。之后我们要通过搜索数次堆来进行压缩。

Lisp2 算法的对象

Donald E.Knuth

对象结构如图示：

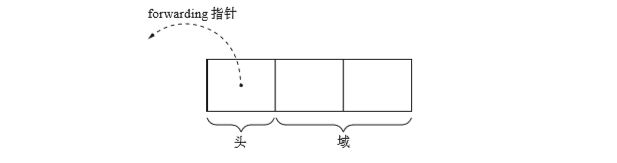
Lisp2 算法在对象头中为forwarding指针留出空间，forwarding指针表示对象的目标地点。（设定forwarding时，还不存在移动完毕的对象）

概要

假设我们在下图所示的状态下执行GC

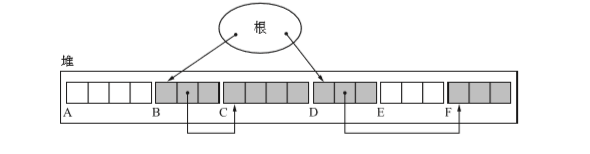
标记完后状态如下（过程与标记清除算法相同）

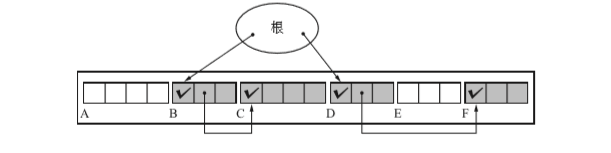
压缩完后的状态如下（可以看到，他们现在的位置是挨着的。）

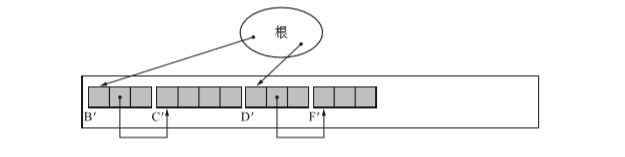
这种算法并不会对对象的顺序产生影响，知识缩小了他们之间的空隙，让他们聚集在堆的一端。

步骤

压缩阶段代码

compaction_phase(){
    set_forwarding_ptr() // 设置forwarding指针
    adjust_ptr() // 更新指针
    move_obj() // 移动对象
}

步骤一：设定forwarding指针

首先程序会搜索整个堆，给活动的对象设定forwarding指针。初始状态下forwarding是NULL。

set_fowarding_ptr(){
    scan = new_address = $heap_start
    while(scan < $heap_end)
        if(scan.mark = TRUE)
            scan.forwarding = new_address
            new_address += scan.size
        scan += scan.size
}

• scan 用来搜索堆中的指针，new_address指向目标地点的指针。
• 一旦scan找到活动对象，forwarding指针就要被更新。按着new_address对象的长度移动。
• 如下图示：

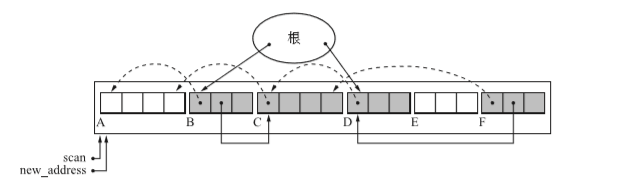
步骤二：更新指针

adjust_ptr(){
    for(r :$roots)  // 更新根对象的指针
        *r = (*r).forwarding
    scan = $heap_start
    while(scan < $heap_end)
        if(scan.mark == TRUE)
            for(child :children(scan)) // 通过scan 更新其他对象指针
                *child = (*child).forwarding
        scan += scan.size
}

• 首先更新根的指针
• 然后重写所有活动对象的指针（对堆进行第二次的搜索）
  
  

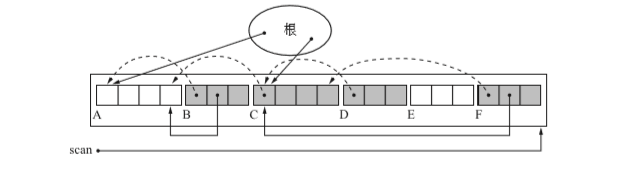
步骤三：移动对象

搜索整个堆（第三次搜索），再将对象移动到forwarding指针的引用处。

move_obj(){
   scan = $free = $heap_start
   while(scan < $heap_end)
    if(scan.mark == TRUE) // 判断是否是活动对象
        new_address = scan.forwarding  // 获取对象要移动的地点
        copy_data(new_address, scan, scan.size) // 复制对象（移动对象）
        new_address.forwarding = NULL // 将forwarding改为NULL
        new_address.mark = FALSE // mark改为FALSE
        $free += new_address.size // 指针后移
        scan += scan.size // 指针后移
}

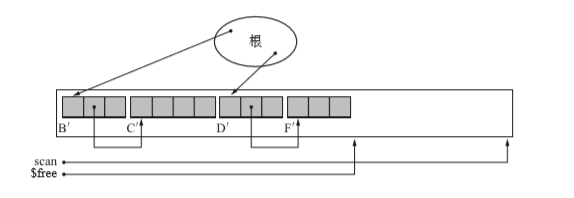
• 算法不会对对象本身的顺序进行改变，只会把对象集中在堆的一端。
• 算法没有去删除对象，知识吧对象的mark设置为FALSE
• 之后把forwarding改为NULL，标志位改为FALSE，将$free移动obj.size个长度。

优缺点

优点：可有效利用堆

使用整个堆在进行垃圾回收，没啥说的。任何的算法都是有得有失，用时间换空间。或者用空间换时间。重要的是它在这里

适不适用。

缺点：压缩花费计算成本

Lisp2 算法中，对堆进行了3次搜索。在搜索时间与堆大小成正相关的状态下，三次搜索花费的时间是很恐怖。也就是说，它的吞吐量要低于其他算法。时间成本至少是标记清除的三倍（当然不包含mutator）