iOS 使用贝塞尔曲线绘制路径

使用贝塞尔曲线绘制路径

大多数时候，我们在开发中使用的控件的边框是矩形，或者做一点圆角，是使得矩形的角看起来更加的圆滑。 但是如果我们想要一个不规则的图形怎么办？有人说，叫UI妹子做，不仅省事，还可以趁机接近她们（_:D）。这又时候确实可以。但是如果是一个时刻变动的不规则图形，这样如果做成动图或者剪出很多张图，再叫UI妹子做的话，似乎也能解决， 但是实际效果吧，呵呵。好吧，iOS中我们其实不需要担心这个问题。使用UIBezierPath可以很容易的会址出一些复杂的图形。

UIBezierPath 属于UIkit，可以用于绘制路径。 说到绘制，大家很快想到了大名鼎鼎的Core Graphics，同学们直接使用 Core Graphics绘制图形也完全没有问题，Core Graphics具有更多的绘制途径，它是一套强大的API，但是其函数之多异常绝对会让不熟悉的你头晕脑胀，iOS 很人性化的对 Core Graphics进行封装。也即是UIBezierPath。这篇文章主要讲解下如何使用UIBezierPath结合CAShapeLayer在一个UIView上绘制简单的路径。

对于路径的绘制两种方式，一种是填充（fill ），一种是描绘（stroke）。直接上代码吧，毕竟也不是什么高深的知识。

import UIKit

class ViewController: UIViewController {

    override func viewDidLoad() {
        super.viewDidLoad()
        self.userBezier()
    }

    override func didReceiveMemoryWarning() {
        super.didReceiveMemoryWarning()
    }

    func userBezier(){
        // 绘制一段圆弧   如果是合起来的就是圆了
        let criclePath: UIBezierPath = UIBezierPath.init(arcCenter: CGPoint.init(x: , y: ), radius: , startAngle: , endAngle: 5.12, clockwise: true)
        criclePath.stroke()

        // 绘制一个矩形
        let rectPath: UIBezierPath = UIBezierPath.init(rect: CGRect.init(x: , y: , width: , height: ))
        criclePath.append(rectPath)

        // 绘制一个椭圆  原理是内接矩形，如果矩形的长宽相等那么绘制的就是圆
        let ovalPath:UIBezierPath = UIBezierPath.init(ovalIn: CGRect.init(x: , y: , width: , height: ))
        criclePath.append(ovalPath)

        //绘制直线多边形  可以让多条直线拼接 组合成复杂的形状  比如绘制一个三角形
        let trianglePath :UIBezierPath = UIBezierPath.init()
        trianglePath.move(to: CGPoint.init(x: , y: ))  //绘制起始点
        trianglePath.addLine(to: CGPoint.init(x: , y: ))  //从起点绘制一条直线到指定点
        trianglePath.addLine(to: CGPoint.init(x: , y: ))  //
        trianglePath.close()   //闭合路径
        trianglePath.lineWidth = 3.0
        criclePath.append(trianglePath)

        //添加一个二阶的曲线  二阶曲线一共是三个点， 起点／终点／折点（控制点）
        let cruvePath :UIBezierPath = UIBezierPath.init()

        cruvePath.move(to: CGPoint.init(x: , y: ))
        cruvePath.addQuadCurve(to: CGPoint.init(x: , y: ), controlPoint: CGPoint.init(x: , y: ))
        criclePath.append(cruvePath)

        //添加一个三阶的曲线  起点 终点  两个控制点 后面可以无限添加 二阶曲线  形成一个很长的三阶曲线
        let path :UIBezierPath = UIBezierPath.init()
        path.move(to: CGPoint.init(x: , y: ))
        path.addCurve(to: CGPoint.init(x: , y: ), controlPoint1: CGPoint.init(x: , y: ), controlPoint2: CGPoint.init(x: , y: ))
        path.addQuadCurve(to: CGPoint.init(x: , y: ), controlPoint: CGPoint.init(x: , y: ))
        criclePath.append(path)

        //创建一个CAShapelayer  用于显示这些路径
        let shPl: CAShapeLayer = CAShapeLayer.init()
        shPl.path = criclePath.cgPath
        shPl.lineWidth = 3.0
        shPl.fillColor = UIColor.clear.cgColor  //填充路径

        shPl.strokeColor = UIColor.red.cgColor   //描绘路径 根据线宽来描绘

        self.view.layer.addSublayer(shPl)
        self.view.layer.backgroundColor = UIColor.white.cgColor

    }

}

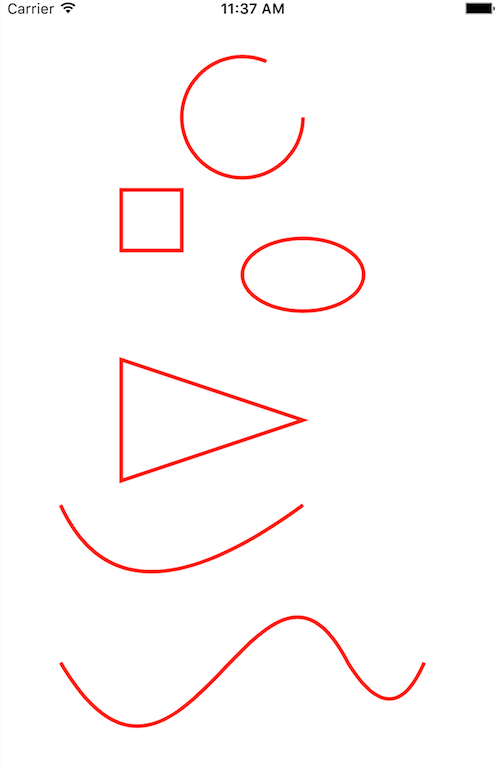
根据绘制的方式不同，运行下面两张图片：