[ACM] POJ 1942 Paths on a Grid (组合）

Paths on a Grid

Time Limit: 1000MS		Memory Limit: 30000K
Total Submissions: 21297		Accepted: 5212

Description

Imagine you are attending your math lesson at school. Once again, you are bored because your teacher tells things that you already mastered years ago (this time he's explaining that (a+b)²=a²+2ab+b²). So you decide to waste
your time with drawing modern art instead. 



Fortunately you have a piece of squared paper and you choose a rectangle of size n*m on the paper. Let's call this rectangle together with the lines it contains a grid. Starting at the lower left corner of the grid, you move your pencil to the upper right corner,
taking care that it stays on the lines and moves only to the right or up. The result is shown on the left: 




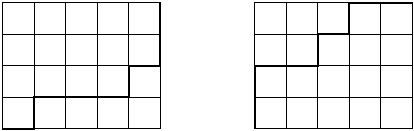
Really a masterpiece, isn't it? Repeating the procedure one more time, you arrive with the picture shown on the right. Now you wonder: how many different works of art can you produce?

Input

The input contains several testcases. Each is specified by two unsigned 32-bit integers n and m, denoting the size of the rectangle. As you can observe, the number of lines of the corresponding grid is one more in each dimension. Input is terminated by n=m=0.

Output

For each test case output on a line the number of different art works that can be generated using the procedure described above. That is, how many paths are there on a grid where each step of the path consists of moving one unit to the right or one unit up?
You may safely assume that this number fits into a 32-bit unsigned integer.

Sample Input

5 4
1 1
0 0

Sample Output

126
2

Source

Ulm Local 2002

简单题，求解 C(n+m, m） .

代码：

#include <iostream>
#include <algorithm>
using namespace std;

long long c(long long n,long long m)
{
    long long ans=1;
    for(int i=1;i<=m;i++)
        ans=ans*(n--)/i;
    return ans;
}

int main()
{
    long long n,m;
    while(cin>>n>>m&&(n||m))
    {
        if(n<m)
            swap(n,m);
        cout<<c(n+m,m)<<endl;
    }
    return 0;
}

http://blog.csdn.net/lyy289065406/article/details/6648516在里面学到了两种新的求解组合数的方法。

处理阶乘有三种办法：

（1）       传统意义上的直接递归。n的规模最多到20+，太小了，在本题不适用，并且很慢

（2）       稍快一点的算法，就是利用log()化乘为加。n的规模尽管扩展到1000+，可是因为要用三重循环，一旦n规模变得更大。耗时就会很之严重,时间复杂度达到O(n*m*(n-m))，本题规定了n，m用unsigned int32类型，就是说n,m的规模达到了21E以上。铁定TLE的。

并且就算抛开时间不算，还存在一个致命的问题，就是精度损失随着n的添加会变得很严重。

由于n有多大。就要进行n次对数运算。n规模一旦过大，就会丢失得很严重了。所以这样的方法是绝对不可取的，由于中途的精度丢失不是简单的四舍五入能够挽回的。

（3）       拆分阶乘。逐项相除，再乘曾经面全部项之积。

这样的方法用一个循环就OK了。时间复杂度仅仅有O(n-m)，很可观。

 

 以下我依据程序具体说说算法（3）：

       double cnm=1.0;

       while(b>0)

              cnm*=(double)(a- -)/(double)(b- -);

 

这是我写的函数原型。计算的是 aCb

这样的算法巧妙地利用了分子分母的关系，而不是把公示中的3个阶乘单独处理。

比如当 a=5,b=2时

因为用了 double去计算组合数。那么最后要转化为 无符号整型 时就要处理精度问题，有两种方法：四舍五入+强制类型转换  或者 用 setprecision()函数

1. unsigned comp(unsigned n,unsigned m)
2. {
3. unsigned a=m+n;
4. unsigned b=(m<n?m:n);
5. double cnm=1.0;
6. while(b>0)
7. cnm*=(double)(a--)/(double)(b--);
8. cnm+=0.5;      //double转unsigned会强制截断小数。必须先四舍五入
9. return (unsigned)cnm;
10. }

1. double comp(unsigned n,unsigned m)
2. {
3. unsigned a=m+n;
4. unsigned b=(m<n?m:n);
5. double cnm=1.0;
6. while(b>0)
7. cnm*=(double)(a--)/(double)(b--);
8. return cnm;
9. }

1. cout<<fixed<<setprecision(0)<<comp(n,m)<<endl;
2. //fixed是为了固定小数位数
3. //setprecision()函数是会自己主动四舍五入的，所以不用像强制类型转换那样预先+0.5