P3376 【模板】网络最大流(luogu)

P3376 【模板】网络最大流(luogu)

最大流的dinic算法模板(采取了多种优化)

优化	时间
inline+当前弧+炸点+多路增广	174ms
no 当前弧	175ms
no 炸点	249

自己对最大流算法的理解:

通过bfs对剩余图进行分层，剩余图中有流量的边(cap>0)才能bfs,然后dfs找增广路(满足dis[v]==dis[u]+1&&cap(u,v)>0)

各种优化(基本是在dfs(s,flow)上做的)的实现思路:

• 多路增广
  
  通过记录从s流出的各个边增广的和，而不是找到目标t就返回(可以比较一下两段代码

//当前弧优化效果不明显可不加
struct Edge{
    int v,nxt,cap;
}es[maxm];
void add(int u,int v,int cap){
    //printf("db add %d->%d %d\n",u,v,cap);
    es[cnt].v=v,es[cnt].cap=cap,es[cnt].nxt=head[u];
    head[u]=cnt,cnt++;
}
int bfs(int s,int des){
    CL(dep,-1);
    queue<int> q;q.push(s);
    dep[s]=1;
    while(!q.empty()){
        int tmp=q.front();q.pop();
        for(int t=head[tmp];t!=-1;t=es[t].nxt){
            int v=es[t].v,cap=es[t].cap;
            if(cap>0&&dep[v]==-1){//dep[v]==-1代表未访问过
                dep[v]=dep[tmp]+1;q.push(v);
                if(v==des) return 1;
            }
        }
    }
    return dep[des]>-1?1:0;//是否能到达目的节点
}
int dfs(int s,int fl,int des){//fl流入s的流量,向s的出边增光
    if(s==des||fl<=0) return fl;
    int res=0; //多路增光
    for(int t=head[s];fl&&t!=-1;t=es[t].nxt){
        int v=es[t].v,cap=es[t].cap;
        if(dep[v]==dep[s]+1){
            int f=dfs(v,min(fl,cap),des);
            es[t].cap-=f,es[t^1].cap+=f,res+=f;
            fl-=f;
        }
    }
    if(res==0) dep[s]=-2;//炸点优化
    return res;
}

所以朴素的方式往往需要一次bfs,多次dfs;而经过多路扩展则是一次bfs，一次dfs(因为一次dfs就找全了所有增广路)

• 当前弧优化
  
  思想是记录节点s应该流向的边,假设有这样s->1,s->2,s->3假设s->2时流量flow已经耗尽,那么下一次从3流出的应该从s->2开始(注意流向s可能有多条路径,flow只是流向s的某一条路径的流量)

for(int x=cur[s];x!=-1;x=e[x].next){
        cur[s]=x;//当前弧优化
        if(d[e[x].v]==d[s]+1&&e[x].cap>0){
            //....
            if(!flow) break;//当前已经没有流量
        }
    }

• 炸点优化
  
  一个非目的点，流不出任何流量，那么以后都不用向该点流，所以d[s]=-2(以后dfs都不会流向它)

代码

//dinic 算法处理最大流问题
#include<bits/stdc++.h>
using namespace std;
#define inf 0x3f3f3f3f
const int  maxn=1e4+10;
const int maxm=1e5+10;
int s,t,n,m;
struct Edge{
    int v,next,cap;
}e[maxm<<1];// begin from 0
int head[maxn];//-1 init
int cnt=-1;
int d[maxn];//init inf
int que[maxn<<2];
int cur[maxn];//for 当前弧优化

inline void add(int u,int v,int cap){//边从0开始
    //e[cnt]=(Edge){v,head[u],cap};
    cnt++;
    e[cnt].v=v,e[cnt].next=head[u],e[cnt].cap=cap;
    head[u]=cnt;
}
inline bool bfs(int ss,int tt){
    memset(d,inf,sizeof(d));
    memcpy(cur,head,sizeof(head));
    int h=0,t=1;
    que[0]=ss,d[ss]=1;
    while(t>h){
        int u=que[h];
        h++;
        for(int x=head[u];x!=-1;x=e[x].next){
            int v=e[x].v;
            if(d[v]>=inf&&e[x].cap>0){
                d[v]=d[u]+1;//d[]用作vis[]
                que[t++]=v;
            }
        }
    }
    //printf("db %d\n",d[tt]);
    return d[tt]<inf;
}
inline int dfs(int s,int flow){
    if(s==t||flow<=0) return flow;
    int res=0;
    for(int x=cur[s];x!=-1;x=e[x].next){
        cur[s]=x;//当前弧优化
        if(d[e[x].v]==d[s]+1&&e[x].cap>0){
        int f=dfs(e[x].v,min(flow,e[x].cap));
        e[x].cap-=f;
        e[x^1].cap+=f;
        res+=f;//通过res记录多路扩展
        flow-=f;
        if(!flow) break;//当前已经没有流量
        }
    }
    if(!res) d[s]=-2;//炸点优化,s没能流出任何流量，那么本次bfs下的dfs无需再向s流
    return res;
}
inline void dbgraph(){
    for(int i=1;i<=n;i++){
        printf("%d:",i);
        for(int x=head[i];x!=-1;x=e[x].next){
            if(e[x].cap>0) printf("%d\t",e[x].v);
        }
        printf("\n");
    }
}
int main(){
    //freopen("in.txt","r",stdin);
    scanf("%d %d %d %d",&n,&m,&s,&t);
    memset(head,-1,sizeof(head));
    for(int i=1;i<=m;i++){
        int u,v,cap;
        scanf("%d %d %d",&u,&v,&cap);
        add(u,v,cap);
        add(v,u,0);
    }
    //dbgraph();
    int  ans=0;
    while(bfs(s,t)){
            //printf("in bfs\n");
        ans+=dfs(s,inf);
    }
    printf("%d\n",ans);
    //fclose(stdin);
    return 0;

}

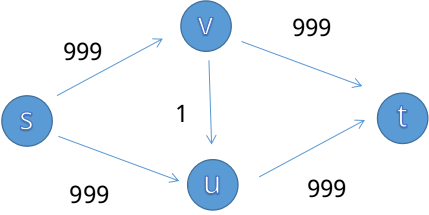
补充一点

从EK算法到Dinic算法有很重要的原因在于下面一张图