51nod1103 N的倍数

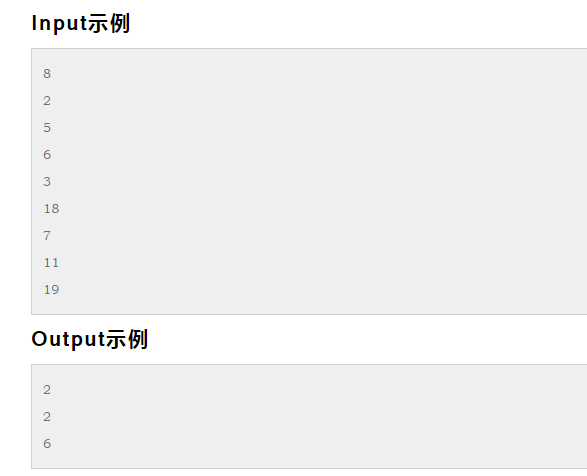
【题解】

先预处理出模N意义下的前缀和sum[i]。

1.如果sum[i]=0，那么1~i的数之和就是N的倍数

2.sum[i]%N总共有0~N-1这N种情况；根据1，如果sum[i]为0则必定有解；如果不存在sum[i]=0，那么根据抽屉原理，有N个前缀和，N-1种情况，那么一定存在sum[i]=sum[j]，那么i+1~j的数之和就是N的倍数

由上可知，一定存在一种方案满足取出连续的一些数使得这些数的和是N的倍数

 #include<cstdio>
 #include<algorithm>
 using namespace std;
 const int maxn=;
 int n,a[maxn],sum[maxn],last[maxn];
 void read(int &k){
     k=; int f=; char c=getchar();
     while (c<''||c>'')c=='-'&&(f=-),c=getchar();
     while (''<=c&&c<='')k=k*+c-'',c=getchar();
     k*=f;
 }
 int main(){
     read(n);
     for (int i=;i<=n;i++) read(a[i]),sum[i]=(sum[i-]+a[i])%n;
     for (int i=;i<=n;i++){
         if (sum[i]==){
             printf("%d\n",i);
             for (int j=;j<=i;j++) printf("%d\n",a[j]);
             return ;
         }
         else if (last[sum[i]]){
             printf("%d\n",i-last[sum[i]]);
             for (int j=last[sum[i]]+;j<=i;j++) printf("%d\n",a[j]);
             return ;
         }
         last[sum[i]]=i;
     }
 }