codeforces 446C DZY Loves Fibonacci Numbers 数论+线段树成段更新

DZY Loves Fibonacci Numbers

Time Limit:4000MS     Memory Limit:262144KB     64bit IO Format:%I64d & %I64u

Submit Status

Appoint description: 
System Crawler  (2014-07-14)

Description

In mathematical terms, the sequence F_n of Fibonacci numbers is defined by the recurrence relation

F₁ = 1; F₂ = 1; F_n = F_n - 1 + F_n - 2 (n > 2).

DZY loves Fibonacci numbers very much. Today DZY gives you an array consisting of n integers: a₁, a₂, ..., a_n. Moreover, there arem queries, each query has one of the two types:

1. Format of the query "1 lr". In reply to the query, you need to add F_{i - l + 1} to each element a_i, where l ≤ i ≤ r.
2. Format of the query "2 lr". In reply to the query you should output the value of 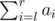 modulo 1000000009 (10⁹ + 9).

Help DZY reply to all the queries.

Input

The first line of the input contains two integers n and m (1 ≤ n, m ≤ 300000). The second line contains n integers a₁, a₂, ..., a_n (1 ≤ a_i ≤ 10⁹) — initial array a.

Then, m lines follow. A single line describes a single query in the format given in the statement. It is guaranteed that for each query inequality 1 ≤ l ≤ r ≤ n holds.

Output

For each query of the second type, print the value of the sum on a single line.

Sample Input

Input

4 4
1 2 3 4
1 1 4
2 1 4
1 2 4
2 1 3

Output

17
12

Hint

After the first query, a = [2, 3, 5, 7].

For the second query, sum = 2 + 3 + 5 + 7 = 17.

After the third query, a = [2, 4, 6, 9].

For the fourth query, sum = 2 + 4 + 6 = 12.

解题思路：根据斐波那契数列的两个定义(任意区间适应，a为该区间的第一项，b为该区间的第二项)：

(1)F(n)=b*fib[n-1]+a*fib[n-2] ;

(2)F[1]+F[2]+...+F[n]=F[n+2]-b;

 #include <iostream>
 #include <cstdio>
 #include <cstring>
 using namespace std;

 #define lson i<<1
 #define rson i<<1|1
 #define mid ((l+r)>>1)
 typedef __int64 LL;
 const int maxn=;
 const int mod=1e9+;
 int a[maxn],fib[maxn];

 struct Node
 {
     int f1,f2;//区间第一项和第二项的值
     int sum;
 }segtree[maxn<<];

 void init()//斐波那契数列预处理
 {
     fib[]=;fib[]=;
     for(int i=;i<maxn;i++)
         if((fib[i]=fib[i-]+fib[i-])>=mod)
             fib[i]-=mod;
 }

 int get_fib(int a,int b,int n)
 {
     if(n==) return a;
     if(n==) return b;
     return ((LL)b*fib[n-]+(LL)a*fib[n-])%mod;
 }

 int get_sum(int a,int b,int n)
 {
     int sum=get_fib(a,b,n+)-b;
     return (sum+mod)%mod;
 }
 void add_fib(int i,int l,int r,int a,int b)
 {
     segtree[i].f1=(segtree[i].f1+a)%mod;
     segtree[i].f2=(segtree[i].f2+b)%mod;
     segtree[i].sum=(segtree[i].sum+get_sum(a,b,r-l+))%mod;
 }

 void pushdown(int i,int l,int r)
 {
     add_fib(lson,l,mid,segtree[i].f1,segtree[i].f2);
     add_fib(rson,mid+,r,get_fib(segtree[i].f1,segtree[i].f2,mid+-l+)
         ,get_fib(segtree[i].f1,segtree[i].f2,mid-l+));
     segtree[i].f1=segtree[i].f2=;
 }

 void pushup(int i)
 {
     segtree[i].sum=(segtree[lson].sum+segtree[rson].sum)%mod;
 }

 void build(int i,int l,int r)
 {
     if(l==r)
     {
         segtree[i].sum=a[l];
         segtree[i].f1=segtree[i].f2=;
         return ;
     }
     build(lson,l,mid);
     build(rson,mid+,r);
     pushup(i);
 }

 void update(int i,int l,int r,int a,int b)
 {
     if(a<=l && r<=b)
     {
         add_fib(i,l,r,fib[l-a+],fib[l-a+]);
         return ;
     }
     pushdown(i,l,r);
     if(a<=mid) update(lson,l,mid,a,b);
     if(b>mid) update(rson,mid+,r,a,b);
     pushup(i);
 }

 int query(int i,int l,int r,int a,int b)
 {
     if(a<=l && r<=b)
         return segtree[i].sum;
     pushdown(i,l,r);
     int ans=;
     if(a<=mid) ans=(ans+query(lson,l,mid,a,b))%mod;
     if(mid<b) ans=(ans+query(rson,mid+,r,a,b))%mod;
     return ans;
 }

 int main()
 {
     init();
     int i,n,m,op,l,r;
     scanf("%d%d",&n,&m);
     for(i=;i<=n;i++) scanf("%d",a+i);
     build(,,n);
     while(m--)
     {
         scanf("%d%d%d",&op,&l,&r);
         if(op==) update(,,n,l,r);
         if(op==) printf("%d\n",query(,,n,l,r));
     }
     return ;
 }