HDU - 5015 233 Matrix（杨辉三角/前缀+矩阵快速幂）

233 Matrix

In our daily life we often use 233 to express our feelings. Actually, we may say 2333, 23333, or 233333 ... in the same meaning. And here is the question: Suppose we have a matrix called 233 matrix. In the first line, it would be 233, 2333, 23333... (it means a _0,1 = 233,a _0,2 = 2333,a _0,3 = 23333...) Besides, in 233 matrix, we got a_i,j = a _i-1,j +a _i,j-1( i,j ≠ 0). Now you have known a _1,0,a _2,0,...,a _n,0, could you tell me a _n,m in the 233 matrix?

InputThere are multiple test cases. Please process till EOF.

For each case, the first line contains two postive integers n,m(n ≤ 10,m ≤ 10 ⁹). The second line contains n integers, a _1,0,a _2,0,...,a _n,0(0 ≤ a _i,0 < 2 ³¹).OutputFor each case, output a _n,m mod 10000007.Sample Input

1 1
1
2 2
0 0
3 7
23 47 16

Sample Output

234
2799
72937

Hint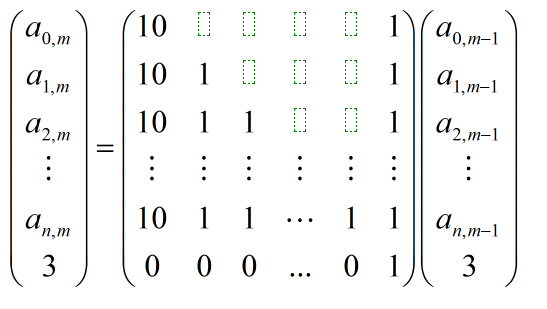

#include<bits/stdc++.h>
#define MAX 15
#define MOD 10000007
using namespace std;
typedef long long ll;
 
ll n,m;
struct mat{
    ll a[MAX][MAX];
};
 
mat operator *(mat x,mat y)
{
    mat ans;
    memset(ans.a,,sizeof(ans.a));
    for(int i=;i<=n+;i++){
        for(int j=;j<=n+;j++){
            for(int k=;k<=n+;k++){
                ans.a[i][j]+=x.a[i][k]*y.a[k][j]%MOD;
                ans.a[i][j]%=MOD;
            }
        }
    }
    return ans;
}
mat qMod(mat a,ll nn)
{
    mat t;
    memset(t.a,,sizeof(t.a));
    for(int i=;i<=n+;i++){
        t.a[i][]=;
        for(int j=;j<=i;j++){
            t.a[i][j]=;
        }
        t.a[i][n+]=;
    }
    t.a[n+][n+]=;
    while(nn){
        if(nn&) a=t*a;
        nn>>=;
        t=t*t;
    }
    return a;
}
int main()
{
    int t,i,j;
    while(~scanf("%I64d%I64d",&n,&m)){
        mat a;
        memset(a.a,,sizeof(a.a));
        a.a[][]=;
        for(i=;i<=n+;i++){
            scanf("%I64d",&a.a[i][]);
        }
        a.a[n+][]=;
        a=qMod(a,m);
        printf("%I64d\n",a.a[n+][]);
    }
    return ;
}