【bzoj3884】上帝与集合的正确用法 扩展欧拉定理

题目描述

根据一些书上的记载，上帝的一次失败的创世经历是这样的：

第一天， 上帝创造了一个世界的基本元素，称做“元”。

第二天， 上帝创造了一个新的元素，称作“α”。“α”被定义为“元”构成的集合。容易发现，一共有两种不同的“α”。

第三天， 上帝又创造了一个新的元素，称作“β”。“β”被定义为“α”构成的集合。容易发现，一共有四种不同的“β”。

第四天， 上帝创造了新的元素“γ”，“γ”被定义为“β”的集合。显然，一共会有16种不同的“γ”。

如果按照这样下去，上帝创造的第四种元素将会有65536种，第五种元素将会有2^65536种。这将会是一个天文数字。

然而，上帝并没有预料到元素种类数的增长是如此的迅速。他想要让世界的元素丰富起来，因此，日复一日，年复一年，他重复地创造着新的元素……

然而不久，当上帝创造出最后一种元素“θ”时，他发现这世界的元素实在是太多了，以致于世界的容量不足，无法承受。因此在这一天，上帝毁灭了世界。

至今，上帝仍记得那次失败的创世经历，现在他想问问你，他最后一次创造的元素“θ”一共有多少种？

上帝觉得这个数字可能过于巨大而无法表示出来，因此你只需要回答这个数对p取模后的值即可。

你可以认为上帝从“α”到“θ”一共创造了10^9次元素，或10^18次，或者干脆∞次。

一句话题意：

输入

接下来T行，每行一个正整数p，代表你需要取模的值

输出

T行，每行一个正整数，为答案对p取模后的值

样例输入

3
2
3
6

样例输出

0
1
4

---

题解

扩展欧拉定理

内容：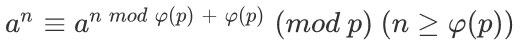

证明参考 https://zhuanlan.zhihu.com/p/24902174

这个定理不要求a和p互质，可以直接使用。

回到题目中，设a=2，n=2^2^...，由于有无穷个2，,所以有a^n mod p = a^(a^n mod phi(p) + phi(p)) mod p。

可以发现a^n mod p和a^n mod phi(p)是一样的，所以我们可以递归求解。

边界条件：当a^n mod p为定值时结束。我们可以知道当p=1时这个式子必然等于0，可以结束。

而且这样的方法时间复杂度是O(logp)的，参考 http://blog.csdn.net/popoqqq/article/details/43951401

这样加上快速幂就能求解了。

#include <cstdio>
#include <algorithm>
using namespace std;
typedef long long ll;
ll pow(ll y , ll p)
{
    ll x = 2 , ans = 1;
    while(y)
    {
        if(y & 1) ans = ans * x % p;
        x = x * x % p , y >>= 1;
    }
    return ans;
}
ll phi(ll x)
{
    ll i , ans = x;
    for(i = 2 ; i * i <= x ; i ++ )
    {
        if(x % i == 0)
        {
            ans = ans / i * (i - 1);
            while(x % i == 0) x /= i;
        }
    }
    if(x != 1) ans = ans / x * (x - 1);
    return ans;
}
ll cal(ll p)
{
    if(p == 1) return 0;
    ll t = phi(p);
    return pow(cal(t) + t , p);
}
int main()
{
    int T;
    ll p;
    scanf("%d" , &T);
    while(T -- ) scanf("%lld" , &p) , printf("%lld\n" , cal(p));
    return 0;
}