字典树Trie的使用

1. Trie树介绍

Trie，又称单词查找树、前缀树，是一种多叉树结构。如下图所示： 
上图是一棵Trie树，表示了关键字集合{“a”, “to”, “tea”, “ted”, “ten”, “i”, “in”, “inn”} 。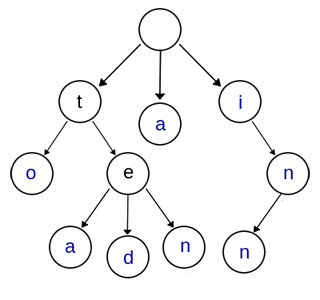 
 
与二叉查找树不同，键不是直接保存在节点中，而是由节点在树中的位置决定。一个节点的所有子孙都有相同的前缀，也就是这个节点对应的字符串，而根节点对应空字符串。

2. trie树性质：

1.根节点不包含字符，除根节点外的每一个节点都只包含一个字符。 
2.从根节点到某一节点，路径上经过的字符连接起来，为该节点对应的字符串。 
3.每个节点的所有子节点包含的字符都不相同。

3. trie树典型应用：

(1) 字符串检索 
查找某一个单词是否在树中。思路就是从根节点开始一个一个字符进行比较： 
如果沿路比较，发现不同的字符，则表示该字符串在集合中不存在。 
如果所有的字符全部比较完并且全部相同，还需判断最后一个节点的标志位（标记该节点是否代表字符串最后一个字符）。 
从而trie树可以设计为：

struct trie_node
{
bool isKey; // 标记该节点是否代表一个关键字
trie_node *children[]; // 各个子节点
}; 

(2) 词频统计

Trie树常被搜索引擎系统用于文本词频统计。 
思路：为了实现词频统计，我们可以修改节点结构，将ksKey用一个整型变量count来表示该节点为结尾的关键字的词频。对每一个关键字执行插入操作，若已存在，计数加1，若不存在，插入后count置1。 

struct trie_node
{
int count; // 记录该节点代表的单词的个数
trie_node *children[]; // 各个子节点
}; 

(3) 去除重复单词

建立字典树的过程就是给字符串去重的过程。 
(4) 字符串排序 
Trie树可以对大量字符串按字典序进行排序，思路也很简单：遍历一次所有关键字，将它们全部插入trie树，树的每个结点的所有儿子很显然地按照字母表排序，然后先序遍历输出Trie树中所有关键字即可。 
(5) 最长公共前缀 
查找N个单词的最长公共前缀 
(6) 前缀匹配: 
比如要找以“an”为前缀的字符串

4. trie树设计

为了计算英语字符串词频，trie树设计可以参考3.(2)词频统计。 
以上设计中因为是英文字符，父节点保存孩子节点时直接用一个数组children[26]来保存了孩子节点。这种方式最快，但是并不是所有节点都会有很多孩子，所以这种方式浪费的空间太多。可以用一个链表来代替数据。这样我们就可以省下不小的空间，但是缺点是搜索的时候需要遍历这个链表，增加了时间复杂度。如果存储汉字，可以把链表代替为map，这样既加快了速度，又不至于太浪费空间。

5. trie树优点：

(1) 查询快。对于长度为m的键值，最坏情况下只需花费O(m)的时间；而BST需要O(m log n)的时间。 虽然hash 表时间复杂度是O(1)，但是，哈希搜索的效率通常取决于 hash 函数的好坏，若一个坏的 hash 函数导致很多的冲突，效率并不一定比Trie树高。 
(2) 当存储大量字符串时，Trie耗费的空间较少。因为键值并非显式存储的，而是与其他键值共享子串。

6. trie树操作

(1) 初始化或清空：遍历Trie，删除所有节点，只保留根节点。 
(2) 插入字符串 
1. 设置当前节点为根节点，设置当前字符为插入字符串中的首个字符； 
2. 在当前节点的子节点上搜索当前字符，若存在，则将当前节点设为值为当前字符的子节点；否则新建一个值为当前字符的子节点，并将当前结点设置为新创建的节点。 
3. 将当前字符设置为串中的下个字符，若当前字符为0，则结束；否则转2. 
(3) 查找字符串 
搜索过程与插入操作类似，当字符找不到匹配时返回假；若全部字符都存在匹配，判断最终停留的节点是否为树叶，若是，则返回真，否则返回假。 
(4) 输出字符串词频 
(5) 删除字符串 
首先查找该字符串，边查询边将经过的节点压栈，若找不到，则返回假；否则依次判断栈顶节点是否为树叶，若是则删除该节点，否则返回真。 
(6) 输出字典树所有字符串 
(7) 计算所有字符串的词频总数（包含重复或不重复） 
(8) 计算字典树中所有单词的最长公共前缀及其长度

//使用字典树存储英文单词，使用的结构是26叉字典树。不区分单词的大小写
#include <cstring>
#include <iostream>

/* trie的节点类型 */
template <int Size> //Size为字符表的大小
struct trie_node
{
    int freq; //当前节点是否可以作为字符串的结尾,如果是freq>0,如果存在重复单词，freq表示该单词的词频
    int node; //子节点的个数
    trie_node *child[Size]; //指向子节点指针

    /* 构造函数 */
    trie_node() : freq(0), node(0) { memset(child, 0, sizeof(child)); }
};

/* trie */
template <int Size, typename Index> //Size为字符表的大小，Index为字符表的哈希函数
class trie
{
    public:
        /* 定义类型别名 */
        typedef trie_node<Size> node_type;
        typedef trie_node<Size>* link_type;

        /* 构造函数 */
        trie(Index i = Index()) : index(i){ }

        /* 析构函数 */
        ~trie() { clear(); }

        /* 清空 */
        void clear()
        {
            clear_node(root);
            for (int i = 0; i < Size; ++i)
                root.child[i] = 0;
        }

        /* 插入字符串 */
        template <typename Iterator>
            void insert(Iterator begin, Iterator end)
            {
                link_type cur = &root; //当前节点设置为根节点
                for (; begin != end; ++begin)
                {
                    if (!cur->child[index[*begin]]) //若当前字符找不到匹配，则新建节点
                    {
                        cur->child[index[*begin]] = new node_type;
                        ++cur->node; //当前节点的子节点数加一
                    }
                    cur = cur->child[index[*begin]]; //将当前节点设置为当前字符对应的子节点
                }
                (cur->freq)++; //设置存放最后一个字符的节点的可终止标志为真
            }

        /* 插入字符串，针对C风格字符串的重载版本 */
        void insert(const char *str)
        {
            insert(str, str + strlen(str));
        }

        /* 查找字符串，算法和插入类似 */
        template <typename Iterator>
            int getfreq(Iterator begin, Iterator end)
            {
                link_type cur = &root;
                for (; begin != end; ++begin)
                {
                    if (!cur->child[index[*begin]])
                        return false;
                    cur = cur->child[index[*begin]];
                }
                return cur->freq;
            }

        /* 查找字符串，针对C风格字符串的重载版本 */
        bool find(const char *str)
        {
            int freq =  getfreq(str, str + strlen(str));
            return freq > 0;
        }

        /* 查找字符串str的词频*/
        int getfreq(const char* str)
        {
            return getfreq(str,str + strlen(str));
        }

        /* 删除字符串 */
        template <typename Iterator>
            bool erase(Iterator begin, Iterator end)
            {
                bool result; //用于存放搜索结果
                erase_node(begin, end, root, result);
                return result;
            }

        /* 删除字符串，针对C风格字符串的重载版本 */
        bool erase(const char *str)
        {
            return erase(str, str + strlen(str));
        }

        /* 按字典序遍历单词树的所有单词 */
        template <typename Functor>
            void traverse( Functor execute = Functor())
            {
                char word[100] = {0};
                traverse_node(root, execute,word,0);
            }

        /*输出字典树单词的总个数，包含重复字符串*/
        int sizeAll()
        {
            sizeAll(root);
        }

        int sizeAll(node_type& cur)
        {
            int size = cur.freq;
            for(int i=0;i < Size; ++i)
            {
                if(cur.child[i] == 0)
                    continue;
                size += sizeAll(*cur.child[i]);
            }
            return size;
        }

        /*输出字典树单词的总个数，重复字符串按一个处理*/
        int sizeNoneRedundant()
        {
            sizeNoneRedundant(root);
        }

        int sizeNoneRedundant(node_type& cur)
        {
            int size = cur.freq>0?1:0;
            for(int i=0;i < Size;++i)
            {
                if(cur.child[i] == 0)
                    continue;
                size += sizeNoneRedundant(*cur.child[i]);
            }
            return size;
        }

        /*求字符串最长的公共前缀的长度*/
        int maxPrefix_length()
        {
            int length = maxPrefix_length(root);
            return length - 1;   //因为length包含了根节点，需要删除。
        }

        int maxPrefix_length(node_type& cur)
        {
            int length = 0;
            for(int i=0;i<Size;++i)
            {
                if(cur.child[i] != 0)
                {
                    int tmp = maxPrefix_length(*cur.child[i]);
                    if(tmp > length)
                    {
                        length = tmp;
                    }

                }
            }
            if(length > 0 || cur.node >1  || cur.freq >0 && cur.node>0)  //cur.node >1 处理"abcde"与"abcdf"这种情况；cur.freq>0 && cur.node>0处理"abcde"与"abcdef"这种情况
            {
                length++;
            }
            return length;

        }
        /*求字符串最长的最共前缀*/
        void maxPrefix(std::string& prefix)
        {
            maxPrefix(root,prefix);
            std::string word(prefix);
            int size = word.size();
            for(int i=0;i<size;++i)
                prefix[i] = word[size-1-i];
            prefix.erase(size-1);   //因为prefix包含了根节点字符，需要把它删除。

        }

        void maxPrefix(node_type& cur,std::string& prefix)
        {
            std::string word;
            int length =0 ;
            int k = 0;
            for(int i=0;i<Size;++i)
            {
                if(cur.child[i] != 0)
                {
                    maxPrefix(*cur.child[i],word);
                    if(word.size() > length)
                    {
                        length = word.size();
                        prefix.swap(word);
                        k = i;
                    }

                }
            }
            if(length > 0 || cur.node >1  || cur.freq >0 && cur.node>0)  //cur.node >1 处理"abcde"与"abcdf"这种情况；cur.freq>0 && cur.node>0处理"abcde"与"abcdef"这种情况
            {
                prefix.push_back(k + 'a');
            }
        }

    private:

        template<typename Functor>
            void traverse_node(node_type& cur, Functor execute,char* word,int index)
            {
                if(cur.freq)
                {
                    std::string str = word;
                    execute(str,cur.freq);
                }
                for(int i=0; i < Size; ++i)
                {
                    if(cur.child[i] != 0)
                    {
                        word[index++] = 'a' + i;
                        traverse_node(*cur.child[i],execute,word,index);
                        word[index] = 0;
                        index--;
                    }
                }

            }

        /* 清除某个节点的所有子节点 */
        void clear_node(node_type& cur)
        {
            for (int i = 0; i < Size; ++i)
            {
                if (cur.child[i] == 0) continue;
                clear_node(*cur.child[i]);
                delete cur.child[i];
                cur.child[i] = 0;
                if (--cur.node == 0) break;
            }
        }

        /* 边搜索边删除冗余节点，返回值用于向其父节点声明是否该删除该节点 */
        template <typename Iterator>
            bool erase_node(Iterator begin, Iterator end, node_type &cur, bool &result)
            {
                if (begin == end) //当到达字符串结尾：递归的终止条件
                {
                    result = (cur.freq > 0);   //如果当前节点的频率>0,则当前节点可以作为终止字符，那么结果为真
                    if(cur.freq)
                        cur.freq --;            //如果当前节点为终止字符，词频减一
                    return cur.freq == 0 && cur.node == 0;    //若该节点为树叶，那么通知其父节点删除它
                }
                //当无法匹配当前字符时，将结果设为假并返回假，即通知其父节点不要删除它
                if (cur.child[index[*begin]] == 0) return result = false;
                //判断是否应该删除该子节点
                else if (erase_node((++begin)--, end, *(cur.child[index[*begin]]), result))
                {
                    delete cur.child[index[*begin]]; //删除该子节点
                    cur.child[index[*begin]] = 0; //子节点数减一
                    //若当前节点为树叶，那么通知其父节点删除它
                    if (--cur.node == 0 && cur.freq == 0) return true;
                }
                return false; //其他情况都返回假
            }

        /* 根节点 */
        node_type root;

        /* 将字符转换为索引的转换表或函数对象 */
        Index index;
};

//index function object
class IndexClass
{
    public:
        int operator[](const char key)
        {
            if(key>='a' && key <= 'z')
                return key - 'a';
            else if(key >= 'A' && key <= 'Z')
                return key - 'A';
        }
};

class StringExe
{
    public:
        void operator()(std::string& str,int freq)
        {
            std::cout<<str<<":"<<freq<<std::endl;
        }
};
int main()
{
    trie<26,IndexClass> t;
    t.insert("tree");
    t.insert("tree");
    t.insert("tea");
    t.insert("A");
    t.insert("BABCDEGG");
    t.insert("BABCDEFG");

    t.traverse<StringExe>();

    int sizeall = t.sizeAll();
    std::cout<<"sizeAll:"<<sizeall<<std::endl;

    int size = t.sizeNoneRedundant();
    std::cout<<"size:"<<size<<std::endl;

    std::string prefix;
    int deep = t.maxPrefix_length();
    t.maxPrefix(prefix);
    std::cout<<"deep:"<<deep<<" prefix:"<<prefix<<std::endl;

    if(t.find("tree"))
        std::cout<<"find tree"<<std::endl;
    else
        std::cout<<"not find tree"<<std::endl;

    int freq = t.getfreq("tree");
    std::cout<<"tree freq:"<<freq<<std::endl;

    if(t.erase("tree"))
        std::cout<<"delete tree"<<std::endl;
    else
        std::cout<<"not find tree"<<std::endl;

    freq = t.getfreq("tree");
    std::cout<<"tree freq:"<<freq<<std::endl;

    if(t.erase("tree"))
        std::cout<<"delete tree"<<std::endl;
    else
        std::cout<<"not find tree"<<std::endl;

    if(t.erase("tree"))
        std::cout<<"delete tree"<<std::endl;
    else
        std::cout<<"not find tree"<<std::endl;

    sizeall = t.sizeAll();
    std::cout<<"sizeAll:"<<sizeall<<std::endl;

    size = t.sizeNoneRedundant();
    std::cout<<"size:"<<size<<std::endl;

    if(t.find("tre"))
        std::cout<<"find tre"<<std::endl;
    else
        std::cout<<"not find tre"<<std::endl;

    t.traverse<StringExe>();

    return 0;
}