Codeforces 762D Maximum path 动态规划

Codeforces 762D

题目大意:

给定一个\(3*n(n \leq 10^5)\)的矩形，从左上角出发到右下角，规定每个格子只能经过一遍。经过一个格子会获得格子中的权值。每个格子的权值\(a_{ij}\)满足\(-10^9 \leq a_{ij} \leq 10^9\).最大化收益

题解:

乍一看，好麻烦！

最主要的是因为他能够往回走.

但是我们画图可以发现:每次往回走一定不用超过1次.

也就是说，最多只能走成这样



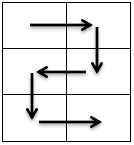
而不会走成这样



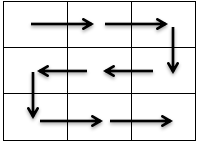
因为下图的走法一定可以用上图组合，并且

由于只用3行的特性，每次向回走实际上是取走了所有的数.

所以我们只采用上图方式得出来的答案一定最优

所以我们O(n)线性递推即可

设\(f[i][j]\)为到达第i列第j行的最大收益

方程比较多，就不写了，自己看代码吧。

#include <cstdio>
#include <cstring>
#include <algorithm>
using namespace std;
typedef long long ll;
template<typename T>inline void read(T &x){
	x=0;char ch;bool flag = false;
	while(ch=getchar(),ch<'!');if(ch == '-') ch=getchar(),flag = true;
	while(x=10*x+ch-'0',ch=getchar(),ch>'!');if(flag) x=-x;
}
template<typename T>inline T cat_max(const T &a,const T &b){return a>b ? a:b;}
template<typename T>inline T cat_min(const T &a,const T &b){return a<b ? a:b;}
const int maxn = 100010;
ll w[maxn][6],f[maxn][6],g[maxn][6];
int main(){
	int n;read(n);
	for(int i=1;i<=n;++i) read(w[i][1]);
	for(int i=1;i<=n;++i) read(w[i][2]);
	for(int i=1;i<=n;++i) read(w[i][3]);
	f[1][1] = w[1][1];
	f[1][2] = w[1][1] + w[1][2];
	f[1][3] = w[1][1] + w[1][2] + w[1][3];
	g[1][1] = w[1][1];g[1][2] = w[1][2];g[1][3] = w[1][3];
	for(int i=2;i<=n;++i){
		f[i][1] = g[i][1] = f[i-1][1] + w[i][1];
		f[i][2] = g[i][2] = f[i-1][2] + w[i][2];
		f[i][3] = g[i][3] = f[i-1][3] + w[i][3];
		f[i][1] = cat_max(f[i][1],g[i][2] + w[i][1]);
		f[i][1] = cat_max(f[i][1],g[i][3] + w[i][2] + w[i][1]);
		f[i][2] = cat_max(f[i][2],g[i][1] + w[i][2]);
		f[i][2] = cat_max(f[i][2],g[i][3] + w[i][2]);
		f[i][3] = cat_max(f[i][3],g[i][2] + w[i][3]);
		f[i][3] = cat_max(f[i][3],g[i][1] + w[i][2] + w[i][3]);
		f[i][1] = cat_max(f[i][1],g[i-1][3] + w[i][3] + w[i][2] + w[i-1][2] + w[i-1][1] + w[i][1]);
		f[i][3] = cat_max(f[i][3],g[i-1][1] + w[i][1] + w[i][2] + w[i-1][2] + w[i-1][3] + w[i][3]);
	}
	printf("%I64d",f[n][3]);
	getchar();getchar();
	return 0;
}