本系列笔记内容参考来源为李航《统计学习方法》

EM算法是一种迭代算法，用于含有隐变量的概率模型参数的极大似然估计或极大后验概率估计。迭代由

（1）E步：求期望

（2）M步：求极大

组成，称为期望极大算法。

EM算法引入

EM算法是通过不断求解下界的极大化逼近求解对数似然函数极大化的算法。

EM在监督学习中的应用

收敛性

EM算法在高斯混合模型学习中的应用

高斯混合模型

高斯混合模型参数估计的EM算法

EM算法的推广

EM算法还可解释为F函数的极大-极大算法，基于这个解释有若干变形与推广。

首先引入F函数的概念

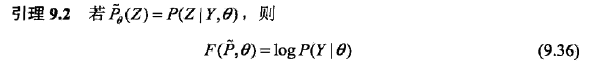
《统计学习方法》笔记九 EM算法及其推广的更多相关文章

  1. EM算法及其推广

    概述 EM算法是一种迭代算法,用于含有隐变量(hidden variable)的概率模型参数的极大似然估计,或极大后验概率估计. EM算法的每次迭代由两步组成:E步,求期望(expectation): ...

  2. 统计学习方法笔记--EM算法--三硬币例子补充

    本文,意在说明<统计学习方法>第九章EM算法的三硬币例子,公式(9.5-9.6如何而来) 下面是(公式9.5-9.8)的说明, 本人水平有限,怀着分享学习的态度发表此文,欢迎大家批评,交流 ...

  3. python机器学习笔记：EM算法

    EM算法也称期望最大化(Expectation-Maximum,简称EM)算法,它是一个基础算法,是很多机器学习领域的基础,比如隐式马尔科夫算法(HMM),LDA主题模型的变分推断算法等等.本文对于E ...

  4. GMM高斯混合模型学习笔记（EM算法求解）

    提出混合模型主要是为了能更好地近似一些较复杂的样本分布,通过不断添加component个数,能够随意地逼近不论什么连续的概率分布.所以我们觉得不论什么样本分布都能够用混合模型来建模.由于高斯函数具有一 ...

  5. 统计学习方法笔记 -- KNN

    K近邻法(K-nearest neighbor,k-NN),这里只讨论基于knn的分类问题,1968年由Cover和Hart提出,属于判别模型 K近邻法不具有显式的学习过程,算法比较简单,每次分类都是 ...

  6. EM算法及其推广的要点

    1.EM算法是含有隐变量的变量的概率模型极大似然估计或极大后验概率估计的迭代算法,含有隐变量的概率模型的数据表示为$P(Y,Z|\theta)$.这里,$Y$是观测变量的数据,$Z$是隐变量的数据,$ ...

  7. 【机器学习笔记】EM算法及其应用

    极大似然估计 考虑一个高斯分布\(p(\mathbf{x}\mid{\theta})\),其中\(\theta=(\mu,\Sigma)\).样本集\(X=\{x_1,...,x_N\}\)中每个样本 ...

  8. 统计学习方法笔记（KNN）

    k近邻法(k-nearest neighbor,k-NN) 输入:实例的特征向量,对应于特征空间的点:输出:实例的类别,可以取多类. 分类时,根据其k个最近邻的训练实例的类别,通过多数表决等方式进行预 ...

  9. 统计学习方法笔记 -- Boosting方法

    AdaBoost算法 基本思想是,对于一个复杂的问题,单独用一个分类算法判断比较困难,那么我们就用一组分类器来进行综合判断,得到结果,"三个臭皮匠顶一个诸葛亮" 专业的说法, 强可 ...

随机推荐

  1. tomcat正常启动，但是java项目没有启动原因

    右键项目,选择properties,查看该属性配置的是否正确

  2. CMD help

    ASSOC 显示或修改文件扩展名关联. ATTRIB 显示或更改文件属性. BREAK 设置或清除扩展式 CTRL+C 检查. BCDEDIT 设置启动数据库中的属性以控制启动加载. CACLS 显示 ...

  3. 51Nod - 1821：最优集合 （求第一个不能被表示为多个数的和的数）（不错的动脑题）

    一个集合S的优美值定义为:最大的x,满足对于任意i∈1,x1,x,都存在一个S的子集S',使得S'中元素之和为i. 给定n个集合,对于每一次询问,指定一个集合S1和一个集合S2,以及一个数k,要求选择 ...

  4. 「LOJ#10043」「一本通 2.2 例 1」剪花布条 （KMP

    题目描述 原题来自:HDU 2087 一块花布条,里面有些图案,另有一块直接可用的小饰条,里面也有一些图案.对于给定的花布条和小饰条,计算一下能从花布条中尽可能剪出几块小饰条来呢? 输入格式 输入数据 ...

  5. [SHOI 2007] 善意的投票

    [题目链接] https://www.lydsy.com/JudgeOnline/problem.php?id=1934 [算法] 首先 , 选择睡觉的人和不选择睡觉的人构成两个集合 这启发我们用最小 ...

  6. PHP mysql_fetch_array与mysql_fetch_row的区别

    如果你的表里面有字段a,b,c那么你用mysql_fetch_row() 就返回array(1=>a的值,2=>b的值,3=>c的值)这个时候你读数组的话,只能这样写$array[1 ...

  7. HDU2896(AC自动机入门题)

    病毒侵袭 Time Limit:1000MS     Memory Limit:32768KB   Description 当太阳的光辉逐渐被月亮遮蔽,世界失去了光明,大地迎来最黑暗的时刻....在这 ...

  8. why ftp服务器采用多进程模式

    为什么没有采用多线程或者IO复用,原因是在多线程或IO复用的情况下,当前目录是共享的,无法根据每一个连接来拥有自己的当前目录. 多进程模式下,一个连接拥有2个进程,一个是nobody进程,一个是服务进 ...

  9. JS获取元素的offsetTop,offsetLeft等相关属性

    1. obj.clientWidth //获取元素的宽度 obj.clientHeight //元素的高度 obj.offsetLeft //元素相对于父元素的left obj.offsetTop / ...

  10. 算法导论17：摊还分析学习笔记(KMP复杂度证明)

    在摊还分析中,通过求数据结构的一系列的操作的平均时间,来评价操作的代价.这样,即使这些操作中的某个单一操作的代价很高,也可以证明平均代价很低.摊还分析不涉及概率,它可以保证最坏情况下每个操作的平均性能 ...