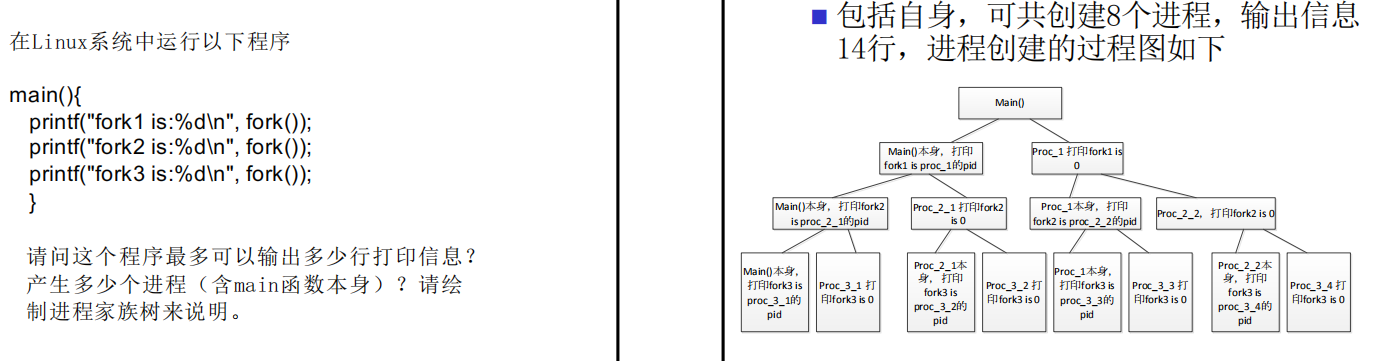
Linux中fork函数的例子的更多相关文章

  1. 【转】linux 中fork()函数详解

    在看多线程的时候看到了这个函数,于是学习了下,下面文章写的通俗易懂,于是就开心的看完了,最后还是很愉快的算出了他最后一个问题. linux 中fork()函数详解 一.fork入门知识 一个进程,包括 ...

  2. Linux中fork()函数详解（转载）

    linux中fork()函数详解 一.fork入门知识 一个进程,包括代码.数据和分配给进程的资源.fork()函数通过系统调用创建一个与原来进程几乎完全相同的进程,也就是两个进程可以做完全相同的事, ...

  3. linux中fork()函数

    man fork: FORK() Linux Programmer's Manual FORK(2) NAME fork - create a child process SYNOPSIS #incl ...

  4. linux中fork函数详解(转)

    add by zhj: 在Linux,创建进程是用fork(),它其实就是拷贝父进程的数据段和其它数据,这相当于C函数调用中的值传递,这是 此后两者的修改都互不影响.因为两者的数据虽相同,但却在不同的 ...

  5. Linux中fork()函数详解（转）

    一.fork入门知识 一个进程,包括代码.数据和分配给进程的资源.fork()函数通过系统调用创建一个与原来进程几乎完全相同的进程,也就是两个进程可以做完全相同的事,但如果初始参数或者传入的变量不同, ...

  6. Linux中fork()函数详解

    一个进程,包括代码.数据和分配给进程的资源.fork()函数通过系统调用创建一个与原来进程几乎完全相同的进程, 也就是两个进程可以做完全相同的事,但如果初始参数或者传入的变量不同,两个进程也可以做不同 ...

  7. Linux中fork()函数的底层实现【转】

    转自:http://blog.csdn.net/duoru_xiong/article/details/76358812 1. fork(),vfork(),clone()的区别 这三个系统调用的底层 ...

  8. Linux中fork的秘密

    linux中fork()函数详解         一.fork入门知识 一个进程,包括代码.数据和分配给进程的资源.fork()函数通过系统调用创建一个与原来进程几乎完全相同的进程,也就是两个进程可以 ...

  9. Linux环境fork()函数详解

    Linux环境fork()函数详解 引言 先来看一段代码吧, 1 #include <sys/types.h> 2 #include <unistd.h> 3 #include ...

随机推荐

  1. python之文件的读写（2）

    小R昨天因为在研究weblogic的漏洞就没来得及学习python(好吧,这都是借口,懒了,大家可不能像我这样.要坚持每天都学).   这个进度是有点慢呀.哎呀,没事没事,我还年轻,才20岁.  哈哈 ...

  2. E20181120-hm

    checkerboard n. 西洋跳棋盘; checker n. 方格图案;

  3. Solve Tree Problems Recursively

    "Top-down" Solution Here is the pseudocode for the recursion function maximum_depth(root, ...

  4. lightoj 1076 【二分找满足条件的最左】

    #include <bits/stdc++.h> using namespace std; typedef long long LL; typedef unsigned long long ...

  5. NGUI研究院之UISprite和UITexture浅谈

    NGUI的三大组件,UILabel.UISprite.UITexture,它们三个同时都继承UIWidget.先回到一个很郁闷的话题上,到底是优化DrawCall还是优化内存. UISprite : ...

  6. [3dmax教程] 人物+骨骼+蒙皮+动画教程

    人物+骨骼+蒙皮+动画完整教程选准备好一个人,做人的方法我在这里就不做了,大家可以学都用poser来做一个.  在大腿里建立4根骨骼! 在前视图中移动如图所示位置! 做一段简单的骨骼向前伸的动画,做4 ...

  7. word2vec改进之Negative Sampling

    训练网络时往往会对全部的神经元参数进行微调,从而让训练结果更加准确.但在这个网络中,训练参数很多,每次微调上百万的数据是很浪费计算资源的.那么Negative Sampling方法可以通过每次调整很小 ...

  8. 用EnumMap代替序数索引

    用EnumMap代替序数索引   有时候,会见到利用ordinal方法来索引数组的代码.例如下面这个简化的类,表示一种烹饪用的香草: public class Herb { public enum T ...

  9. Centos7安装与配置domain模式wildfly（默认配置）

    (1)安装与配置JDK8 1)使用wget下载JDK8: wget --no-check-certificate --no-cookies --header "Cookie: oraclel ...

  10. [题解]（折半搜索/高斯消元枚举自由元）BZOJ_1770_Lights

    状压,时间空间都不行,如果每次搜索一半就可以省下很多空间,用map记下每种状态的答案,最后再把两次的答案合并 然而正解是高斯消元解异或方程组,最后搜索自由元 #include<iostream& ...