浅谈PCA

最近在回顾PCA方面的知识，发现对于之前的很多东西有了新的理解，下面和大家分享下我的一些个人的理解

1.我们为什么要用PCA，它能解决我什么问题？

　　PCA（Principal Component Analysis），主成成分分析，常用于高维数据的降维。在企业级环境中，最终用于模型训练的数据集往往维度很高，占用内存空间更大。PCA的出现，能保证尽量保留数据更完整信息的同时，将数据降低到更低的维度，这样不仅占用内存空间更小，模型训练速度也明显加快！ （这里的模型训练的速度的加快是   降维之前训练所用的时间  对比 降维所用的时间 + 降维之后训练所用的时间 ）

2.PCA的理论分析

　　PCA的目标:

　　　　　　　　2.1：将原始数据集通过降维的方式，在新的坐标系下表示，新的坐标系的维度远低于原始维度。

　　　　　　　　2.2：在新的坐标系下的表示应尽量保留相对完整的信息。

　　对于2.2我们知道，完整的信息指的是数据间的差异。例如我们在做模型训练的时候，往往希望训练数据的分布是涵盖了所有的情况一样。我们用方差来衡量数据间的离散程度，这也是新坐标下的衡量指标，我们要找到这样的一组坐标系，使得原始数据在新坐标系下的方差最大。同时我们考虑到，如果从高维降低到一维，上面的论述是没有问题的，如果降低到k维度(1<k<n)，那么每次都去寻找使方差最大的那条坐标轴得到的结果是k条结果是重合的。得到的新的坐标轴应该是在已得到坐标轴的基础之上，对原有数据未展示的信息做补充(为了最大化展示原有信息)，所以我们期望得到的一组坐标系之间的坐标轴是两两互不相关的。

3.准备工作

　　进行降维之前，让我们来做些准备工作。首先对数据进行0均值归一化，之后再做标准化处理。使得所有数据在同一量纲。

4.数学推导

　　

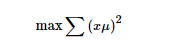
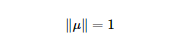
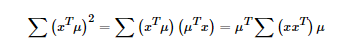
上式中的μ为空间中的一个向量，x为经过特征工程处理过后的矩阵。第一个式子为我们的目标函数，第二个为最优解的约束，问题为在约束空间内求最优解的问题，用拉格朗日乘子来求解。

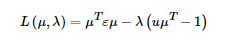　　　　得到下面的结果：

　　　　

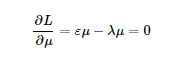
　　　　其中我们使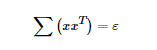，为协方差矩阵。所以我们知道μ就是e的主特征向量。（关于特征向量和特征值的一些概念，可以参靠一些资料来复习下）

　　　　我们的原始问题在此刻即转变为求e矩阵的TOPk个特征值对应的k个特征向量的问题

5.选几个？

对应最终的特征向量，我们选取几个，最终数据降低到几维度，那么，我们要怎么选取？

　　　　

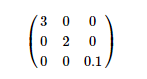
　　　　假设上式为降维后对应的特征向量，那么根据特征值占比来选择最终保留的维度，即如果降低到1维  此时的特征值占比为(3/3+2+0.1)，如果降低到二维度，此时的特征值占比为(3+2/3+2+0.1)

　　　　如果要求信息量保留95%，那么根据特征值占比与目标值做比较，达到要求即可。

6.代码的实现

　　　　

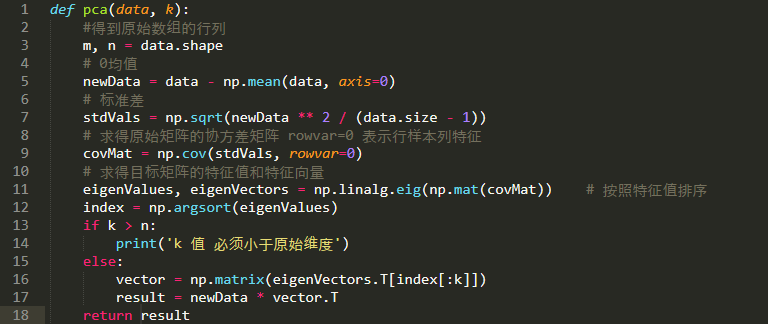
　　　　上图代码是根据降低到最终的维度来做的，感兴趣的同学可以实现一下按照保留信息量来实现

　　　　主播水平有限，如果有错的地方，欢迎大家批评指正！

参考资料：吴恩达机器学习公开课

　　　　　马同学高等数学公众号