剑指offer-第四章解决面试题的思路（包含min函数的栈）

题目：定义栈的数据结构，请在该类型中实现一个能够得到栈的最小元素的min函数，在该栈中，调用min,push及pop的时间复杂度都是O（1）

思路：定义两个栈分别为dataStack和minStack,dataStack用来存放要放入栈中的数据，而minStack用来存放dataStack中的对应时刻的最小值。

抽象问题具体化：如下图所示：

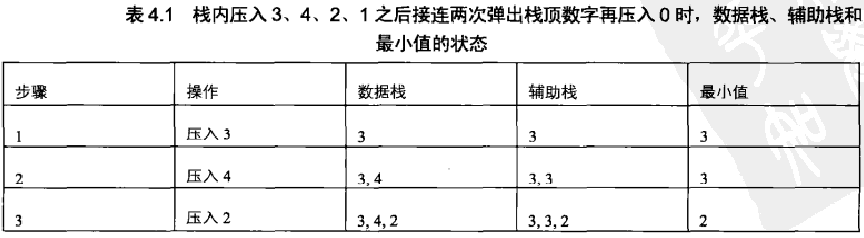
C++代码：

#include <stack>
#include <assert.h>
#include <stddef.h>  

template <typename T> class StackWithMin
{
public:
    StackWithMin(void) {}
    virtual ~StackWithMin(void) {}  

    T& top(void);
    const T& top(void) const;  

    void push(const T& value);
    void pop(void);  

    const T& min(void) const;  

    bool empty() const;
    size_t size() const;  

private:
    std::stack<T>   m_data;     // 数据栈，存放栈的所有元素
    std::stack<T>   m_min;      // 辅助栈，存放栈的最小元素
};  

template <typename T> void StackWithMin<T>::push(const T& value)
{
    // 把新元素添加到辅助栈
    m_data.push(value);  

    // 当新元素比之前的最小元素小时，把新元素插入辅助栈里；
    // 否则把之前的最小元素重复插入辅助栈里
    if(m_min.size() ==  || value < m_min.top())
        m_min.push(value);
    else
        m_min.push(m_min.top());
}  

template <typename T> void StackWithMin<T>::pop()
{
    //assert的作用是现计算表达式 expression ，如果其值为假（即为0），那么它先向stderr打印一条出错信息，然后通过调用 abort 来终止程序运行。
    assert(m_data.size() >  && m_min.size() > );
    m_data.pop();
    m_min.pop();
}  

template <typename T> const T& StackWithMin<T>::min() const
{
    assert(m_data.size() >  && m_min.size() > );  

    return m_min.top();
}  

template <typename T> T& StackWithMin<T>::top()
{
    return m_data.top();
}  

template <typename T> const T& StackWithMin<T>::top() const
{
    return m_data.top();
}  

template <typename T> bool StackWithMin<T>::empty() const
{
    return m_data.empty();
}  

template <typename T> size_t StackWithMin<T>::size() const
{
    return m_data.size();
}
void Test(char* testName, const StackWithMin<int>& stack, int expected)
{
    if(testName != NULL)
        printf("%s begins: ", testName);  

    if(stack.min() == expected)
        printf("Passed.\n");
    else
        printf("Failed.\n");
}  

int main()
{
    StackWithMin<int> stack;  

    stack.push();
    Test("Test1", stack, );  

    stack.push();
    Test("Test2", stack, );  

    stack.push();
    Test("Test3", stack, );  

    stack.push();
    Test("Test4", stack, );  

    stack.pop();
    Test("Test5", stack, );  

    stack.pop();
    Test("Test6", stack, );  

    stack.pop();
    Test("Test7", stack, );  

    stack.push();
    Test("Test8", stack, );  

    return ;
}  

Java代码：

import java.util.Stack;

/**
 * 实现包含min函数的栈
 * @author DHC
 * @param <T>
 */
public class MinInStack<T> {

    public static void main(String[] args) {
        MinInStack<Integer> newStack = new MinInStack<Integer>();
        newStack.push(4);
        System.out.println(newStack.min());
        newStack.push(6);
        System.out.println(newStack.min());
        newStack.push(2);
        System.out.println(newStack.min());
        newStack.push(5);
        System.out.println(newStack.min());
        newStack.pop();
        System.out.println(newStack.min());
        newStack.pop();
        System.out.println(newStack.min());
        newStack.push(1);
        System.out.println(newStack.min());
    }

    public Stack<T> dataStack = new Stack<T>();

    public Stack<T> minStack = new Stack<T>();

    public void pop() {
       if(dataStack.size()>0&&minStack.size()>0)
       {
            dataStack.pop();
            minStack.pop();
       }
    }

    public void push(T item) {
        dataStack.push(item);
        if(minStack.size()==0||compare(minStack.peek(),item))
        {
            minStack.push(item);
        }
        else
            minStack.push(minStack.peek());
    }

    public T peek() {

        return dataStack.peek();
    }

    public T min() {
       return minStack.peek();
    }

    public boolean isEmpty() {
        return dataStack.isEmpty();
    }
    public int size(){
        return dataStack.size();
    }

    /**
     * 泛型元素的比较方法
     * @param minData
     * @param item
     * @return true 代表当前元素小于之前的最小元素
     */

    public boolean compare(T minData, T item) {
        // 这儿不同的泛型类型可以用不同的方式实现
        // 如果写成通用代码泛型之间应该肿么比较大小呢？是不是可以让泛型都继承某一接口呢？
        int a = (Integer) minData;
        int b = (Integer) item;
        if(a > b) {
            return true;
        } else {
            return false;
        }
    }
}