Louvain 算法原理

Louvain算法是一种基于图数据的社区发现算法，算法的优化目标为最大化整个数据的模块度，模块度的计算如下：

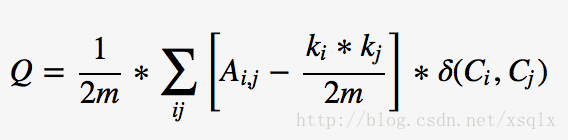
其中m为图中边的总数量，k_i表示所有指向节点i的连边权重之和，k_j同理。A_{i,j} 表示节点i，j之间的连边权重。有一点要搞清楚，模块度的概念不是Louvain算法发明的，而Louvain算法只是一种优化关系图模块度目标的一种实现而已。

Louvain算法的两步迭代设计：
最开始，每个原始节点都看成一个独立的社区，社区内的连边权重为0.
       算法扫描数据中的所有节点，针对每个节点遍历该节点的所有邻居节点，衡量把该节点加入其邻居节点所在的社区所带来的模块度的收益。并选择对应最大收益的邻居节点，加入其所在的社区。这一过程化重复进行指导每一个节点的社区归属都不在发生变化。
       对步骤1中形成的社区进行折叠，把每个社区折叠成一个单点，分别计算这些新生成的“社区点”之间的连边权重，以及社区内的所有点之间的连边权重之和。用于下一轮的步骤1。
该算法的最大优势就是速度很快，步骤1的每次迭代的时间复杂度为O(N)，N为输入数据中的边的数量。步骤2 的时间复杂度为O(M + N)， M为本轮迭代中点的个数。
迭代过程：

1， 假设我们最开始有5个点，互相之间存在一定的关系（至于什么关系，先不管），如下：

2. 假设在进过了步骤1的充分迭代之后发现节点2，应该加入到节点1所在的社区（最开始每个点都是一个社区，而自己就是这个社区的代表），新的社区由节点1代表，如下：

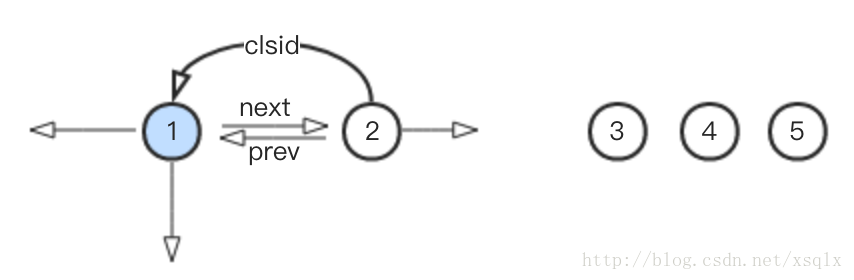
此时节点3，4，5之间以及与节点1，2之间没有任何归属关系。

3. 此时应该执行步骤2，将节点1，2组合成的新社区进行折叠，折叠之后的社区看成一个单点，用节点1来代表，如下：

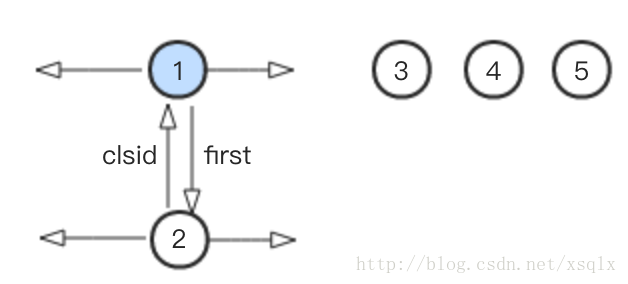
此时数据中共有4个节点（或者说4个社区），其中一个社区包含了两个节点，而社区3，4，5都只包含一个节点，即他们自己。

4. 重新执行步骤1，对社区1，3，4，5进行扫描，假设在充分迭代之后节点5，4，3分别先后都加入了节点1所在的社区，如下：

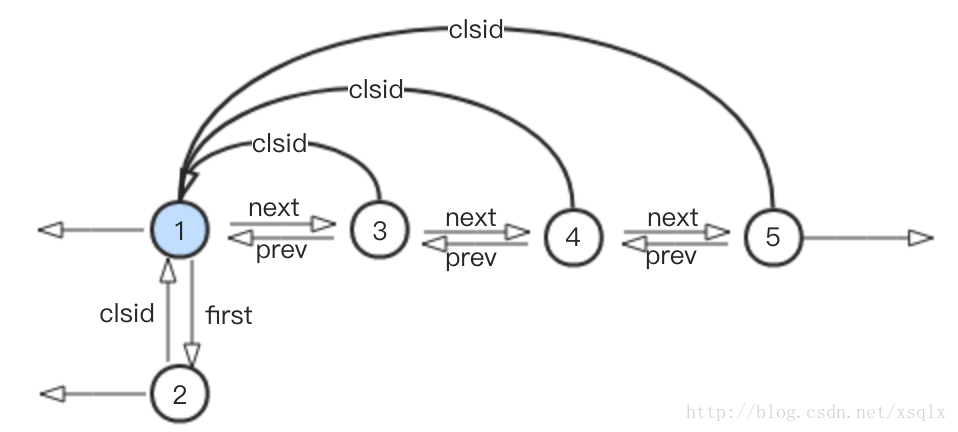
5. 进行步骤2，对新生成的社区进行折叠，新折叠而成的社区看成一个单点，由节点1代表，结构如下：

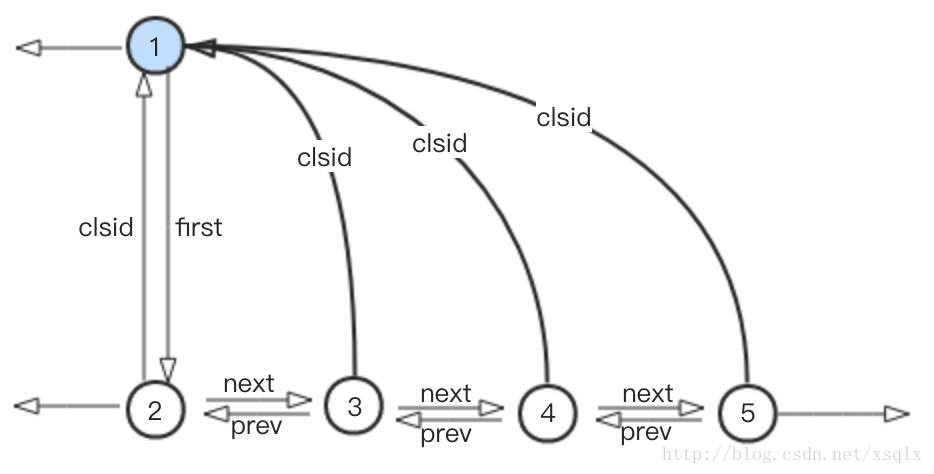
此时由于整个数据中只剩下1个社区，即由节点1代表的社区。再进行步骤1时不会有任何一个节点的社区归属发生变化，此时也就不需要再执行步骤2，至此， 迭代结束。

转自: https://blog.csdn.net/xsqlx/article/details/79078867