POJ1003 – Hangover (基础)

Hangover

 

Description

How far can you make a stack of cards overhang a table? If you have one card, you can create a maximum overhang of half a card length. (We're assuming that the cards must be perpendicular to the table.) With two cards you can make the top card overhang the bottom one by half a card length, and the bottom one overhang the table by a third of a card length, for a total maximum overhang of 1/2 + 1/3 = 5/6 card lengths. In general you can make n cards overhang by 1/2 + 1/3 + 1/4 + ... + 1/(n + 1) card lengths, where the top card overhangs the second by 1/2, the second overhangs tha third by 1/3, the third overhangs the fourth by 1/4, etc., and the bottom card overhangs the table by 1/(n + 1). This is illustrated in the figure below.

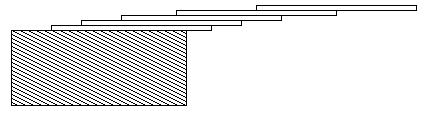
Input

The input consists of one or more test cases, followed by a line containing the number 0.00 that signals the end of the input. Each test case is a single line containing a positive floating-point number c whose value is at least 0.01 and at most 5.20; c will contain exactly three digits.

Output

For each test case, output the minimum number of cards necessary to achieve an overhang of at least c card lengths. Use the exact output format shown in the examples.

Sample Input

1.00
3.71
0.04
5.19
0.00

Sample Output

3 card(s)
61 card(s)
1 card(s)
273 card(s)

Source

Mid-Central USA 2001

 

  根据题意可建立以下数学模型：
     令 ∑(1/n) >= c
     其中 n∈[2, ∞), c∈[0.01, 5.20]且其精度含小数在内最多3个数字
     给定c 求 n （若c在范围外，则不求解）
 
    分析：
     本质就是变种的调和数列求和（数列中缺少1）
     但调和数列是发散的，不存在准确的求和公式，只有近似公式：
      调和数列 ∑(1/n) ~ ln(n+1) + R
      其中 n∈[1, ∞), R为欧拉常数(R = 0.5772156649...)
 
     但近似公式只有在n非常大的时候误差才可以忽略不计，
     当n很小时，对本题而言误差是不可接受的。
 
     因此本题用常规解法即可
     （由于前n项和是固定的，用打表法也可, 不过题目考核范围较小，打表意义也不大） 

#include <iostream>
using namespace std;
 
/*
 * 根据调和数列的和值反求项数
 * @param sum 目标和值
 * return 调和数列项数
 */
int harmonicSeries(double sum);
 
int main(void) {
    double sum = 0.0;
    while(true) {
        cin >> sum;
        if(sum < 0.01 || sum > 5.20) {
            break;
        }
 
        int n = harmonicSeries(sum);
        cout << n << " card(s)" << endl;
    }
    return ;
}
 
int harmonicSeries(double sum) {
    int n = ;
    double curSum = 0.0;
    while(curSum < sum) {
        curSum += (1.0 / n++);
    }
    return n - ;   // n从2开始因此项数-1, 最后一次求和多了一次n++也要-1， 因此共-2
}