光流法详解之一(LK光流）

Lucas–Kanade光流算法是一种两帧差分的光流估计算法。它由Bruce D. Lucas 和 Takeo Kanade提出 [1]。

LK光流法有三个假设条件：

1. 亮度恒定：一个像素点随着时间的变化，其亮度值（像素灰度值）是恒定不变的。这是光流法的基本设定。所有光流法都必须满足。

2. 小运动： 时间的变化不会引起位置的剧烈变化。这样才能利用相邻帧之间的位置变化引起的灰度值变化，去求取灰度对位置的偏导数。所有光流法必须满足。

3. 空间一致：即前一帧中相邻像素点在后一帧中也是相邻的。这是LK光流法独有的假定。因为为了求取x,y方向的速度，需要建立多个方程联立求解。而空间一致假设就可以利用邻域n个像素点来建立n个方程。

LK光流算法原理的数学推导：

假设前一帧时间为t， 后一帧时间为t+δt。则前一帧I的像素点I(x, y, z, t)在后一帧中的位置为I(x+δx, y+δy, z+δz, t+δt )。

① 根据亮度恒定假设：

　　

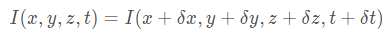
② 根据小运动假设， 将上式右侧用泰勒级数展开：

　　

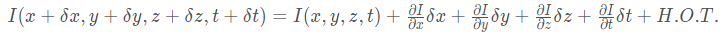
　　H.O.T是泰勒级数展开式的高阶项，小运动情况下可以 忽略为0.

③ 根据上面两个公式可以得到：

　　

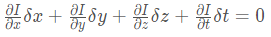
　　或者下面的公式：

　　

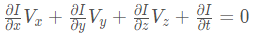
而对于二维图像而言，只需要考虑x, y, t即可，其中Ix，Iy  It分别为图像在(x, y, t)方向的差分，写为如下形式：

　　

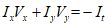
④ 现在有两个未知数，只有一个方程。因此用到第三个假设：即空间一致性假设，LK算法是利用3x3窗口内的9个像素点建立9个方程。简写为下面的形式：　　

　　

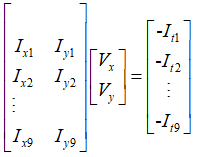
　　写成矩阵形式：

　　

　　当然两个未知数，9个方程，这是一个超定问题，采用最小二乘法解决：

　　

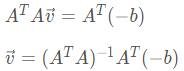
写成如下形式：

　　

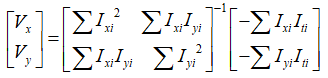
根据上式通过累加邻域像素点在三个维度的偏导数并做矩阵运算，即可算出该点的光流(Vx,Vy)。

源代码及效果：

源代码见这里：https://blog.csdn.net/xiaoyufei117122/article/details/53693627。

效果并不好，很多错误匹配点。

参考文献：

[1]. Lucas B and Kanade T. An Iterative Image RegistrationTechnique with an Application to Stereo Vision. Proc. Of 7th InternationalJoint Conference on Artificial Intelligence (IJCAI), pp.674-679.