disjoint set

MAKE-SET.x/ creates a new set whose only member (and thus representative)

is x. Since the sets are disjoint, we require that x not already be in some other

set.

UNION.x; y/ unites the dynamic sets that contain x and y, say Sx and Sy, into a

new set that is the union of these two sets. We assume that the two sets are disjoint

prior to the operation. The representative of the resulting set is any member

of Sx [ Sy, although many implementations of UNION specifically choose the

representative of either Sx or Sy as the new representative. Since we require

the sets in the collection to be disjoint, conceptually we destroy sets Sx and Sy,

removing them from the collection S. In practice, we often absorb the elements

of one of the sets into the other set.

FIND-SET.x/ returns a pointer to the representative of the (unique) set containing

x.

linklist implement

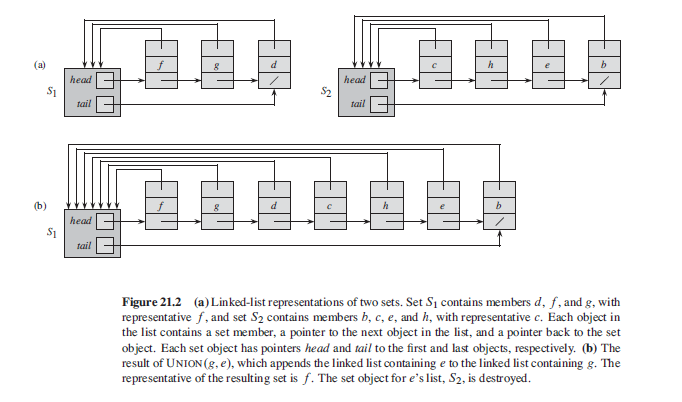
In the worst case, the above implementation of the UNION procedure requires an

average of ‚.n/ time per call because we may be appending a longer list onto

a shorter list; we must update the pointer to the set object for each member of

the longer list. Suppose instead that each list also includes the length of the list

(which we can easily maintain) and that we always append the shorter list onto the

longer, breaking ties arbitrarily. With this simple weighted-union heuristic, a single

UNION operation can still take _.n/ time if both sets have _.n/ members. As

the following theorem shows, however, a sequence of m MAKE-SET, UNION, and

FIND-SET operations, n of which are MAKE-SET operations, takes O.m C n lg n/

time.

Tree implement

Heuristics to improve the running time

So far, we have not improved on the linked-list implementation. A sequence of

n 1 UNION operations may create a tree that is just a linear chain of n nodes. By

using two heuristics, however, we can achieve a running time that is almost linear

in the total number of operations m.

The first heuristic, union by rank, is similar to the weighted-union heuristic we

used with the linked-list representation. The obvious approach would be to make

the root of the tree with fewer nodes point to the root of the tree with more nodes.

Rather than explicitly keeping track of the size of the subtree rooted at each node,

we shall use an approach that eases the analysis. For each node, we maintain a

rank, which is an upper bound on the height of the node. In union by rank, we

make the root with smaller rank point to the root with larger rank during a UNION

operation.

The second heuristic, path compression, is also quite simple and highly effective.

As shown in Figure 21.5, we use it during FIND-SET operations to make each

node on the find path point directly to the root. Path compression does not change

any ranks(more nodes linked to the root will cause much possibility to find it).

When we use both union by rank and path compression, the worst-case running
time is O.m ˛.n//, where ˛.n/ is a very slowly growing function, which we define
in Section 21.4. In any conceivable application of a disjoint-set data structure,
˛.n/ 4; thus, we can view the running time as linear in m in all practical situations.
Strictly speaking, however, it is superlinear. In Section 21.4, we prove this
upper bound.

 package disjoint_sets;
 // there have two ways,one is the linkedlist,the other is the tree,use the tree here
 public class disjoint_set {
     private static class Node{
         private Node p;
         private int rank;
         private String name;
         public Node(String na){
             p = this; rank = 0;name = na;
         }
     }
     public static void union(Node x,Node y){
         link(findset(x),findset(y));
     }
     public static void link(Node x,Node y){
         if(x.rank > y.rank){
             y.p = x;
         }
         else if(y.rank > x.rank){
             x.p = y;
         }
         else{
             y.p = x;
             x.rank = x.rank + 1;
         }
     }
     public static Node findset(Node x){
         if(x != x.p){
             x.p = findset(x.p);  //path compression
         }
         return x.p;
     }
     public static void print(Node x){

             System.out.println(x.name);
             if(x != x.p){
             x = x.p;
             print(x);
             }
             return;
     }
     public static void main(String[] args) {
         Node a = new Node("a");
         Node b = new Node("b");
         Node c = new Node("c");
         Node d = new Node("d");
         union(a,b);
         union(b,c);
         union(a,d);
         print(d);

     }

 }