拉格朗日乘子法&KKT条件

朗日乘子法(Lagrange Multiplier)和KKT(Karush-Kuhn-Tucker)条件是求解约束优化问题的重要方法，在有等式约束时使用拉格朗日乘子法，在有不等约束时使用KKT条件。前提是：只有当目标函数为凸函数时，使用这两种方法才保证求得的是最优解。

1. 拉格朗日乘子法：

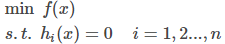
这个问题转换为

其中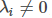，称为拉格朗日乘子。

　wikipedia上对拉格朗日乘子法的合理性解释：

　现有一个二维的优化问题：

　我们可以画图来辅助思考。

　　

　绿线标出的是约束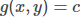的点的轨迹。蓝线是的等高线。箭头表示斜率，和等高线的法线平行。从图上可以直观地看到在最优解处，f和g的法线方向刚好相反（或者说叫梯度共线），即

　

　而满足（3）的点同时又是（4）的解。

　

　所以（2）和（4）等价。

　新方程F(x,y)在达到极值时与f(x,y)相等，因为F(x,y)达到极值时g(x,y)−c总等于零。

2.KKT条件

　

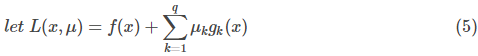
　其中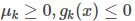

　

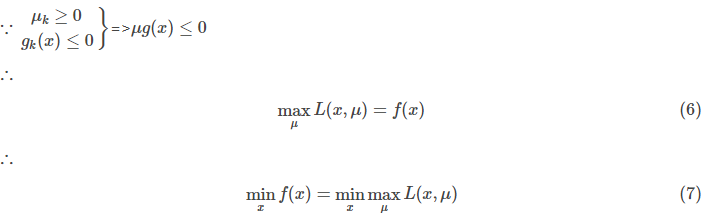
　上面的推导到此中断一下，我们看另外一个式子：

　

　这里的和都就向量，所以去掉了下标k。另外一些博友不明白上式中是怎么推出来的，其实很简单，因为f(x)与变量无关，所以这个等式就是成立的。

　又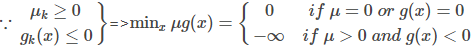

　

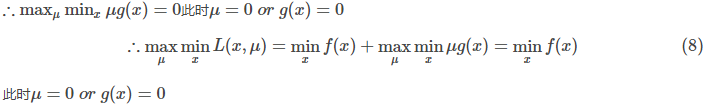
　联合(7)，(8)我们得到

　

　

增广朗日乘子法(Augumented Lagrange Multiplier)是对二次惩罚法（Quadratic Penalty Method）的一种改进，二次惩罚法要求二次惩罚项的系数趋近于无穷（对约束的偏离给予很高的惩罚）。

增广拉格朗日乘子法就是在原来的目标函数上加一个罚函数。罚函数因子的话就是拉格朗日乘子法，乘子就是罚函数法。因为有约束项，所以加上罚函数以后问题的解是不变的。然后就很自然的有了增广拉格朗日函数。求解的方法比如：从一个相对比较小的罚函数因子和选定的初始的乘子出发，在迭代中不断地求出，在把因子调大，同时更新乘子参数使其逼近最优的乘子。然后在罚函数因子变得非常大之前，一般就能把最优解得出来了。

多出一个二次惩罚项会使得算法的收敛速度很快，体现在理论上就是当很小时，每次乘子的更新可以变得很大。而且增广拉格朗日乘子法比拉格朗日乘子法普适性更好，需要的条件更加温和，比如不要求原函数是强凸的，甚至可以是非凸的，而且原函数可以趋近于无穷，而这种条件下，拉格朗日乘子法就无能为力了。究其原因，是因为二次惩罚项具有很好的矫正作用，在原函数非凸的情况下，只要满足一定的条件（二次惩罚项系数足够大），增广拉格朗日函数在最优点处的二阶导是正定的。因此具有严格的局部极小值。

来源：https://www.zhihu.com/question/23424344/answer/39935081

　　　https://www.zhihu.com/question/23424344/answer/79955670

　　　http://www.cnblogs.com/zhangchaoyang