【BZOJ】1040: [ZJOI2008]骑士（环套树dp）

http://www.lydsy.com/JudgeOnline/problem.php?id=1040

简直不能再神的题orz。

蒟蒻即使蒟蒻，完全不会。

一开始看到数据n<=1000000就傻了，简直O(n)的节奏。

翻了题解！做了2天！

蒟蒻的典范！

题解：

我们发现，每个人都有一条边，那么就有n条边，并且一定有一个环并且有且只有一个！

然后环套树的概念就是，一个环旁边插了很多树枝。。

就像这样：

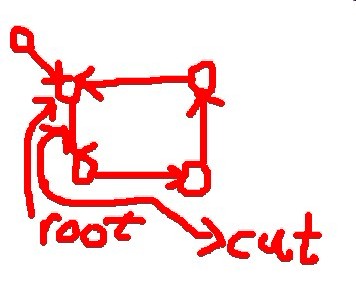
哈哈哈。。。

那么很好。。

如果这只是一颗树，那么太好做了，裸的树形dp，分选这个点和不选这个点更新，d[i][0]+=max(d[j][0], d[j][1]), (i, j); d[i][1]+=d[j][0],(i, j)

可是有环T_T

那么我们就切环！

怎么切合适呢。。。当然从度>1的点和他的孩子切开，然后自己做根（我们设这2个点为x和y）！（其实随便啦，，只要把环破掉就行了）

但是我们要注意。。树形dp的时候注意分情况，因为这2个点是联通的，当然就不能用d[i][1]（有x和有y的更新）和不能用d[i][2]（有x和有y的更新）。

也就是说吧，d[i][0]和d[i][1]是正常的树形dp，dp[i][2]和d[i][3]是环dp，只要在d[i][3]不更新y这个点就行了。否则就会造成x和y联通。

切的那条边是root的边，然后我们维护一个队列，里面放的是度为0的点（这点多想想。。//sad，，不就是拓扑序吗。。）

开代码什么的自己就理解了（表示抄lydrainbowcat的标程！）

#include <cstdio>
#include <cstring>
#include <cmath>
#include <string>
#include <iostream>
#include <algorithm>
using namespace std;
#define rep(i, n) for(int i=0; i<(n); ++i)
#define for1(i,a,n) for(int i=(a);i<=(n);++i)
#define for2(i,a,n) for(int i=(a);i<(n);++i)
#define for3(i,a,n) for(int i=(a);i>=(n);--i)
#define for4(i,a,n) for(int i=(a);i>(n);--i)
#define CC(i,a) memset(i,a,sizeof(i))
#define read(a) a=getint()
#define print(a) printf("%d", a)
#define dbg(x) cout << #x << " = " << x << endl
#define printarr(a, n, m) rep(aaa, n) { rep(bbb, m) cout << a[aaa][bbb]; cout << endl; }
inline const int getint() { int r=0, k=1; char c=getchar(); for(; c<'0'||c>'9'; c=getchar()) if(c=='-') k=-1; for(; c>='0'&&c<='9'; c=getchar()) r=r*10+c-'0'; return k*r; }
inline const int max(const int &a, const int &b) { return a>b?a:b; }
inline const int min(const int &a, const int &b) { return a<b?a:b; }

const int N=1000010;
int vis[N], q[N], front, tail, in[N], son[N], root[N], cnt, bak[N], n;
long long f[N][4], w[N], ans;
void dfs(const int &x) {
	vis[x]=x; int i;
	for(i=son[x]; !vis[i]; i=son[i]) vis[i]=x;
	if(vis[i]==x) {
		root[++cnt]=i; bak[son[i]]=1;
		--in[son[i]]; son[i]=0;
	}
}
void treedp() {
	int x, y;
	for1(i, 1, n) {
		f[i][1]=w[i];
		if(!bak[i]) f[i][3]=w[i];
	}
	for1(i, 1, n) if(!in[i]) q[tail++]=i;
	while(front!=tail) {
		x=q[front++]; if(front==N) front=0;
		y=son[x];
		if(!y) continue;
		f[y][0]+=max(f[x][1], f[x][0]);
		f[y][1]+=f[x][0];
		f[y][2]+=max(f[x][2], f[x][3]);
		if(!bak[y]) f[y][3]+=f[x][2];
		--in[y];
		if(!in[y]) { q[tail++]=y; if(tail==N) tail=0; }
	}
}

int main() {
	read(n);
	for1(i, 1, n) {
		read(w[i]); read(son[i]);
		++in[son[i]];
	}
	for1(i, 1, n) if(!vis[i]) dfs(i);
	treedp();
	for1(i, 1, cnt) ans+=max(f[root[i]][0], f[root[i]][3]);
	printf("%lld", ans);
	return 0;
}

---

Description

Z 国的骑士团是一个很有势力的组织，帮会中汇聚了来自各地的精英。他们劫富济贫，惩恶扬善，受到社会各界的赞扬。最近发生了一件可怕的事情，邪恶的Y国发动 了一场针对Z国的侵略战争。战火绵延五百里，在和平环境中安逸了数百年的Z国又怎能抵挡的住Y国的军队。于是人们把所有的希望都寄托在了骑士团的身上，就 像期待有一个真龙天子的降生，带领正义打败邪恶。骑士团是肯定具有打败邪恶势力的能力的，但是骑士们互相之间往往有一些矛盾。每个骑士都有且仅有一个自己 最厌恶的骑士（当然不是他自己），他是绝对不会与自己最厌恶的人一同出征的。战火绵延，人民生灵涂炭，组织起一个骑士军团加入战斗刻不容缓！国王交给了你 一个艰巨的任务，从所有的骑士中选出一个骑士军团，使得军团内没有矛盾的两人（不存在一个骑士与他最痛恨的人一同被选入骑士军团的情况），并且，使得这支 骑士军团最具有战斗力。为了描述战斗力，我们将骑士按照1至N编号，给每名骑士一个战斗力的估计，一个军团的战斗力为所有骑士的战斗力总和。

Input

第一行包含一个正整数N，描述骑士团的人数。接下来N行，每行两个正整数，按顺序描述每一名骑士的战斗力和他最痛恨的骑士。

Output

应包含一行，包含一个整数，表示你所选出的骑士军团的战斗力。

Sample Input

3
10 2
20 3
30 1

Sample Output

30
【数据规模】
对于30%的测试数据，满足N ≤ 10；
对于60%的测试数据，满足N ≤ 100；
对于80%的测试数据，满足N ≤ 10 000。
对于100%的测试数据，满足N ≤ 1 000 000，每名骑士的战斗力都是不大于 1 000 000的正整数。

HINT

Source