Machine Learning in Action -- 回归

机器学习问题分为分类和回归问题
回归问题，就是预测连续型数值，而不像分类问题，是预测离散的类别

至于这类问题为何称为回归regression，应该就是约定俗成，你也解释不通
比如为何logistic regression叫逻辑回归，明明解决的是分类问题，而且和逻辑没有半点关系

谈到回归，最简单的就是线性回归
用直线去拟合数据点，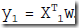

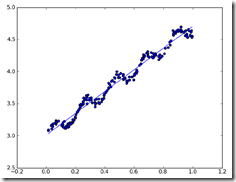
我们通常用平方误差来作为目标函数，称为最小二乘（ordinary least squares），参考AndrewNG的讲义

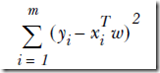
如何解这个问题，可以用梯度下降，但其实更简单的是，这个问题是有解析解的，可以直接求出

目标函数可以表示为，

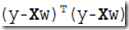
对w求导，得到

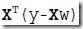
让导数=0，即可求出w

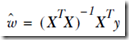
源码，

from numpy import *
def standRegres(xArr,yArr):
    xMat = mat(xArr); yMat = mat(yArr).T
    xTx = xMat.T*xMat
    if linalg.det(xTx) == 0.0: #判断行列式是否为0，为0是奇异矩阵，求不出逆
        print "This matrix is singular, cannot do inverse"
        return
    ws = xTx.I * (xMat.T*yMat)
    return ws

对于线性回归，是典型的高bias，低variance的模型，因为它可以说是最简单的模型

所以会出现欠拟合（underfit）的问题

 

Locally weighted linear regression

线性回归是最小均方差的无偏估计，局部加权也可以看成在估计中引入一些偏差，以降低预测的均方差

其实局部加权，是对训练集的一个选择（选择部分样本，所以产生偏差），选择离当前预测点比较近的那部分训练样本来进行线性回归，具体算法参考AndrewNG的讲义

如何选择，通过给每个训练样本加上一个权值w

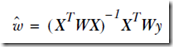
基本思路是，离预测点越近则权值越大，抽象表示就是高斯核

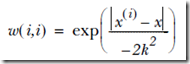
其中k代表，选取训练样本的范围

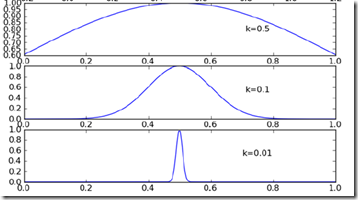
源码，

def lwlr(testPoint,xArr,yArr,k=1.0):
    xMat = mat(xArr); yMat = mat(yArr).T
    m = shape(xMat)[0]
    weights = mat(eye((m))) #weight初始化为单位矩阵
    for j in range(m):
        diffMat = testPoint - xMat[j,:] #预测x和每个样本的差值
        weights[j,j] = exp(diffMat*diffMat.T/(-2.0*k**2)) #计算每个样本的权值
    xTx = xMat.T * (weights * xMat)
    if linalg.det(xTx) == 0.0:
        print "This matrix is singular, cannot do inverse"
        return
    ws = xTx.I * (xMat.T * (weights * yMat))
    return testPoint * ws

和线性回归的差别就是多了权值的计算，注意这里权值矩阵是对角矩阵，对角线上表示每个样本的权值，其他都为0

当然局部加权可以解决欠拟合问题，拟合程度取决于k的取值

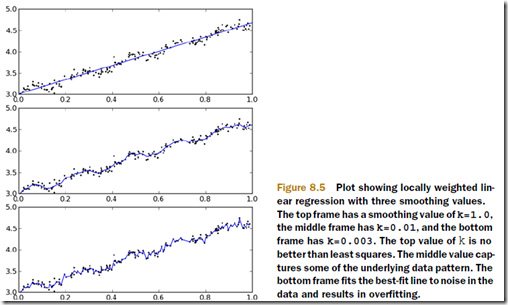
可见如果k选的过小，也会导致过拟合问题

当然这个算法的问题是，它是non-parametric algorithm，在预测的时候，需要保留完整的训练集，并每次预测都需要遍历整个训练集

 

Ridge regression

前面说的局部加权通过选择部分训练样本，来加入偏差，从而解决欠拟合的问题

下面要看看另外一类问题，

求解线性回归的时候，需要求解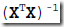

但有些时候，X协方差矩阵是求不出逆的，这个问题我们在因子分解里面也看到过

比如当样本数小于特征数时，或X非满秩，即某些样本是线性相关的，比如x1 = 2*x2

对于这种问题，直接求解会有问题，解决办法就是shringking特征，即选取部分特征，加入偏差

其中一种方法，叫做岭回归，

ridge regression中的目标函数为，加入了罚项

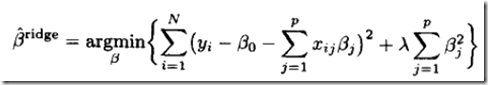
其中两部分，第一部分其实就是把线性回归中的y-xTw展开了，等价的

多的就是第二部分，可见如果要整个式子最小，那么如果单纯看第二部分，那么它为0是最优的

即所有参数都为0，这就是加入罚项，会趋于让某些不重要的特征的参数接近0，从而达到减少特征的目的

其中lamda是复杂度，lamda越大，shringking越厉害，即参数越趋向于0

也可以表示为，意思是一样的，限制参数

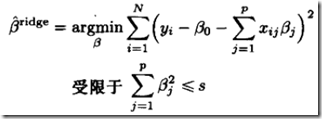
岭回归的解析解为，

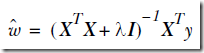
源码，

def ridgeRegres(xMat,yMat,lam=0.2):
    xTx = xMat.T*xMat
    denom = xTx + eye(shape(xMat)[1])*lam #加入罚项
    if linalg.det(denom) == 0.0:
        print "This matrix is singular, cannot do inverse"
        return
    ws = denom.I * (xMat.T*yMat)
    return ws

注意任意要做特征shrinking的算法，包括PCA，因子分析。。。首先都要对所有特征做normalization，否则无法评判各个特征

所以给出如何使用ridge regression的代码，看看如何做normalization

def ridgeTest(xArr,yArr):
    xMat = mat(xArr); yMat=mat(yArr).T
    yMean = mean(yMat,0)
    yMat = yMat - yMean
    xMeans = mean(xMat,0)
    xVar = var(xMat,0)
    xMat = (xMat - xMeans)/xVar #各个特征的scale不一样，所以要除以方差
    numTestPts = 30
    wMat = zeros((numTestPts,shape(xMat)[1]))
    for i in range(numTestPts):
        ws = ridgeRegres(xMat,yMat,exp(i-10))
        wMat[i,:]=ws.T
    return wMat

这里尝试30个不同的lamda，这里lamda以指数级别变化，可以看看极大和极小的lamda对结果的影响

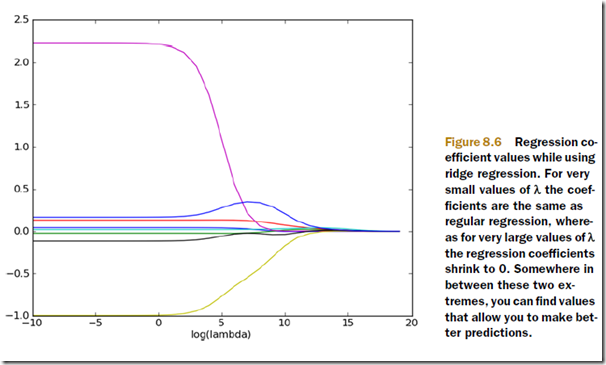
可以看到当lamda很小时，最左边，特征参数没有任何shrinking，和线性回归得到的值基本相同

而lamda很大时，最右边，特征参数会全部shrinking成0

所以要通过交叉验证来找到中间那个比较合适的lamda值

 

lasso

和ridge regression很像

只是从ridge regression的L2罚项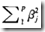 ，替换成L1罚项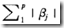

其中L1，和L2分别表示绝对值和平方，不要纠结

所以lasso可以表示为，

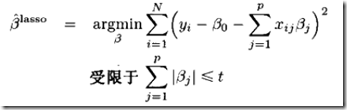
你可能会问，这个有毛区别，从平方变成绝对值？

答案是，lasso当t足够小的时候，更容易让某些特征参数直接=0，而不仅仅接近0，这样shrinking的效果更好

但是平方约束，是凸的，而换成绝对值，非凸约束，所以计算的时候会很麻烦（个人理解）

所以lasso很难求解

所以介绍一个近似方法

Forward stagewise regression

贪心算法，每次比较小的修正一个参数，然后如果可以减小误差，则保留，不停迭代找到最优的参数

def stageWise(xArr,yArr,eps=0.01,numIt=100):
    xMat = mat(xArr); yMat=mat(yArr).T
    yMean = mean(yMat,0)
    yMat = yMat - yMean
    xMat = regularize(xMat)
    m,n=shape(xMat)
    ws = zeros((n,1)); wsTest = ws.copy(); wsMax = ws.copy() #权值初始化为0
    for i in range(numIt):  #迭代次数
        print ws.T
        lowestError = inf;  #最小误差初始化为无穷
        for j in range(n):  #对于每个特征
            for sign in [-1,1]: #增加或减少权值
                wsTest = ws.copy()
                wsTest[j] += eps*sign #改变权值
                yTest = xMat*wsTest  #计算预测值
                rssE = rssError(yMat.A,yTest.A)  #计算预测平方误差，
                if rssE < lowestError:
                    lowestError = rssE
                    wsMax = wsTest
        ws = wsMax.copy()
        returnMat[i,:]=ws.T
    return returnMat

通过设置不同的eps值，即步长，来找到更合适的eps值

这个方法在足够次的迭代后，可以得到和lasso接近的结果

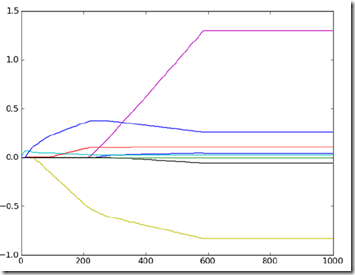
使用这个方法还有个很大的好处，是可以帮助理解当前的模型，可以简单的找到那些不重要的特征

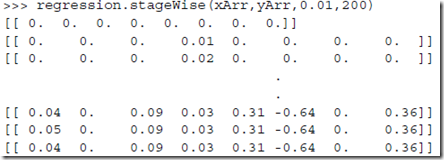
可以看到这迭代过程中，第二个和第七个特征的参数一直是0，说明这两个特征对误差没有贡献