Concat层解析

Concat层的作用就是将两个及以上的特征图按照在channel或num维度上进行拼接，并没有eltwise层的运算操作，举个例子，如果说是在channel维度上进行拼接conv_9和deconv_9的话，首先除了channel维度可以不一样，其余维度必须一致（也就是num、H、W一致），这时候所做的操作仅仅是conv_9 的channel k₁加上deconv_9的channel k₂，Concat 层输出的blob可表示为：N*（k₁+k₂）*H*W。通常情况下，考虑到Concat是希望将同大小的特征图拼接起来，那为什么会产生同大小的特征图呢？显然离不开上采样和下采样的操作，接下来，以Caffe为例，介绍一下这两种拼接的方式，如下：

• 选择axis=0，表示在num维度上进行拼接，可表示为：（k₁+k₂）*C*H*W；
• 选择axis=1，表示在channel维度上进行拼接，可表示为：N*（k₁+k₂）*H*W。

注意，卷积运算是三维的（不要想成二维的，当然这应该在学卷积的时候说过的），卷积核的数量就是feature map的channel，feature map的num通常是minibatch的数目。可问题是，这两种Concat的方式应该如何选择呢？（ps：如果自己不会用，很自然就是看看别人怎么用）

那么接下来我们就看看到底怎么用。

目前我见过的大都是在channel维度上进行拼接，其实也容易想到，因为我们说feature map 的num是minibatch的图片数目，比方我们的batch是32，但是我们有4张显卡同时训练，显然minibatch等于8，这个8表示的是每张显卡一次性处理的图片数目，这么说来，如果在num维度上拼接的意思就是将同一张显卡处理的feature map数目重复的加倍了，当然由于上下采样并不是严格的互逆运算，所以在重复的特征图上像素值还是存在差异。反之，如果是在channel 维度上拼接，此时channel 的数量增加了，也就是说同一个大小的特征图有了更多的特征表示，很多论文都已经证实其可以提高检测性能，但是如果不是cancat的方式，而是增加原有的卷积层的channel数目会导致显存占用增加，速度下降，这样一来concat的方式在不失速度的前提下，提高了精度，这也是其主要的贡献。当然光说不行，我把这两种方法都试验一下，供大家参考。

在试验之前介绍一下我的环境，我采用的是VGG模型加的改进，训练中用了4个TITAN X，minibatch等于8，在保证其它情况一致的情况下进行如下试验：

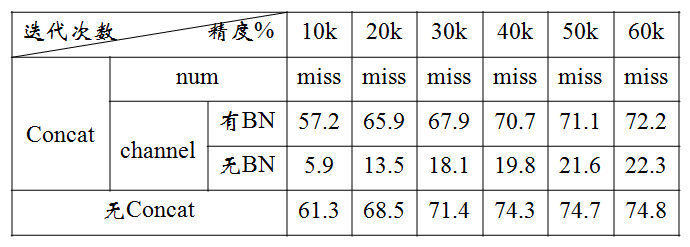
1. 在num维度上进行拼接；显然，在num维度上拼接的话，concat层输出的num个数就变成16了，如下表统计的结果显示，此种操作的效果很差，出现missing GT position for label的warning，不建议使用。
2. 在channel维度上进行拼接，在channel维度上的拼接分成无BN层和有BN层。

（1）无BN层：直接将deconvolution layer 和convolution layer concat。实验结果表明，该方式取得的结果精度较低，低于原有的VGG模型，分析主要的原因是漏检非常严重，原因应该是concat连接的两层参数不在同一个层级，类似BN层用在eltwise层上。

（2）有BN层：在deconvolution layer 和convolution layer 后面加batchnorm和scale层（BN）后再concat。实验结果表明，该方式取得了比原有VGG模型更好的检测效果（表中的迭代次数还没有完哦），增加了2%的精度，但是速度上慢了一些。

总结：concat层多用于利用不同尺度特征图的语义信息，将其以增加channel的方式实现较好的性能，但往往应该在BN之后再concat才会发挥它的作用，而在num维度的拼接较多使用在多任务问题上，将在后续的博客中介绍，总之concat层被广泛运用在工程研究中。