写在前面

对于刚学树剖的同学比如我这种大大大蒟蒻来说，做这题会给你带来很大的提升：不仅可以对树剖有更深刻的理解，还可以更好的理解线段树，所以这是一道好题哦

为了更好懂，我一点一点说说思路吧

思路

首先这题题意不难懂，只有两个操作：区间颜色修改和区间查询颜色数量，我们分开来看：

区间查询颜色个数

这是这题的难点，弄懂了以后可以对线段树有个蛮大的提升吧

我们先把问题简化一下，假设这不是一棵树，只是一条连（已经树剖过了），给定每个元素的颜色，问有几段颜色（就是这题中颜色数量的定义），我们怎么做呢？

首先我们可以知道，为了保障时间复杂度，这题肯定是用线段树求解的，最先想到的是叶子节点的颜色个数为1，因为此时不存在有颜色会重复，按线段树的做法，现在要回溯求更大区间的颜色个数了，我们怎样求解呢？

其实分情况讨论一下就可以知道了：见下

第一种情况：

左区间：1231（颜色个数为4） 右区间：222（个数为1）

合并后：1231222（颜色个数为4+1=5）

这是第一种情况：没有重复

我们再来看第二种：

左区间：1231（颜色个数为4）右区间：121（个数为3）

合并后：1231121（颜色个数为4+3-1）

这就是第二种情况了，左区间的最后一个颜色和右区间的第一个颜色重合，也就重复了，所以总数减一

综上所述：我们用数组lc[ ]和rc[ ]表示区间左右颜色，线段树维护区间颜色总数，就可以解决链情况下的此问题了

  1. int lc[maxn << 2];//这里要开4倍大小，因为是对应线段树节点的
  2. int rc[maxn << 2];
  3. void build(int id,int l,int r){
  4. 	tree[id].l = l;
  5. 	tree[id].r = r;
  6. 	if(l == r){
  7. 		tree[id].c = col[ori[l]];//赋值：叶子颜色
  8. 		lc[id] = rc[id] = col[ori[l]];//赋值：区间左颜色和区间右颜色
  9. 		tree[id].sum = 1;//颜色数为1
  10. 		return ;
  11. 		}
  12. 	int mid = l + r >> 1;
  13. 	build(lid,l,mid);
  14. 	build(rid,mid + 1,r);
  15. 	tree[id].sum = tree[lid].sum + tree[rid].sum;
  16. 	if(rc[lid] == lc[rid])tree[id].sum -= 1;
  17. 	lc[id] = lc[lid];
  18. 	rc[id] = rc[rid];
  19. 	}
  20. void pushdown(int id){
  21. 	if(tree[id].lazy != 0 && tree[id].l != tree[id].r){
  22. 		int c = tree[id].lazy;
  23. 		tree[lid].lazy = tree[rid].lazy = c;//粉刷
  24. 		tree[lid].c = tree[rid].c = c;
  25. 		lc[lid] = rc[lid] = lc[rid] = rc[rid] = c;//更新左右
  26. 		tree[lid].sum = tree[rid].sum = 1;//粉刷完以后只有一种颜色了
  27. 		tree[id].lazy = 0;
  28. 		}
  29. 	}
  30. int query(int id,int l,int r){
  31. 	pushdown(id);
  32. 	if(tree[id].l == l && tree[id].r == r){
  33. 		return tree[id].sum;
  34. 		}
  35. 	int mid = tree[id].l + tree[id].r >> 1;
  36. 	if(mid < l){
  37. 		return query(rid,l,r);
  38. 		}
  39. 	else if(mid >= r){
  40. 		return query(lid,l,r);
  41. 		}
  42. 	else{
  43. 		int ret = query(lid,l,mid) + query(rid,mid + 1,r);
  44. 		if(rc[lid] == lc[rid])ret -= 1;
  45. 		return ret;
  46. 		}
  47. 	}

值得注意的是：不要忘记大区间要继承小区间的左右端点颜色

树上查询颜色个数

我们的操作时基于树形的，所以树剖过后，我们树剖的查询函数要略作修改。

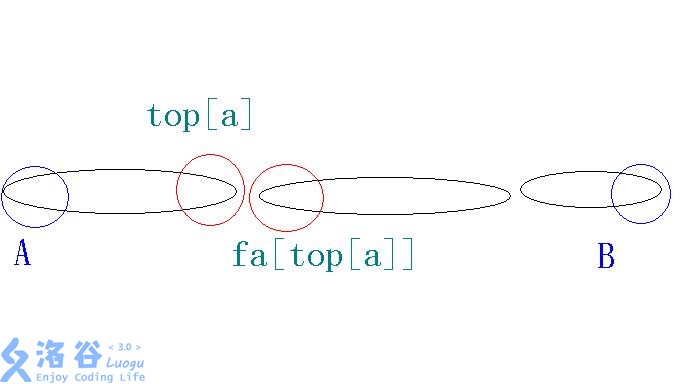
如上图：树剖就是把两点之间剖成了若干条链，我们还是要解决不同的链之间颜色重复问题。上图已经很明朗了：解决top[a]与fa[top[a]]颜色重复问题即可：

我写了个函数Qc来查询单点的颜色，其他学过树剖的应该不会太陌生：

  1. int query(int id,int l,int r){
  2. 	pushdown(id);
  3. 	if(tree[id].l == l && tree[id].r == r){
  4. 		return tree[id].sum;
  5. 		}
  6. 	int mid = tree[id].l + tree[id].r >> 1;
  7. 	if(mid < l){
  8. 		return query(rid,l,r);
  9. 		}
  10. 	else if(mid >= r){
  11. 		return query(lid,l,r);
  12. 		}
  13. 	else{
  14. 		int ret = query(lid,l,mid) + query(rid,mid + 1,r);
  15. 		if(rc[lid] == lc[rid])ret -= 1;
  16. 		return ret;
  17. 		}
  18. 	}
  19. int Qc(int id,int l,int r){
  20. 	pushdown(id);
  21. 	if(tree[id].l == l && tree[id].r == r){
  22. 		return tree[id].c;
  23. 		}
  24. 	int mid = tree[id].l + tree[id].r >> 1;
  25. 	if(mid < l)return Qc(rid,l,r);
  26. 	else return Qc(lid,l,r);
  27. 	}
  28. int Qsum(int x,int y){
  29. 	int ans = 0,Cson,Cfa;//儿子的颜色，爸爸的颜色
  30. 	while(top[x] != top[y]){
  31. 		if(dep[top[x]] < dep[top[y]])swap(x,y);
  32. 		ans += query(1,pos[top[x]],pos[x]);//累加答案
  33. 		Cson = Qc(1,pos[top[x]],pos[top[x]]);
  34. 		Cfa = Qc(1,pos[fa[top[x]]],pos[fa[top[x]]]);
  35. 		if(Cson == Cfa)ans -= 1;//重复则答案减一
  36. 		x = fa[top[x]];
  37. 		}
  38. 	if(dep[x] > dep[y])swap(x,y);
  39. 	ans += query(1,pos[x],pos[y]);
  40. 	return ans;
  41. 	}

区间修改

与普通的树剖题修改无大异，注意线段树中的颜色数量更新即区间端点继承即可

  1. void update(int id,int c,int l,int r){
  2. 	pushdown(id);
  3. 	if(tree[id].l == l && tree[id].r == r){
  4. 		tree[id].c = c;
  5. 		tree[id].lazy = c;
  6. 		tree[id].sum = 1;
  7. 		lc[id] = rc[id] = c;
  8. 		return ;
  9. 		}
  10. 	int mid = tree[id].l + tree[id].r >> 1;
  11. 	if(mid < l){
  12. 		update(rid,c,l,r);
  13. 		}
  14. 	else if(mid >= r){
  15. 		update(lid,c,l,r);
  16. 		}
  17. 	else{
  18. 		update(lid,c,l,mid);
  19. 		update(rid,c,mid + 1,r);
  20. 		}
  21. 	tree[id].sum = tree[lid].sum + tree[rid].sum;
  22. 	if(rc[lid] == lc[rid])tree[id].sum -= 1;
  23. 	lc[id] = lc[lid];
  24. 	rc[id] = rc[rid];
  25. 	}
  26. void uprange(int x,int y,int c){
  27. 	while(top[x] != top[y]){
  28. 		if(dep[top[x]] < dep[top[y]])swap(x,y);
  29. 		update(1,c,pos[top[x]],pos[x]);
  30. 		x = fa[top[x]];
  31. 		}
  32. 	if(dep[x] > dep[y])swap(x,y);
  33. 	update(1,c,pos[x],pos[y]);
  34. 	}

AC代码

就不多提啦，祝大家天天AC！

（重要注释已经打在上面思路部分了，这里直接给代码）

  1. #include<iostream>
  2. #include<cstdio>
  3. #include<queue>
  4. #include<cstring>
  5. #include<algorithm>
  6. using namespace std;
  7. int RD(){
  8.     int out = 0,flag = 1;char c = getchar();
  9.     while(c < '0' || c >'9'){if(c == '-')flag = -1;c = getchar();}
  10.     while(c >= '0' && c <= '9'){out = out * 10 + c - '0';c = getchar();}
  11.     return flag * out;
  12.     }
  13. const int maxn = 100019;
  14. int num,na,nume,cnt;
  15. int head[maxn];
  16. struct Node{int v,nxt;}E[maxn * 2];
  17. void add(int u,int v){
  18.     E[++nume].nxt = head[u];
  19.     E[nume].v = v;
  20.     head[u] = nume;
  21.     }
  22. int size[maxn],wson[maxn],dep[maxn],fa[maxn],top[maxn],pos[maxn],ori[maxn];
  23. int col[maxn];
  24. void dfs1(int id,int F){
  25.     size[id] = 1;
  26.     for(int i = head[id];i;i = E[i].nxt){
  27.         int v = E[i].v;
  28.         if(v == F)continue;
  29.         dep[v] = dep[id] + 1;
  30.         fa[v] = id;
  31.         dfs1(v,id);
  32.         size[id] += size[v];
  33.         if(size[v] > size[wson[id]])wson[id] = v;
  34.         }
  35.     }
  36. void dfs2(int id,int TP){
  37.     top[id] = TP;
  38.     pos[id] = ++cnt;
  39.     ori[cnt] = id;
  40.     if(!wson[id])return ;
  41.     dfs2(wson[id],TP);
  42.     for(int i = head[id];i;i = E[i].nxt){
  43.         int v = E[i].v;
  44.         if(v == fa[id] || v == wson[id])continue;
  45.         dfs2(v,v);
  46.         }
  47.     }
  48. int lc[maxn << 2];
  49. int rc[maxn << 2];
  50. #define lid (id << 1)
  51. #define rid (id << 1) | 1
  52. struct sag_tree{
  53. 	int l,r;
  54. 	int sum,c;//区间颜色总数，叶子颜色
  55. 	int lazy;//儿子的颜色
  56. 	}tree[maxn << 2];
  57. void build(int id,int l,int r){
  58. 	tree[id].l = l;
  59. 	tree[id].r = r;
  60. 	if(l == r){
  61. 		tree[id].c = col[ori[l]];//赋值：叶子颜色
  62. 		lc[id] = rc[id] = col[ori[l]];//赋值：区间左颜色和区间右颜色
  63. 		tree[id].sum = 1;//颜色数为1
  64. 		return ;
  65. 		}
  66. 	int mid = l + r >> 1;
  67. 	build(lid,l,mid);
  68. 	build(rid,mid + 1,r);
  69. 	tree[id].sum = tree[lid].sum + tree[rid].sum;
  70. 	if(rc[lid] == lc[rid])tree[id].sum -= 1;
  71. 	lc[id] = lc[lid];
  72. 	rc[id] = rc[rid];
  73. 	}
  74. void pushdown(int id){
  75. 	if(tree[id].lazy != 0 && tree[id].l != tree[id].r){
  76. 		int c = tree[id].lazy;
  77. 		tree[lid].lazy = tree[rid].lazy = c;//粉刷
  78. 		tree[lid].c = tree[rid].c = c;
  79. 		lc[lid] = rc[lid] = lc[rid] = rc[rid] = c;//更新左右
  80. 		tree[lid].sum = tree[rid].sum = 1;//粉刷完以后只有一种颜色了
  81. 		tree[id].lazy = 0;
  82. 		}
  83. 	}
  84. void update(int id,int c,int l,int r){
  85. 	pushdown(id);
  86. 	if(tree[id].l == l && tree[id].r == r){
  87. 		tree[id].c = c;
  88. 		tree[id].lazy = c;
  89. 		tree[id].sum = 1;
  90. 		lc[id] = rc[id] = c;
  91. 		return ;
  92. 		}
  93. 	int mid = tree[id].l + tree[id].r >> 1;
  94. 	if(mid < l){
  95. 		update(rid,c,l,r);
  96. 		}
  97. 	else if(mid >= r){
  98. 		update(lid,c,l,r);
  99. 		}
  100. 	else{
  101. 		update(lid,c,l,mid);
  102. 		update(rid,c,mid + 1,r);
  103. 		}
  104. 	tree[id].sum = tree[lid].sum + tree[rid].sum;
  105. 	if(rc[lid] == lc[rid])tree[id].sum -= 1;
  106. 	lc[id] = lc[lid];
  107. 	rc[id] = rc[rid];
  108. 	}
  109. int query(int id,int l,int r){
  110. 	pushdown(id);
  111. 	if(tree[id].l == l && tree[id].r == r){
  112. 		return tree[id].sum;
  113. 		}
  114. 	int mid = tree[id].l + tree[id].r >> 1;
  115. 	if(mid < l){
  116. 		return query(rid,l,r);
  117. 		}
  118. 	else if(mid >= r){
  119. 		return query(lid,l,r);
  120. 		}
  121. 	else{
  122. 		int ret = query(lid,l,mid) + query(rid,mid + 1,r);
  123. 		if(rc[lid] == lc[rid])ret -= 1;
  124. 		return ret;
  125. 		}
  126. 	}
  127. int Qc(int id,int l,int r){
  128. 	pushdown(id);
  129. 	if(tree[id].l == l && tree[id].r == r){
  130. 		return tree[id].c;
  131. 		}
  132. 	int mid = tree[id].l + tree[id].r >> 1;
  133. 	if(mid < l)return Qc(rid,l,r);
  134. 	else return Qc(lid,l,r);
  135. 	}
  136. void uprange(int x,int y,int c){
  137. 	while(top[x] != top[y]){
  138. 		if(dep[top[x]] < dep[top[y]])swap(x,y);
  139. 		update(1,c,pos[top[x]],pos[x]);
  140. 		x = fa[top[x]];
  141. 		}
  142. 	if(dep[x] > dep[y])swap(x,y);
  143. 	update(1,c,pos[x],pos[y]);
  144. 	}
  145. int Qsum(int x,int y){
  146. 	int ans = 0,Cson,Cfa;
  147. 	while(top[x] != top[y]){
  148. 		if(dep[top[x]] < dep[top[y]])swap(x,y);
  149. 		ans += query(1,pos[top[x]],pos[x]);
  150. 		Cson = Qc(1,pos[top[x]],pos[top[x]]);
  151. 		Cfa = Qc(1,pos[fa[top[x]]],pos[fa[top[x]]]);
  152. 		if(Cson == Cfa)ans -= 1;
  153. 		x = fa[top[x]];
  154. 		}
  155. 	if(dep[x] > dep[y])swap(x,y);
  156. 	ans += query(1,pos[x],pos[y]);
  157. 	return ans;
  158. 	}
  159. int main(){
  160. 	num = RD();na = RD();
  161. 	for(int i = 1;i <= num;i++)col[i] = RD();
  162. 	int u,v;
  163. 	for(int i = 1;i <= num - 1;i++){
  164. 		u = RD();v = RD();
  165. 		add(u,v);
  166. 		add(v,u);
  167. 		}
  168. 	dfs1(1,-1);
  169. 	dfs2(1,1);
  170. 	build(1,1,num);
  171. 	char ask;
  172. 	int c;
  173. 	for(int i = 1;i <= na;i++){
  174. 		cin>>ask;
  175. 		if(ask == 'Q'){
  176. 			u = RD();v = RD();
  177. 			printf("%d\n",Qsum(u,v));
  178. 			}
  179. 		else{
  180. 			u = RD();v = RD();c = RD();
  181. 			uprange(u,v,c);
  182. 			}
  183. 		}
  184. 	return 0;
  185. 	}

最后，虽然dalao没帮啥忙，可是我是看大佬以前的代码查出错的，宣传一下大佬

最后当然是大家最喜欢的广告啦

题解 P2486 【[SDOI2011]染色】的更多相关文章

  1. luogu题解P2486[SDOI2011]染色--树链剖分+trick

    题目链接 https://www.luogu.org/problemnew/show/P2486 分析 看上去又是一道强行把序列上问题搬运到树上的裸题,然而分析之后发现并不然... 首先我们考虑如何在 ...

  2. P2486 [SDOI2011]染色

    P2486 [SDOI2011]染色 树链剖分 用区间修改线段树维护 对于颜色段的计算:sum[o]=sum[lc]+sum[rc] 因为可能重复计算,即左子树的右端点和右子树的左端点可能颜色相同 多 ...

  3. Luogu P2486 [SDOI2011]染色(树链剖分+线段树合并)

    Luogu P2486 [SDOI2011]染色 题面 题目描述 输入输出格式 输入格式: 输出格式: 对于每个询问操作,输出一行答案. 输入输出样例 输入样例: 6 5 2 2 1 2 1 1 1 ...

  4. 洛谷 P2486 [SDOI2011]染色 树链剖分

    目录 题面 题目链接 题目描述 输入输出格式 输入格式 输出格式 输入输出样例 输入样例: 输出样例: 说明 思路 PushDown与Update Q AC代码 总结与拓展 题面 题目链接 P2486 ...

  5. 洛谷 P2486 [SDOI2011]染色/bzoj 2243: [SDOI2011]染色 解题报告

    [SDOI2011]染色 题目描述 给定一棵有n个节点的无根树和m个操作,操作有2类: 1.将节点a到节点b路径上所有点都染成颜色c: 2.询问节点a到节点b路径上的颜色段数量(连续相同颜色被认为是同 ...

  6. 洛谷P2486 [SDOI2011]染色 题解 树链剖分+线段树

    题目链接:https://www.luogu.org/problem/P2486 首先这是一道树链剖分+线段树的题. 线段树部分和 codedecision P1112 区间连续段 一模一样,所以我们 ...

  7. luogu P2486 [SDOI2011]染色

    树剖做法: 就是两个dfs+一个线段树 难度的取决基本==线段树的维护难度 所以对有点线段树基础的,树剖也不难做吧 这里操作有二 一:两点间路径染色 线段树的区间赋值操作 二:查询路径段的个数 考虑线 ...

  8. P2486 [SDOI2011]染色（树剖）区间覆盖+区间的连续段

    https://www.luogu.org/problemnew/show/P2486 值的一看https://www.cnblogs.com/Tony-Double-Sky/p/9283262.ht ...

  9. 洛谷 P2486 [SDOI2011]染色（树链剖分+线段树）

    题目链接 题解 比较裸的树链剖分 好像树链剖分的题都很裸 线段树中维护一个区间最左和最右的颜色,和答案 合并判断一下中间一段就可以了 比较考验代码能力 Code #include<bits/st ...

  10. 洛谷 P2486 [SDOI2011]染色

    题目描述 输入输出格式 输入格式: 输出格式: 对于每个询问操作,输出一行答案. 输入输出样例 输入样例#1: 6 5 2 2 1 2 1 1 1 2 1 3 2 4 2 5 2 6 Q 3 5 C ...

随机推荐

  1. [BUAA软工]第0次个人作业

    [BUAA软工]第0次个人作业 本次作业所属课程 : 2019BUAA软件工程 本次作业要求: 第0次个人作业 我在本课程的目标: 熟悉软件工程流程,规范开发习惯 本次作业的帮助: 熟悉课程流程 Pa ...

  2. 文件名命工具类（将指定目录下的文件的type类型的文件，进行重命名，命名后的文件将去掉type）

    import java.io.File; /** * <b>function:</b> 文件命名工具类 * @author hoojo * @createDate 2012-5 ...

  3. The user survey（用户调查）

    在周末,我们找了一些人来进行了一个调查,鉴于选择困难,我们只找到了几个真正的小学生,没有找到家长,其余那些都是找大学生来做调查的,我们和他们说,让他们把自己的立场看成是小学生或家长.下面是我们整理出来 ...

  4. golang 反射

    参考:|--http://blog.51cto.com/speakingbaicai/1707637 |--https://studygolang.com/articles/6324 反射是在gola ...

  5. 处理Git不能上传大于100M文件问题

    记录一下自己工作遇到的问题,免得下次再遇到了还到处网上查资料解决. 自己的项目的版本控制用的是Git,代码仓库在github托管.项目里用到了百度导航SDK,由于百度导航SDK有了新版本,于是就更新到 ...

  6. 微信之父张小龙经典演讲164页PPT:《微信背后的产品观》

    收藏地址:http://www.haokoo.com/internet/8974068.html

  7. 个人作业-week2（代码复审）

    一.代码复审check list 概要部分 代码符合需求和规格说明吗? 符合要求和规格说明,-s指令和-c指令都能实现需求.并且能够处理非法输入. 代码设计是否有周全的考虑? 程序的main函数中对各 ...

  8. express和数据库(MySQL)的交互(二)

    一.安装express前面都讲了 1.express. cnpm || npm install express --save 2.中间件 a.cnpm || npm install body-pars ...

  9. UVAlive4287_Proving Equivalences

    题意是告诉你有n个命题,m条递推关系,表示某个命题可以推出另外一个命题. 现在问你至少在增加多少个递推关系可以保证所有命题两两互推. 命题为点,关系为有向边,题目转化成为至少增加多少条有向边使得整个图 ...

  10. python自动化之读写

    ############################################################################# #############在Windows上 ...