poj1095

题意：给出n，要求输出第n个二叉树，二叉树编号规则如下图所示：

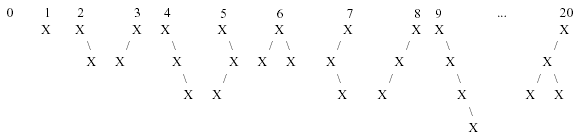
分析：g[i]表示有i个节点的二叉树，有多少种。f[i][j]表示有i个节点，且左子树有j个节点的树有多少种。

sumg[i]表示g数组前i个的和。sumf[i][j]表示f[i]数组前j项的和。

有g[i]=sum(f[i][j])，f[i][j]=g[j]*g[i - 1 - j]。

对于一个输入的n，我们先通过对sumg进行二分查找以确定节点数量，然后递归求解。

递归包含两个参数：1、当前子树节点数量tot。2、要求第num个具有这些节点的子树。

接下来在sumf[tot]中对num进行二分查找，即可确定其左子树节点个数x，从而确定其右子树的节点个数y。

通过g[y]（右子树的变化数）可以判定左子树处于第几个形态。计算公式为(num - sumf[tot][x - 1]) / g[y];

同样可以确定右子树处于哪一种形态。计算公式为(num - sumf[tot][x - 1]) % g[y];

#include <iostream>
using namespace std;

const    long long    maxx = ;

long long        f[maxx][maxx], g[maxx], sumg[maxx], sumf[maxx][maxx], n;

long long binarysearch(long long *array, long long start, long long end, long long goal)
{
    long long        l, r, mid;

    l = start;
    r = end;
    while (l < r)
    {
        mid = (l + r) / ;
        if (array[mid] < goal)
            l = mid + ;
        else
            r = mid;
    }
    return l;
}

void dfs(long long tot, long long num)
{
    long long        x = binarysearch(sumf[tot], , tot - , num), a, b;

    if (x > )
    {
        a = (num - sumf[tot][x - ]) / g[tot - x - ];
        b = (num - sumf[tot][x - ]) % g[tot - x - ];
        if (b == )
            b = g[tot - x - ];
        else
            a++;
        printf("(");
        dfs(x, a);
        printf(")");
        num = b;
    }
    printf("X");
    if (tot -  - x > )
    {
        printf("(");
        dfs(tot - x - , num);
        printf(")");
    }
}

void work()
{
    long long        num;

    num = binarysearch(sumg, , maxx, n);
    n -= sumg[num - ];
    dfs(num, n);
    printf("\n");
}

int main()
{
    long long        i, j;

    //freopen("t.txt", "r", stdin);
    f[][] = ;
    g[] = ;
    sumg[] = ;
    g[] = sumg[] = ;
    for (i = ; i < maxx; i++)
    {
        g[i] = sumf[i][] = f[i][] = g[i - ];
        for (j = ; j < i; j++)
        {
            f[i][j] = g[j] * g[i -  - j];
            g[i] += f[i][j];
            sumf[i][j] = sumf[i][j - ] + f[i][j];
        }
        sumg[i] = g[i] + sumg[i - ];
    }
    while (scanf("%d", &n) != EOF && n != )
        work();
    return ;
}