Manacher算法学习笔记

前言

Manacher（也叫马拉车）是一种用于在线性时间内找出字符串中最长回文子串的算法

算法

一般的查找回文串的算法是枚举中心，然后往两侧拓展，看最多拓展出多远。最坏情况下$O(n^2)$

然而Manacher能够充分利用回文的性质

首先，回文分为奇回文（比如$aba$）和偶回文（比如$abba$），如果分开来讨论会很麻烦。

于是我们在原串的首尾以及每两个字符之间各插入一个原串中没有出现过的字符。比如$abbbac$，变成$\%a\%b\%b\%b\%a\%c\%$

那么这样的话，上面的$aba$变成$\%a\%b\%a\%$，$abba$变成$\%a\%b\%b\%a\%$，都变成了奇回文

我们定义$p[i]$为以$i$为中心的回文串的最长半径，比如串$\%a\%b\%a\%$，其中$b$为第四个字符，则$p[4]=4$（因为以他为中心的最长回文串是$\%a\%b\%a\%$，而这个回文串的半径为4）

那么我们原串中以这个位置为中心的最长回文串长度就是$p[i]-1$（一个要去掉$\%$，然后半径的话要防止中心被多算一次）

那么现在的问题就是怎么快速求出$p[i]$了

我们假设$pos$是一个已经记录的值，$R$为以$pos$为中心的回文串的最长右边界，然后现在要求$p[i]$

$j$是$i$关于$pos$的对称点，也就是说$j=2*pos-i$

那么这个时候分为两种情况

1.$j$的最长回文没有跳出$L$

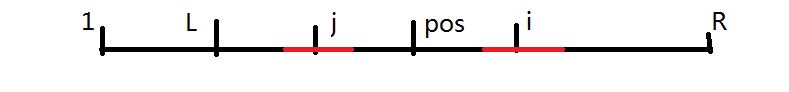
因为$[L...R]$是一个回文串，所以$i$的回文和$j$的回文相同，即$p[i]=p[j]$

2.$j$的最长回文越过了$L$

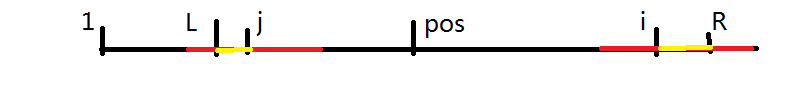
如果在这种情况下，$j$的最长回文就不一定是$i$的最长回文了。然后黄色那块肯定还是满足条件的

所以综上，$p[i]=min(p[2*pos-1],R-i)$

然后剩下的那部分怎么办？暴力直接算

我没口胡，真的

时间复杂度

时间复杂度是$O(n)$的

为啥嘞？

如果$p[i]$能直接求肯定是$O(1)$的

然后如果需要上暴力那么每一次都能让$R$严格右移

因为串长只有$O(n)$，所以暴力次数最多$O(n)$

上板子吧，板子抄的zzk大爷的

洛谷P3805 【模板】manacher算法

 // luogu-judger-enable-o2
 //minamoto
 #include<iostream>
 #include<cstdio>
 #include<cstring>
 using namespace std;
 #define getc() (p1==p2&&(p2=(p1=buf)+fread(buf,1,1<<21,stdin),p1==p2)?EOF:*p1++)
 char buf[<<],*p1=buf,*p2=buf;
 template<class T>inline bool cmax(T&a,const T&b){return a<b?a=b,:;}
 const int N=1.1e7+;
 int p[*N];char s[N],now[N*];
 inline bool is(char c){return c!='\n'&&c!=EOF;}
 inline void read(char *s){
     int len=;char ch;while(is(ch=getc())) s[++len]=ch;s[++len]=;
 }
 int manacher(char *s){
     int len=strlen(s+);
     for(int i=;i<=len;++i) now[*i-]='%',now[*i]=s[i];
     now[len=len*+]='%';
     int pos=,R=;
     for(int i=;i<=len;++i){
         if(i<R) p[i]=min(p[*pos-i],R-i);else p[i]=;
         while(i-p[i]>=&&i+p[i]<=len&&now[i-p[i]]==now[i+p[i]]) ++p[i];
         if(i+p[i]>R) pos=i,R=i+p[i];
     }
     int mx=;
     for(int i=;i<=len;++i) cmax(mx,p[i]-);
     return mx;
 }
 int main(){
 //    freopen("testdata.in","r",stdin);
     read(s);
     printf("%d\n",manacher(s));
     return ;
 }

不过我有个地方还没弄明白，就是上面求$p[i]$的时候，我写成这样也能A

     for(int i=;i<=len;++i){
         if(i<R) p[i]=min(p[*pos-i],R-i);else p[i]=;
         while(i-p[i]>=&&i+p[i]<=len&&now[i-p[i]]==now[i+p[i]]) ++p[i];
         if(i+p[i]->R) pos=i,R=i+p[i]-;
     }

话说如果我写成 p[i]=min(p[*pos-i],R-i+1) 我还能理解为是开区间和闭区间的不同……话说一个闭区间一个开区间为啥没问题啊……

先坑着，等会了再来填坑

洛谷P4555 [国家集训队]最长双回文串

首先双回文串肯定是拼接而成的

那么我们就记录一下每一个字符分别作为回文串的最左端（最右端）时，对应的中心最左（最右）在哪里

然后就可以通过拼接得到双回文串了

 //minamoto
 #include<iostream>
 #include<cstdio>
 #include<cstring>
 using namespace std;
 template<class T>inline bool cmax(T&a,const T&b){return a<b?a=b,:;}
 const int N=1e5+;
 int p[*N];char s[N],now[N*];int L[N<<],R[N<<],len,ans;
 void manacher(char *s){
     len=strlen(s+);
     for(int i=;i<=len;++i) now[*i-]='%',now[*i]=s[i];
     now[len=len*+]='%';
     int pos=,R=;
     for(int i=;i<=len;++i){
         if(i<R) p[i]=min(p[*pos-i],R-i);else p[i]=;
         while(i-p[i]>=&&i+p[i]<=len&&now[i-p[i]]==now[i+p[i]]) ++p[i];
         if(i+p[i]>R) pos=i,R=i+p[i];
     }
 }
 int main(){
 //    freopen("testdata.in","r",stdin);
     scanf("%s",s+);
     manacher(s);
     for(int i=,pos=;i<=len;++i)
     for(;pos<=i+p[i]-;++pos) L[pos]=i;
     for(int i=len,pos=len;i;--i)
     for(;pos>=i-p[i]+;--pos) R[pos]=i;
     for(int i=;i<=len;++i) cmax(ans,R[i]-L[i]);
     printf("%d\n",ans);
     return ;
 }

洛谷P1659 [国家集训队]拉拉队排练

因为题目要求的是奇数回文，所以连$\%$都没必要加了，直接上manacher就好了

然后因为一个半径为$n$的回文串存在，那么$n-1$,$n-2$的回文串也必定存在

所以要开一个桶存一下前缀和

然后还要用一下快速幂

然后就差不多了

 //minamoto
 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #define ll long long
 using namespace std;
 const int N=1e6+,mod=;
 char s[N];int p[N],c[N],n;ll ans=,sum=,k;
 inline ll qpow(ll a,ll b){
     ll res=;
     while(b){
         if(b&) (res*=a)%=mod;
         (a*=a)%=mod,b>>=;
     }
     return res;
 }
 int main(){
 //    freopen("testdata.in","r",stdin);
     scanf("%d%lld",&n,&k);
     scanf("%s",s+);
     for(int i=,pos=,R=;i<=n;++i){
         p[i]=i<R?min(p[*pos-i],R-i):;
         while(i-p[i]>=&&i+p[i]<=n&&s[i-p[i]]==s[i+p[i]]) ++p[i];
         if(i+p[i]->R) pos=i,R=i+p[i]-;
         ++c[*p[i]-];
     }
     (n&)?:(--n);
     for(int i=n;i;i-=){
         sum+=c[i];
         if(sum>k){(ans*=qpow(i,k))%=mod;break;}
         (ans*=qpow(i,sum))%=mod,k-=sum;
     }
     printf("%lld\n",sum<k?-:ans);
     return ;
 }