主成分分析法详解（PCA）

引用：https://blog.csdn.net/program_developer/article/details/80632779

将n维特征映射到k维上，只保留包含绝大部分方差的维度特征，而忽略包含方差几乎为0的特征维度，实现对数据特征的降维处理。

PCA算法有两种实现方法：基于特征值分解协方差矩阵实现PCA算法、基于SVD分解协方差矩阵实现PCA算法。

针对第一种方案基于特征值分解协方差，步骤为：

1：对原始矩阵X进行去平均值。

2：求原始矩阵的协方差。

3：根据协方差矩阵计算特征值和对应的特征向量和标准化特征向量。

4：根据特征值，将对应的标准化特征向量进行排序，每个特征向量写作行向量P

5：最终降维结果：Y=Pk*X

如计算：

1首先去平均值，每一位特征减去各自的平均值。平均值为0，减0仍为原值。

2之后计算协方差，。。得协方差矩阵。

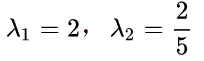3然后根据0，求得（5/6-λ)^2=16/25。求得λ：。根据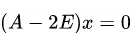，得当λ=2，X1=X2。令X1=1，则X2=1，特征向量P1=[1;1]，同理，P2=[1;-1].然后求出P1和P2的标准特征向量。组成P。

4根据特征值，进行排序并写作行向量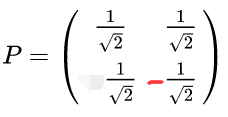：，降到1维，则取第一行

5最终降维

针对第二种方案基于SVD分解协方差：

1：对原始矩阵X进行去平均值。

2：根据SVD计算特征值和对应的特征向量和标准化特征向量。

3：根据特征值，将对应的标准化特征向量进行排序，每个特征向量写作行向量P

4：最终降维结果：Y=Pk*X

选择左奇异矩阵，进行使用，然后求得协方差矩阵的特征值与特征向量。

引用：https://link.zhihu.com/?target=https%3A//mp.weixin.qq.com/s/Dv51K8JETakIKe5dPBAPVg

SVD分解的算法过程为：

针对任意矩阵A，分解为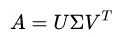：。U为A的行为参照的方阵，为左奇异矩阵。Σ和A的行列相同，除了对角线其它元素都为0。V为A的列为参照的方阵，为右奇异矩阵。

分解的步骤为：

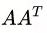1求出：，设为M，作为U的计算准备。，设为N作为V的计算准备。

2针对M矩阵求出特征值，特征向量。针对N矩阵求出特征值，特征向量。并将所求特征向量标准化为ui和vi。

3利用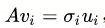根据ui和vi求出σ的所有值。

4将所有值进行归并，求出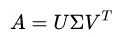表达式。并利用U获得原始A的特征值，特征向量。

例如：计算。

使用MATLAB的算法：

clear all,clc;
A=[[-1,1];[-2,-1];[-3,-2];[1,1];[2,1];[3,2]];
A_mean=A-mean(A);#去平均值
A_div=A_mean;
M=A_div'*A_div;
N=A_div*A_div';
[M_vector,M_val]=eig(M);
[N_vector,N_val]=eig(N);

M_vector=fliplr(M_vector);
N_vector=fliplr(N_vector);
%M_vector=flipud(M_vector)
%N_vector=flipud(N_vector)

M_val=diag(M_val);
N_val=diag(N_val);
M_val=flipud(M_val)
N_val=flipud(N_val)

theta1=sqrt(M_val(1));
theta2=sqrt(M_val(2));
cgma=zeros(size(A));
cgma(1,1)=theta1;
cgma(2,2)=theta2;
%-(N_vector*cgma*M_vector')
-N_vector*cgma

　　取第一列即获得了降维哦！