1897. tank 坦克游戏

传送门

显然考虑 $dp$，发现时间只和当前位置和攻击次数有关，设 $F[i][j][k]$ 表示当前位置为 $i,j$ ，攻击了 $k$ 次得到的最大分数

初始 $f[1][1][k]$ 为位置 $1,1$ 能打到的前 $k$ 大位置的分数和

每次移动都会多一行或多一列目标可以选择，攻击时显然优先攻击分数大的位置，因为要排序，

加上原本 $i,j,k$ 复杂度 $O(nm(T+ \log R)R)$ ，考虑优化

先考虑从 $f[i][j-1][k-t]$ 转移到 $f[i][j][k]$，设此时多打的 $t$ 个物品总价值为 $tmp[t]$

那么有 $f[i][j][k]=max(f[i][j-1][k-t]+tmp[t])$，然后我们能（并不）发现转移有单调性，即如果 $i,j,k$ 的最优决策点是 $t$

那么 $i,j,k+1$ 的最优决策点一定不小于 $t$，证明如下：

为了方便理解，我们把 $f[i][j-1][k-t]$ 时选择的数列看成一段区间，把 $tmp$ 看成另一段区间：

假设转移不单调，那么就会出现 $f[i][j][k+1]$ 的最优决策点 $t'<t$，在图上就是这个样子：

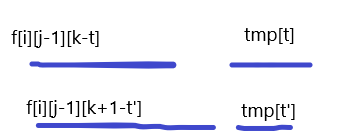
上面的是 $f[i][j][k]$ 的最优转移，下面的是 $f[i][j][k+1]$ 的最优转移

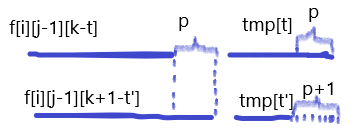
因为是最优，那么上面说明，左边的 $p$ 那一段没有右边的 $p$ 那一段的值大（不然就不是最优转移了）

但是下面的却有告诉我们，左边的 $p$ 那一段比右边的 $p+1$ 那一段的值大

然后就矛盾了，所以转移一定的单调的

然后就可以决策单调性分治把复杂度变成 $O(nm(T+R \log R))$

具体看代码

#include<iostream>
#include<cstdio>
#include<algorithm>
#include<cstring>
#include<cmath>
using namespace std;
typedef long long ll;
inline int read()
{
    int x=,f=; char ch=getchar();
    while(ch<''||ch>'') { if(ch=='-') f=-; ch=getchar(); }
    while(ch>=''&&ch<='') { x=(x<<)+(x<<)+(ch^); ch=getchar(); }
    return x*f;
}
const int N=,M=;
inline bool cmp(const int &x,const int &y) { return x>y; }//从大到小排序
int n,m,S,T,a[N][N],f[N][N][M],ans;
int g[M],v[M],tmp[N*N],tot;
void solve(int ql,int qr,int l,int r)
{
    if(ql>qr) return; int mid=ql+qr>>,pos=l;//pos记录决策点
    for(int i=l;i<=r&&i<=mid;i++)
    {
        int t=g[mid-i]+tmp[i];
        if(t>v[mid]) v[mid]=t,pos=i;
    }
    solve(ql,mid-,l,pos); solve(mid+,qr,pos,r);
}
int main()
{
    memset(f,~0x3f,sizeof(f));//一开始都不合法
    n=read(),m=read(),S=read(),T=read();
    for(int i=;i<=n;i++)
        for(int j=;j<=m;j++) a[i][j]=read();
    for(int i=;i<=S+;i++)
        for(int j=;j<=S+;j++) if(a[i][j]>) tmp[++tot]=a[i][j];
    sort(tmp+,tmp+tot+,cmp); tot=min(tot,T);
    f[][][]=; for(int k=;k<=tot;k++) f[][][k]=f[][][k-]+tmp[k];//初始化
    int nn=max(,n-S),mm=max(,m-S);
    for(int i=;i<=nn;i++)
        for(int j=;j<=mm;j++)
        {
            int mx=T-i-j+; if(mx<=) continue;//mx是剩下的时间
            if(i>)
            {
                for(int k=;k<=mx;k++) g[k]=v[k]=f[i-][j][k];
                if(i+S<=n)
                {
                    tot=;
                    for(int k=max(,j-S);k<=min(j+S,m);k++) if(a[i+S][k]>) tmp[++tot]=a[i+S][k];
                    sort(tmp+,tmp+tot+,cmp); for(int k=;k<=tot;k++) tmp[k]+=tmp[k-];
                    if(tot) solve(,mx,,tot);
                }
                for(int k=;k<=mx;k++) f[i][j][k]=v[k];
            }
            if(j>)
            {
                for(int k=;k<=mx;k++) g[k]=v[k]=f[i][j-][k];
                if(j+S<=m)
                {
                    tot=;
                    for(int k=max(,i-S);k<=min(i+S,n);k++) if(a[k][j+S]>) tmp[++tot]=a[k][j+S];
                    sort(tmp+,tmp+tot+,cmp); for(int k=;k<=tot;k++) tmp[k]+=tmp[k-];
                    if(tot) solve(,mx,,tot);
                }
                for(int k=;k<=mx;k++) f[i][j][k]=max(f[i][j][k],v[k]);
            }
            for(int k=;k<=mx;k++) ans=max(ans,f[i][j][k]);
        }
    printf("%d\n",ans);
    return ;
}