洛谷 P2024 [NOI2001]食物链（种类并查集，加权并查集）

传送门

---

解题思路

加权并查集：

什么是加权并查集？

就是记录着每个节点到它的父亲的信息（权值等）。

难点：在路径压缩和合并节点时把本节点到父亲的权值转化为到根节点的权值

怎么转化呢？

每道题都不一样QAQ

看一看这道题我们用r[x]=0表示是x和f[x]是同种生物，等于1表示x吃f[x]，等于2表示x是f[x]的食物。

从x点到f[x]的权值更新为i点到祖宗的权值的方法：

由于路径压缩是递归实现，所以其实返回f[x]=find(f[x])时，f[f[x]]就是祖宗。

所以其实就是这样一张图：

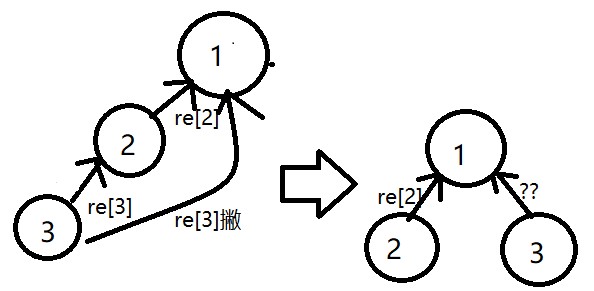
然后放到这个题上，不难发现r[x]=(r[x]+r[f[x]])%3。

大胆猜想，无需证明！！

然后就是合并：

先放图吧！F1是A的祖宗，F2是B的祖宗。

把A和B合并起来（A的祖宗的父亲定为B的祖宗）本质上就是求r[f1]。

而x是知道了的——当A和B是同类时，x就是0，当A吃B时，x就是1。

所以很显然，r[f1]=(r[b]+x-r[a]+3)%3。（因为有可能出现负数，所以+3后再%3）

大胆猜想，无需证明！！

---

种类并查集：

对于种类并查集不了解的可以下看一下这道较为简单的题——团伙。

了解了种类并查集后，再来看看这道题：用三个并查集分别维护同类，食物，天敌（把f数组开三倍大小——1~n,n+1~2*n,n*2+1~3*n）。

对于每一次数据——

• 当1时：判断如果a的天敌是b或b的天敌是a就ans++，否则就合并（a的同类就是b的同类，a的食物就是b的食物，a的天敌就是b的天敌）
• 当2时：判断如果a和b同种或a的天敌是b就ans++，否则就合并（a的食物是b，a的同类是b的天敌，a的天敌是b的食物）

最后输出答案即可。

//写起来比较简单，思考简单，无挑战难度——by ckw

AC代码

加权并查集：

 #include<iostream>
 #include<cstdio>
 using namespace std;
 const int maxn=;
 int n,k,f[maxn],r[maxn],ans;
 int find(int x){
     if(f[x]==x) return x;
     int fa=find(f[x]);
     r[x]=(r[x]+r[f[x]])%;
     f[x]=fa;
     return fa;
 }
 int main()
 {
     cin>>n>>k;
     for(int i=;i<=n;i++){
         f[i]=i;
     }
     while(k--){
         int a,b,c;
         scanf("%d%d%d",&c,&a,&b);
         if((c==&&a==b)||a>n||b>n){
             ans++;
             continue;
         }
         int fx=find(a);
         int fy=find(b);
         if(c==){
             if(fx==fy&&r[a]!=r[b]){
                 ans++;
                 continue;
             }
             if(fx!=fy){
                 f[fx]=fy;
                 r[fx]=(+r[b]-r[a])%;
             }
             continue;
         }
         if(c==){
             if(fx==fy&&(r[a]+-r[b])%!=){
                 ans++;
                 continue;
             }
             if(fx!=fy){
                 f[fx]=fy;
                 r[fx]=(+r[b]-r[a]+)%;
             }
         }
     }
     cout<<ans;
     return ;
 }

加权并查集

种类并查集（压行大法好）：

 #include<iostream>
 #include<cstdio>
 using namespace std;
 const int maxn=;
 int n,k,f[maxn*],ans;
 int find(int x){return f[x]==x?x:f[x]=find(f[x]);}
 int main()
 {
     cin>>n>>k;
     for(int i=;i<=*n;i++){
         f[i]=i;
     }
     while(k--){
         int a,b,c;
         scanf("%d%d%d",&c,&a,&b);
         if(a>n||b>n){ans++;continue;}
         if(c==) (find(a+n)==find(b)||find(b+n)==find(a))?(ans++):(f[find(a)]=find(b),f[find(a+n)]=find(b+n),f[find(a+n*)]=find(b+n*));
         else (a==b||find(a)==find(b)||find(a)==find(b+n))?(ans++):(f[find(a)]=find(b+*n),f[find(a+n)]=find(b),f[find(a+*n)]=find(b+n));
     }
     cout<<ans;
     return ;
 }

种类并查集

//NOI2001 Day1 t1