Codeforces 919E Congruence Equation ( 数论 && 费马小定理 )

题意 : 给出数 x （1 ≤ x ≤ 10^12 ），要求求出所有满足 1 ≤ n ≤ x 的 n 有多少个是满足 n*a^n  = b ( mod p )

分析 :

首先 x 的范围太大了，所以使用枚举进行答案的查找是行不通的

观察给出的同余恒等式，发现这个次方数 n 毫无规律

自然想到化成费马小定理的形式

令 n = i*(p-1)+j

式子化成

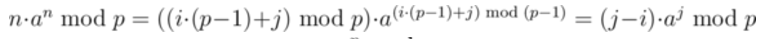
根据费马小定理不难证明(猜???)周期为 p*(p-1)

==> 来自 Tutorial，反正我是不知道怎么证，貌似评论下面有大神用欧拉函数来证

有一个点要提前说一下，我们观察等式中间部分的指数部分

发现如果 j == 0 的话那么在模 p-1 意义下 n 就会变成 0

但是题目给出的范围 n 是不允许为 0 的，所以等等解法里面会把 j == 0 用 j == p-1 代替

然后将刚刚得出的化简结果代回题目原式，于是就可以枚举 j （范围是 1~p-1）来得到 i

此时的得出来的 i 和 j 都是刚刚好满足原式的，于是可得满足原式的最小 n

因为周期是 p*(p-1) 所以后面更大的满足题意的 n 应该为 n+k*[p*(p-1)]，而这里我们不加上周期，故得最小

又因为得知周期为 p*（p-1）所以答案的贡献应该为 ( x - n ) / [p*(p-1)] ==> x > n

#include<bits/stdc++.h>
#define LL long long
using namespace std;

LL pow_mod(LL a, LL b, LL p)
{
    LL ret = ;
    while(b){
        ) ret = (ret * a) % p;
        a = (a * a) % p;
        b >>= ;
    }
    return ret;
}

LL Fermat(LL a, LL p)
{ , p); }

int main(void)
{
    LL a, b, x, p;
    while(~scanf("%I64d %I64d %I64d %I64d", &a, &b, &p, &x)){
        LL ans = ;
        ; j<=p-; j++){
            LL y = b * Fermat(pow_mod(a, j, p), p) % p;
            LL Min_N = (p-) * ((j - y + p)%p) + j;
            if(Min_N > x) continue;
            ans += (x - Min_N) / (p*(p-)) + 1LL;
        }
        printf("%I64d\n", ans);
    }
    ;
}