Password

Description

Rivest是密码学专家。近日他正在研究一种数列E = {E[1],E[2],……,E[n]}，

且E[1] = E[2] = p（p为一个质数），E[i] = E[i-2]*E[i-1] （若2<i<=n）。

例如{2,2,4,8,32,256,8192,……}就是p = 2的数列。在此基础上他又设计了一种加密算法，该算法可以通过一个密钥q (q < p)将一个正整数n加密成另外一个正整数d，计算公式为：d = E[n] mod q。现在Rivest想对一组数据进行加密，但他对程序设计不太感兴趣，请你帮助他设计一个数据加密程序。

Input

第一行读入m，p。其中m表示数据个数，p用来生成数列E。 以下有m行，每行有2个整数n，q。n为待加密数据，q为密钥。 数据范围: 0 < p n< 2^31 0 < q < p 0 < m <= 5000。

Output

将加密后的数据按顺序输出到文件 第i行输出第i个加密后的数据。 输入样例1 2 7 4 5 4 6 输入样例2 4 7 2 4 7 1 6 5 9 3

Sample Input

输入样例1

2 7

4 5

4 6

输入样例2

4 7

2 4

7 1

6 5

9 3

Sample Output

输出样例1

3

1

输出样例2

3

0

1

1

时空限制

1s，64MB

【题解】

      我心中的题目难度排名：数学>玄学>信息学……千古难题数学题，考试的时候刚开始连式子都没推，直接暴力递推骗来49分。后来一直在打大模拟，最后临交卷回来看一眼好像是斐波那契，起码应该拿矩阵快速幂和普通快速幂搞一搞，但是没有时间了就没有打。

欧拉定理，我的理解就是用来降幂，不过这道题好像模了phi[c]之后并没有加phi[c],此等天机本蒟蒻不明觉厉。这个式子推一推就发现p的指数是斐波那契数列，但是斐波那契数列增长很快，所以只能用欧拉定理降幂。具体做法是预处理或直接求q的欧拉函数，把它作为求斐波那契数列的矩阵快速幂里的模数，然后得到降幂后的指数再普通快速幂求p的幂。

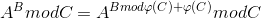
结合快速幂和欧拉定理，这道题大概并不太难。但是在考场上一是没有仔细想，二来也根本没有降幂的意识。数论就像英语音标一样，学了一遍又一遍，还是忘的多会的少。改题的过程更痛苦，几乎是重学欧拉函数(欧拉定理我学过吗？)，原来学的数论只为了做那么两三道题，过后连点定义都说不明白。提高数学水平，是迫在眉睫的问题了。

#include<iostream>
#include<cstdio>
#include<cstring>
#include<cmath>
#define ll long long
using namespace std;
const int sj=;
int m;
ll n,p,q,temp,k,phi[sj],s[sj],ge;
bool v[sj];
void prime(ll x)
{
     for(ll i=;i<x;i++)
     {
        if(!v[i])
        {
           s[ge++]=i;
           phi[i]=i-;
        }
        for(ll j=;j<ge&&i*s[j]<x;j++)
        {
           ll mb=i*s[j];
           v[mb]=;
           if(i%s[j]==)
           {
              phi[mb]=phi[i]*s[j];
              break;
           }
           else phi[mb]=phi[i]*(s[j]-);
        }
     }
     phi[]=;
}
ll fb(ll x,ll y)
{
     ll a[][]={},ans[][]={},f[][]={};
     a[][]=a[][]=a[][]=ans[][]=ans[][]=;
     while(x)
     {
        if(x&)
        {
            memset(f,,sizeof(f));
            for(int i=;i<;i++)
              for(int j=;j<;j++)
                for(int l=;l<;l++)
                  f[i][j]+=ans[i][l]*a[l][j]%y;
            memcpy(ans,f,sizeof(f));
        }
        x>>=;
        memset(f,,sizeof(f));
        for(int i=;i<;i++)
          for(int j=;j<;j++)
            for(int l=;l<;l++)
              f[i][j]+=a[i][l]*a[l][j]%y;
        memcpy(f,a,sizeof(a));
     }
     memset(f,,sizeof(f));
     memset(a,,sizeof(a));
     f[][]=;
     f[][]=;
     for(int i=;i<;i++)
       for(int j=;j<;j++)
         for(int l=;l<;l++)
           a[i][j]+=f[i][l]*ans[l][j]%y;
     return a[][]%y;
}
ll ph(ll x)
{
    if(x<sj) return phi[x];
    ll temp=x;
    for(ll i=;i*i<=x;i++)
       if(x%i==)
       {
          temp=temp-temp/i;
          while(x%i==)
            x/=i;
       }
    if(x>)
      temp=temp-temp/x;
    return temp;
}
ll ksm(ll x,ll y,ll z)
{
    x%=z;
    ll jg=;
    while(y)
    {
       if(y&) jg=jg*x%z;
       x=x*x%z;
       y>>=;
    }
    return jg%z;
}
int main()
{
    prime(sj-);
    scanf("%d%lld",&m,&p);
    for(int i=;i<=m;i++)
    {
       scanf("%lld%lld",&n,&q);
       printf("%lld\n",ksm(p,fb((n-),ph(q)),q));
    }
    return ;
}

password