MLlib--SVD算法

转载请标明出处http://www.cnblogs.com/haozhengfei/p/4db529fa9f4c042673c6dc8218251f6c.html

---

SVD算法

1.1什么是SVD？

   降维的两种方式：PCA（主成分分析）    SVD

   SVD算法：矩阵奇异值分解算法，一种降维算法

1.2矩阵的深入理解

   在一个线性空

间中，只要我们选定一组基，那么对于任何一个线性变换

，都能够用一个确定的矩阵来加以描述，

就如同一个对象可能有多个引用名字不同，所以一组相似矩阵都是一个线性变换在不同的组基的描述

 

特征值与特征向量

    Ax=λx    其中A为矩阵,λ为特征值，x为特征向量，矩阵是线性空间里的变换的描述。

   矩阵A与向量相乘，本质上对向量x进行一次线性转换（旋转或拉伸），而该转换的效果为常数c乘以向量x，当我们求特征值与特征向量的时候，就是为了求矩阵A能使哪些向量（特征向量）只发生拉伸，而拉伸的程度，自然就是特征值λ了。

    特征值分解可以得到特征值与特征向量，特征值表示的是这个特征到底有多重要，而特征向量表示这个特征是什么，不过，特征值分解也有很多的局限，比如说变换的矩阵必须是方阵（n*n）。

    通过特征值分解得到的前N个特征向量，那么就对应了这个矩阵最主要的N个变化方向。我们利用这前N个变化方向，就可以近似这个矩阵（变换）。也就是说：提取这个矩阵最重要的特征。

1.3SVD提取矩阵的特征，解决以上的局限

• 假设A是一个m∗n阶矩阵，如此则存在一个分解使得如下：

 

其中U是m×m阶矩阵；Σ是m×n阶非负实数对角矩阵；而VT，即V的共轭转置，是n×n阶矩阵。这样的分解就称作M的奇异值分解。Σ对角线上的元素Σi,i即为M的奇异值。而且一般来说，我们会将Σ上的值按从大到小的顺序排列。

 

问题：将一个矩阵分解为三个矩阵相乘，但是这三个矩阵的负责程度一点不必原来的A矩阵小，甚至更复杂，为什么要将原来的矩阵分解为三个矩阵呢，这和降纬有什么关系呢？

 

   当我们把矩阵Σ里的奇异值按从大到小的顺

序排列以后，很容易发现，奇异值σ减小的速度特别快。在很

多时候，前10%甚至前1%的奇异值的和就占了全部奇异值和

的99%以上。换句话说，大部分奇异值都很小，基本没什么用

。

于是，SVD也可以这么写：

   这样左边的大矩阵，就能用右边的三个小矩阵表示了，生产中

这三个小矩阵的规模加起来也远小于原本的矩阵A，从而达到

降纬的目的。

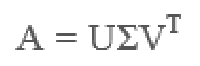
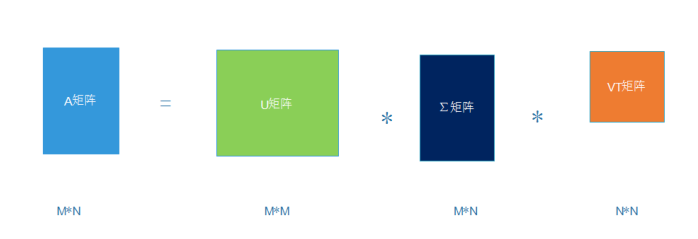
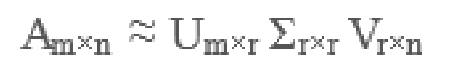
1.4SVD_code

train

SVD_new

代码示例

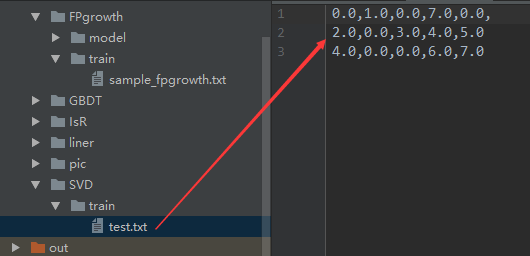
 import org.apache.log4j.{Level, Logger}
 import org.apache.spark.{SparkConf, SparkContext}
 import org.apache.spark.mllib.linalg
 import org.apache.spark.mllib.linalg.{Matrix, SingularValueDecomposition, Vectors}
 import org.apache.spark.mllib.linalg.distributed.RowMatrix
 import org.apache.spark.rdd.RDD

 /**
   * Created by hzf
   */
 object SVD_new {
     //  E:\IDEA_Projects\mlib\data\SVD\train\test.txt E:\IDEA_Projects\mlib\data\SVD\model 3 true 1.0E-9d local
     def main(args: Array[String]) {
         Logger.getLogger("org.apache.spark").setLevel(Level.ERROR)
         if (args.length < 6) {
             System.err.println("Usage: SVD <inputPath> <modelPath> <num> <compute> <ignore> <master> [<AppName>]")
             System.exit(1)
         }
         val appName = if (args.length > 6) args(6) else "SVD"
         val conf = new SparkConf().setAppName(appName).setMaster(args(5))
         val sc = new SparkContext(conf)
         val data = sc.textFile(args(0))
         val train: RDD[linalg.Vector] = data.map(sample => {
             Vectors.dense(sample.split(",").map(_.toDouble))
         })
         val mat: RowMatrix = new RowMatrix(train)
         var compute = true
         compute = args(3) match {
             case "true" => true
             case "false" => false
         }
         //第一个参数3意味着取top 3个奇异值，第二个参数true意味着计算矩阵U，第三个参数意味小于1.0E-9d的奇异值将被抛弃
         val svd: SingularValueDecomposition[RowMatrix, Matrix] = mat.computeSVD(args(2).toInt, compute);
         val u = svd.U;
         //矩阵U
         val s = svd.s
         //奇异值
         val v = svd.V //矩阵V
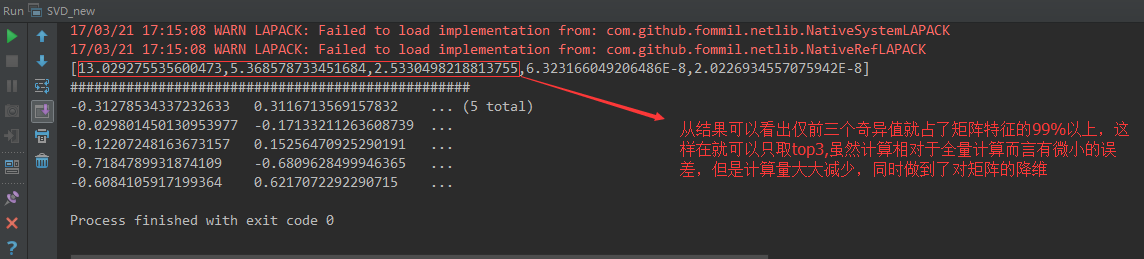
         println(s);
         println("#" * 50);
         println(v);
     }
 }

设置运行参数

1. E:\IDEA_Projects\mlib\data\SVD\train\test.txt E:\IDEA_Projects\mlib\data\SVD\model 3true1.0E-9d local