Coursera 机器学习笔记（六）

主要为第八周内容：聚类(Clustering)、降维

聚类是非监督学习中的重要的一类算法。相比之前监督学习中的有标签数据，非监督学习中的是无标签数据。非监督学习的任务是对这些无标签数据根据特征找到内在结构。聚类就是通过算法把数据分成不同的簇（点集），k均值算法是其中一种重要的聚类算法。

K均值算法

K-均值是一个迭代算法，假设我们想要将数据聚类成 n 个组，其方法为:

1.首先选择 K 个随机的点，称为聚类中心（cluster centroids）

2. 对于数据集中的每一个数据，按照距离 K 个中心点的距离，将其与距离最近的中心点关联起来，与同一个中心点关联的所有点聚成一类

3. 计算每一个组的平均值，将该组所关联的中心点移动到平均值的位置

4. 重复步骤 2-4 直至中心点不再变化

代价函数

K均值算法的代价函数是所有的数据点与其所关联的聚类中心点之间的距离之和，又称为畸变函数(Distortion function)

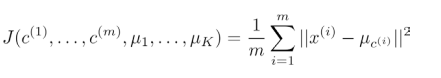
其中u(i)代表x(i)最近的聚类中心点。

我们的优化目标就是最小化代价函数。

随机初始化

做法：

1.我们应该选择 K<m，即聚类中心点的个数要小于所有训练集实例的数量
2. 随机选择 K 个训练实例，然后令 K 个聚类中心分别与这 K 个训练实例相等

取决于初始化，K均值可能会停留在一个局部最小值。K 较小时，解决这个问题的办法是多次运行k均值算法，每次都随机初始化，选择其中代价函数最小的结果。

K较大时，多次随机初始化，不会有明显改善。

聚类数K

取决于不同的实际情况，人工进行选择聚类数。如衣服制造：可以按照身材聚类，有S,M,L 或者 XS,S,M,L,XL等。

有一种方法叫做肘部法则：改变K值，计算相应的代价函数，画出k与代价函数的曲线：

如果得到一张类似的图，那么将"肘点"作为k值选择是一种合理办法。不过通常比较难出现这种肘部图。

降维也是机器学习算法的重要部分。为什么需要降维？一、数据压缩，减少特征；二、数据可视化，显然后50维的数据很难想象出它的可视化图像，降低至2维、3维即可。主成分分析(PCA)是最常见的降维算法。

主成分分析(PCA)

主要成分分析(PCA)问题的描述：

1.问题是要将 n 维数据降至 k 维

2.目标是找到向量 u(1),u(2),...,u(k)使得总的投射误差最小

如二维到一维：

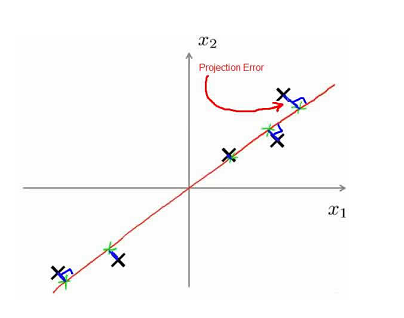
与线性回归相比，主要成分分析最小化的是投射误差，而线性回归尝试的是最小化预测误差。线性回归的目的是预测结果，而主要成分分析不作任何预测。

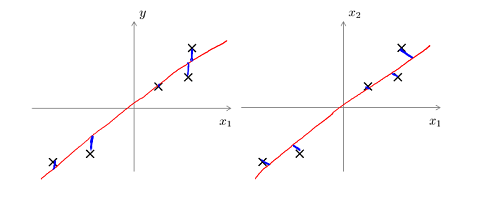
PCA技术的好处是对数据进行降维的处理，将"主元"向量的重要性排序，根据需要选取前面最重要的部分，从而达到降维的目的，同时又最大程度保留了原有数据的信息。另一个好处是完全无参数限制，最后只与数据有关，与用户是独立的。

算法

步骤:

第一步：均值归一化。

第二步：计算协方差矩阵Σ

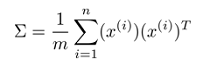
第三步：计算协方差矩阵Σ的特征向量

在matlab中可以利用奇异值分解(singular value decomposition), [U, S, V] = svd(sigma)。

对于一个 n×n 维度的矩阵，上式中的 U 是一个具有与数据之间最小投射误差的方向向量构成的矩阵。如果我们希望将数据从 n 维降至 k 维，我们只需要从 U 中选取前 K 个向量，获得一个 n×k 维度的矩阵，我们用 Ureduce 表示，然后通过如下计算获得要求的新特征向量Z(i)：其中 x 是 n×1 维的，因此结果为 k×1 维度。

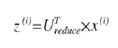
主成分数量

主成分分析的代价函数是平均均方误差：

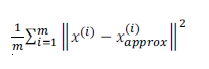
训练集的方差：

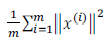
我们希望在平均均方误差与训练集方差的比例尽可能小的情况下选择尽可能小的 K 值。如果我们希望这个比例小于 1%，就意味着原本数据的偏差有 99%都保留下来了，如果我们选择保留 95%的偏差，便能非常显著地降低模型中特征的维度了。

我们可以先令 K=1，然后进行主要成分分析，获得 Ureduce 和 z，然后计算比例是否小于1%。如果不是的话再令 K=2，如此类推，直到找到可以使得比例小于 1%的最小 K 值（原因是各个特征之间通常情况存在某种相关性）。

更好的办法是利用matlab中奇异值分解，[U, S, V] = svd(sigma)中的S

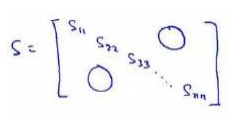
，我们可以使用这个矩阵来计算平均均方误差与训练集方差的比例：

重建

PCA降维方程是：

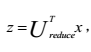
则可由相反方程重建x：

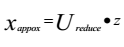
如图所示：

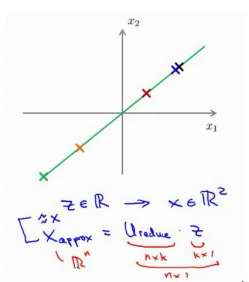
建议

一般而言,PCA使用步骤是先降维；然后降维后的特征进行训练，学习算法；在预测时，根据之前PCA的Ureduce将输入特征x转换为相应z,然后再进行预测。

一个常见的错误情况是：将PCA其用于减少过拟合（减少了特征的数量）。原因在于主要成分分析只是近似地丢弃掉一些特征，它并不考虑任何与结果变量有关的信息，因此可能会丢失非常重要的特征。

另一个常见的错误是，默认地将主要成分分析作为学习过程中的一部分，这虽然很多时候有效果，最好还是从所有原始特征开始，只在有必要的时候（算法运行太慢或者占用太多内存）才考虑采用主要成分分析。