机器学习 —— 基础整理（八）循环神经网络的BPTT算法步骤整理；梯度消失与梯度爆炸

网上有很多Simple RNN的BPTT（Backpropagation through time，随时间反向传播）算法推导。下面用自己的记号整理一下。

我之前有个习惯是用下标表示样本序号，这里不能再这样表示了，因为下标需要用做表示时刻。

典型的Simple RNN结构如下：

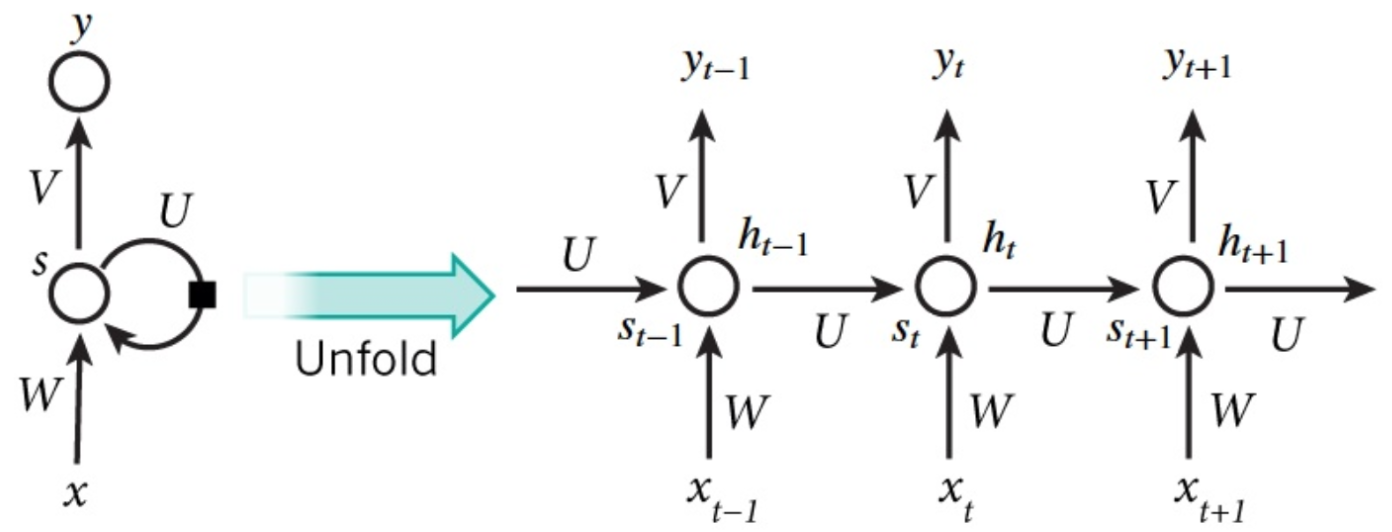
图片来源：[3]

约定一下记号：

输入序列 $\textbf x_{(1:T)} =(\textbf x_1,\textbf x_2,...,\textbf x_T)$ ；

标记序列 $\textbf y_{(1:T)} =(\textbf y_1,\textbf y_2,...,\textbf y_T)$ ；

输出序列 $\hat{\textbf y}_{(1:T)} =(\hat{\textbf y}_1,\hat{\textbf y}_2,...,\hat{\textbf y}_T)$ ；

隐层输出 $\textbf h_t\in\mathbb R^H$ ；

隐层输入 $\textbf s_t\in\mathbb R^H$ ；

过softmax之前输出层的输出 $\textbf z_t$ 。

（一）Simple RNN的BPTT

那么对于Simple RNN来说，前向传播过程如下（省略了偏置）：

$$\textbf s_t=U\textbf h_{t-1}+W\textbf x_t$$

$$\textbf h_t=f (\textbf s_t)$$

$$\textbf z_t=V\textbf h_t$$

$$\hat{\textbf y}_t=\text{softmax}(\textbf z_t)$$

其中 $f$ 是激活函数。注意，三个权重矩阵在时间维度上是共享的。这可以理解为：每个时刻都在执行相同的任务，所以是共享的。

既然每个时刻都有输出 $\hat{\textbf y}_t$ ，那么相应地，每个时刻都会有损失。记 $t$ 时刻的损失为 $\mathcal L_t$ ，那么对于样本 $\textbf x_{(1:T)}$ 来说，损失 $\mathcal L$ 为

$$\mathcal L=\sum_{t=1}^T\mathcal L_t$$

使用交叉熵损失函数，那么

$$\mathcal L_t=-\textbf y_t^{\top}\log\hat{\textbf y}_t$$

一、 $\mathcal L$ 对 $V$ 的梯度

下面首先求取 $\mathcal L$ 对 $V$ 的梯度。根据chain rule：$\dfrac{\partial \textbf z}{\partial \textbf x}=\dfrac{\partial \textbf y}{\partial \textbf x}\dfrac{\partial \textbf z}{\partial \textbf y}$ 、$\dfrac{\partial z}{\partial X_{ij}}=(\dfrac{\partial z}{\partial\textbf y})^{\top}\dfrac{\partial\textbf y}{\partial X_{ij}}$ ，有

$$\frac{\partial \mathcal L_t}{\partial V_{ij}}=(\frac{\partial \mathcal L_t}{\partial\textbf z_t})^{\top}\frac{\partial\textbf z_t}{\partial V_{ij}}$$

这里其实和BP是一样的，前一项相当于是误差项 $\delta$ ，后一项等于

$$\frac{\partial \textbf z_t}{\partial V_{ij}}=\frac{\partial V\textbf h_t}{\partial V_{ij}}=(0,...,[\textbf h_t]_j,...,0)^{\top}$$

只有第 $i$ 行非零，$[\textbf h_t]_j$ 是指 $\textbf h_t$ 的第 $j$ 个元素。参考上一篇博客的结尾部分，可知前一项等于

$$\frac{\partial \mathcal L_t}{\partial\textbf z_t}=\hat{\textbf y}_t-\textbf y_t$$

所以有

$$\frac{\partial \mathcal L_t}{\partial V_{ij}}=[\hat{\textbf y}_t-\textbf y_t]_i[\textbf h_t]_j$$

从而有

$$\frac{\partial \mathcal L_t}{\partial V}=(\hat{\textbf y}_t-\textbf y_t)\textbf h_t^{\top}=(\hat{\textbf y}_t-\textbf y_t)\otimes \textbf h_t$$

向量外积是矩阵的Kronecker积在向量下的特殊情况。因此，

$$\frac{\partial \mathcal L}{\partial V}=\sum_{t=1}^T(\hat{\textbf y}_t-\textbf y_t)\otimes \textbf h_t$$

二、 $\mathcal L$ 对 $U$ 的梯度

继续求取 $\mathcal L$ 对 $U$ 的梯度。在求 $\frac{\partial \mathcal L_t}{\partial U}$ 时，需要注意到一个事实，那就是不光 $t$ 时刻的隐状态与 $U$ 有关，之前所有时刻的隐状态都与 $U$ 有关。

图片来源：[1]

所以，根据chain rule：

$$\frac{\partial \mathcal L_t}{\partial U}=\sum_{k=1}^t\frac{\partial\textbf s_k}{\partial U}\frac{\partial \mathcal L_t}{\partial\textbf s_k}$$

下面使用和之前类似的套路求解：先求对一个矩阵一个元素的梯度。

$$\frac{\partial \mathcal L_t}{\partial U_{ij}}=\sum_{k=1}^t(\frac{\partial \mathcal L_t}{\partial\textbf s_k})^{\top}\frac{\partial\textbf s_k}{\partial U_{ij}}$$

前一项先定义为 $\delta_{t,k}=\dfrac{\partial \mathcal L_t}{\partial\textbf s_k}$ ，对于后一项：

$$\frac{\partial\textbf s_k}{\partial U_{ij}}=\frac{\partial(U\textbf h_{k-1}+W\textbf x_k)}{\partial U_{ij}}=(0,...,[\textbf h_{k-1}]_j,...,0)^{\top}$$

只有第 $i$ 行非零，$[\textbf h_{k-1}]_j$ 是指 $\textbf h_{k-1}$ 的第 $j$ 个元素。现在来求解 $\delta_{t,k}=\dfrac{\partial \mathcal L_t}{\partial\textbf s_k}$ ，使用上篇文章求 $\delta^{(l)}$ 的套路：

$$\begin{aligned}\delta_{t,k}&=\frac{\partial \mathcal L_t}{\partial\textbf s_k}\\&=\frac{\partial \textbf h_k}{\partial\textbf s_{k}}\frac{\partial \textbf s_{k+1}}{\partial\textbf h_{k}}\frac{\partial \mathcal L_t}{\partial\textbf s_{k+1}}\\&=\text{diag}(f'(\textbf s_k))U^{\top}\delta_{t,k+1}\\&=f'(\textbf s_{k})\odot (U^{\top}\delta_{t,k+1})\end{aligned}$$

一种特殊情况是当 $\delta_{t,t}$ ，有

$$\begin{aligned}\delta_{t,t}&=\frac{\partial \mathcal L_t}{\partial\textbf s_t}\\&=\frac{\partial \textbf h_t}{\partial\textbf s_t}\frac{\partial \textbf z_t}{\partial\textbf h_t}\frac{\partial \mathcal L_t}{\partial\textbf z_t}\\&=\text{diag}(f'(\textbf s_{t}))V^{\top}(\hat{\textbf y}_t-\textbf y_t)\\&=f'(\textbf s_{t})\odot (V^{\top}(\hat{\textbf y}_t-\textbf y_t))\end{aligned}$$

所以，

$$\frac{\partial \mathcal L_t}{\partial U_{ij}}=\sum_{k=1}^t[\delta_{t,k}]_i[\textbf h_{k-1}]_j$$

$$\frac{\partial \mathcal L_t}{\partial U}=\sum_{k=1}^t\delta_{t,k}\textbf h_{k-1}^{\top}=\sum_{k=1}^t\delta_{t,k}\otimes\textbf h_{k-1}$$

因此，

$$\frac{\partial \mathcal L}{\partial U}=\sum_{t=1}^T\sum_{k=1}^t\delta_{t,k}\otimes\textbf h_{k-1}$$

三、$\mathcal L$ 对 $W$ 的梯度

观察 $\textbf s_t=U\textbf h_{t-1}+W\textbf x_t$ 这个式子，不难发现只要把刚刚推导的结果做一下简单的替换就可以直接得到新的结果：

$$\frac{\partial \mathcal L_t}{\partial W}=\sum_{k=1}^t\delta_{t,k}\otimes\textbf x_{k}$$

$$\frac{\partial \mathcal L}{\partial W}=\sum_{t=1}^T\sum_{k=1}^t\delta_{t,k}\otimes\textbf x_{k}$$

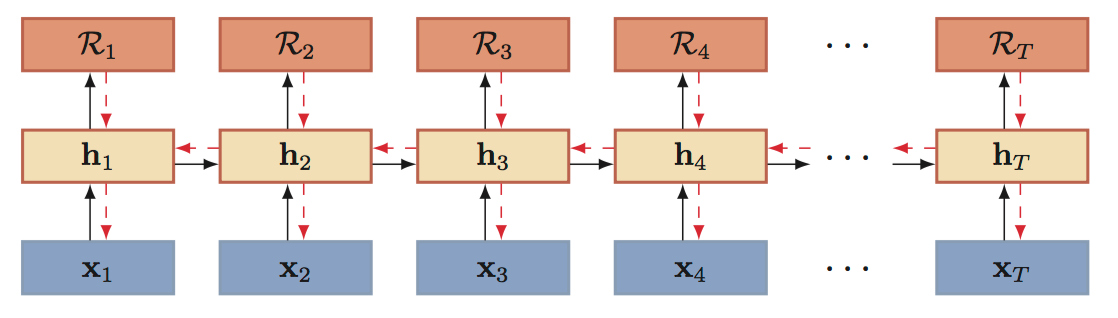
总的来说，没有写什么insightful的东西，就是记录一下而已。使用的套路都是BP中使用的（其实就是很基本的chain rule）。但是需要注意的是，这里实际上是在时间维度上的展开。如果是跟普通的神经网络那样构造多个隐层，则需要在“纵向”上继续扩展，形成所谓的深度RNN。因为Theano等自动求导工具的存在，所以如果只是为了编程的话，很多情况下其实也不太需要手推了。

深度双向RNN。图片来源：[2]

（二）梯度消失（gradient vanishing）

我们考察一下下面这个梯度：

$$\frac{\partial \mathcal L_t}{\partial U}=\frac{\partial \textbf h_t}{\partial U}\frac{\partial \hat{\textbf y}_t}{\partial \textbf h_t}\frac{\partial \mathcal L_t}{\partial \hat{\textbf y}_t}$$

这里的 $\dfrac{\partial \textbf h_t}{\partial U}$ 比较麻烦，是因为各个时刻共享了参数：$\textbf h_t$ 这个参数是和 $\textbf h_{t-1}$ 、$U$ 有关的，而 $\textbf h_{t-1}$ 又和 $\textbf h_{t-2}$ 、$U$ 有关。所以参照 [5] ，可以写成以下形式（读 [5] 的时候需要注意其前向传播过程和 [4] 一样，与本文是有区别的，但在这里不妨碍理解）：

$$\frac{\partial \mathcal L_t}{\partial U}=\sum_{k=1}^t\frac{\partial \textbf h_k}{\partial U}\frac{\partial \textbf h_t}{\partial \textbf h_k}\frac{\partial \hat{\textbf y}_t}{\partial \textbf h_t}\frac{\partial \mathcal L_t}{\partial \hat{\textbf y}_t}$$

其中，

$$\begin{aligned}\frac{\partial \textbf h_t}{\partial \textbf h_k}&=\prod_{i=k+1}^t\frac{\partial \textbf h_i}{\partial \textbf h_{i-1}}\\&=\prod_{i=k+1}^t\frac{\partial \textbf s_i}{\partial \textbf h_{i-1}}\frac{\partial f(\textbf s_i)}{\partial \textbf s_i}\\&=\prod_{i=k+1}^tU^{\top}\text{diag}{f'(\textbf s_i)}\end{aligned}$$

从这个式子可以看出，当使用tanh或logistic激活函数时，由于导数值分别在0到1之间、0到1/4之间，所以如果权重矩阵 $U$ 的范数也不很大，那么经过 $t-k$ 次传播后，$\dfrac{\partial \textbf h_t}{\partial \textbf h_k}$ 的范数会趋于0，也就导致了梯度消失问题。其实从上面误差项的表达式也可以看出，$\delta_{t,k}$ 与 $\delta_{t,k+1}$ 是乘一个导函数的关系，这个导函数值域在0到1之间（tanh）、0到1/4之间（logistic），那么随着时间的累积，当然会造成梯度消失问题。

为了缓解梯度消失，可以使用ReLU、PReLU来作为激活函数，以及将 $U$ 初始化为单位矩阵（而不是用随机初始化）等方式。

（普通的前馈深层神经网络也会存在梯度消失，只不过那里是“纵向”上的。）

也就是说，虽然Simple RNN从理论上可以保持长时间间隔的状态之间的依赖关系，但是实际上只能学习到短期依赖关系。这就造成了“长期依赖”问题。打个比方，你对着模型说了一大段话，“你好，我叫小明，balabala……，很高兴认识你”。模型听完之后回答你：“很高兴认识你，你叫什么？我叫小红。”——模型已经忘了你叫什么了。

需要通过带LSTM单元的RNN来缓解梯度消失问题，现在一般把使用LSTM单元的RNN就直接叫LSTM了。LSTM单元引入了门机制（Gate），通过遗忘门、输入门和输出门来控制流过单元的信息。我们知道，Simple RNN之所以有梯度消失是因为误差项之间的相乘关系；如果用LSTM推导，会发现这个相乘关系变成了相加关系，所以可以缓解梯度消失。

 （三）梯度爆炸（gradient exploding）

而对于梯度爆炸问题，通常就是使用比较简单的策略，也就是gradient clipping梯度裁剪：如果在一次迭代中各个权重的梯度平方和大于某个阈值，那么为避免权重的变化值太大，求一个缩放因子（阈值除以平方和），将所有的梯度乘以这个因子。TensorFlow里提供了很多种梯度裁剪的函数，直接看API吧。

参考：

[1] 《神经网络与深度学习讲义》

[2] Recurrent Neural Networks Tutorial, Part 1 – Introduction to RNNs

Recurrent Neural Networks Tutorial, Part 3 – Backpropagation Through Time and Vanishing Gradients

[3] BPTT算法推导

[4] On the difficulty of training RNN

[5] Rucurrent nets and LSTM

[6] 知乎：deep bidirectional RNN +LSTM 用于癫痫检测的疑问？

[7] caffe里的clip gradient是什么意思？