归并排序（MergeSort）和快速排序(QuickSort)的一些总结问题

归并排序（MergeSort）和快速排序(QuickSort)都是用了分治算法思想。

所谓分治算法，顾名思义，就是分而治之，就是将原问题分割成同等结构的子问题，之后将子问题逐一解决后，原问题也就得到了解决。

同时，归并排序（MergeSort）和快速排序(QuickSort)也代表了两类分治算法的思想。

对于归并排序，我们对于待处理序列怎么分的问题上并没有太多关注，仅仅是简单地一刀切，将整个序列分成近乎均匀的两份，然后将子序列进行同样处理。但是，我们更多的关注点在于怎么把分开的部分合起来，也就是merge的过程。

对于快速排序来说，我们则是花了很大的功夫放在了怎么分这个问题上，我们设定了枢轴（标定点），然后通过partition的过程将这个枢轴放在合适的位置，这样我们就不用特别关心合起来的过程，只需要一步一步地递归下去即可。

下面说两个从归并排序和快速排序所衍生出来的问题。

1）关于求一个数组中逆序对数量的问题

---

在一个数组中，

随机取出两个元素，例如取出的是2和3，根据它们原来的位置顺序看，它们是有序的，那么这个数字对就称为顺序对。

当取出的是2和1时，根据它们原来的位置顺序看，2排在1的前面，而2却比1要大，这样的数字对称为逆序对。

一个数组中逆序对的数量，可以用来衡量一个数组的有序程度。

那么怎么求一个数组中逆序对的数量呢？

一个最简单的方法就是暴力解法：考察每一个数字对（使用双重循环），算法复杂度为O（n²）

我们还可以使用归并算法进行考察逆序对的个数，使得我们的算法复杂度到达O（nlog₂n）级别的。

使用归并算法，最关键的是归并的过程。

举个例子：

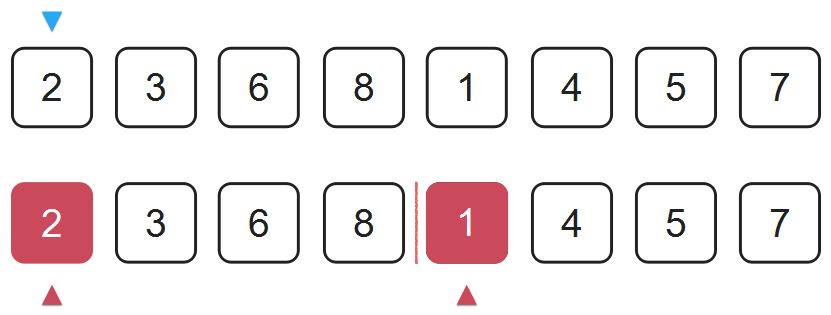
在这个序列的归并排序中，归并过程我们首先比较紫色部分的2和1的大小，由于1比2小，所以我们把1放到最前端的位置。

由于每个子序列在归并之前都是有序的，既然1比2小，那么1也一定比第一个子序列中2后面的所有元素小，换句话说，这个1比前面子序列中2以及2之后的所有元素都构成了逆序对。所以在将1放到整个序列最前端的过程中，我们就可以给逆序对的计数器加上4。

接下来比较2和4：

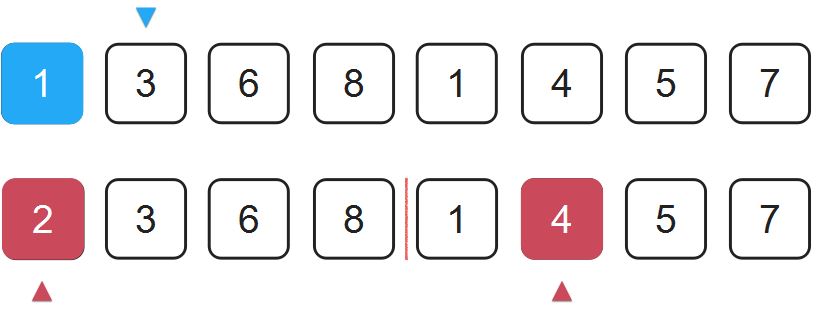
这里2比4要小，那么就把2放到1的后面。

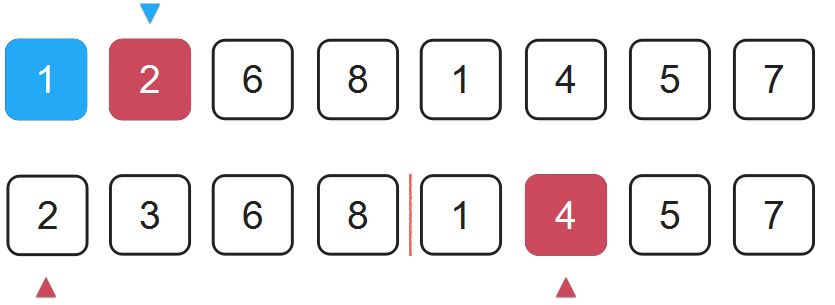
2比4小，还意味着2比4后面的所有元素都要小。那么此时就没有构成任何逆序对。计数器不动，继续归并。

以此类推。

这样我们就把暴力解法中的一对一对的比较变成了一组一组的比较。

代码：

package com.mergeSort;

import java.util.*;

public class InversionCount{

    // 我们的算法类不允许产生任何实例
    private InversionCount(){}

    // merge函数求出在arr[l...mid]和arr[mid+1...r]有序的基础上, arr[l...r]的逆序数对个数
    private static long merge(int[] arr, int l, int mid, int r) {

        int[] aux = Arrays.copyOfRange(arr, l, r+1);//注意复制后的数组元素包括前索引位置的元素，不包括后索引位置的元素

        // 初始化逆序数对个数 res = 0
        long res = 0L;
        // 初始化，i指向左半部分的起始索引位置l；j指向右半部分起始索引位置mid+1
        int i = l, j = mid+1;
        for( int k = l ; k <= r; k ++ ){

            if( i > mid ){  // 如果左半部分元素已经全部处理完毕
                arr[k] = aux[j-l];//注意有l个偏移量
                j ++;
            }
            else if( j > r ){   // 如果右半部分元素已经全部处理完毕
                arr[k] = aux[i-l];
                i ++;
            }
            else if( aux[i-l]<=aux[j-l] ){  // 左半部分所指元素 <= 右半部分所指元素
                arr[k] = aux[i-l];
                i ++;
            }
            else{   // 右半部分所指元素 < 左半部分所指元素
                arr[k] = aux[j-l];
                j ++;
                // 此时, 因为右半部分k所指的元素小
                // 这个元素和左半部分的所有未处理的元素都构成了逆序数对
                // 左半部分此时未处理的元素个数为 mid - i + 1
                res += (long)(mid - i + 1);
            }
        }

        return res;
    }

    // 求arr[l..r]范围的逆序数对个数
    // 思考: 归并排序的优化可否用于求逆序数对的算法? :)
    private static long solve(int[] arr, int l, int r) {

        if (l >= r)
            return 0L;

        int mid = l + (r-l)/2;
        // 求出 arr[l...mid] 范围的逆序数
        long res1 = solve(arr, l, mid);
        // 求出 arr[mid+1...r] 范围的逆序数
        long res2 = solve(arr, mid + 1, r);
　　　　　//只有每一次merge才会返回逆序数，而最底层的res(即solve()方法的返回值)都为0
　　　　　//所以这一句最后加的总和其实就是每次merge的返回值
        return res1 + res2 + merge(arr, l, mid, r);
    }

    public static long solve(int[] arr){

        int n = arr.length;
        return solve(arr, 0, n-1);
    }

    // 测试 InversionCount
    public static void main(String[] args) {
        int[] arr=new int[]{1,2,3,5,4,4};
        long l=solve(arr);
        System.out.println(l);
        return;
    }
}

2）取出数组（无序）中第n个大的元素

---

最简单的实例就是求数组中的最大值和最小值。这需要我们从头到尾遍历扫描一下即可。时间复杂度为O（n）。

那么怎么求数组中第n个大的元素呢？

容易想到的一个就是给整个数组排一下序，时间复杂度为：O（nlog₂n）。

其实我们可以使用快速排序算法的思想来求解这个问题，来使得时间复杂度达到O（n）级别。

在快速排序中，每一次我们都需要找到一个标定点，然后将这个标定点放到合适的位置，这个合适的位置就是这个元素在排好序后最终应该在的位置。那么从它的索引就能看出它是第几大的元素。

例如，

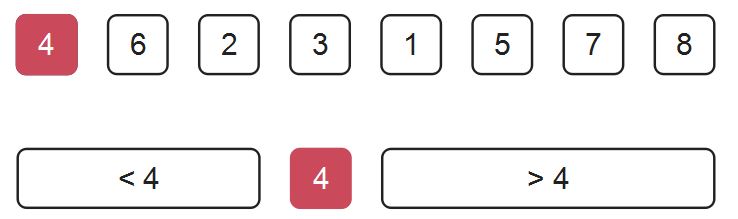
在排完第一个元素时，我们发现一个元素4恰好是第4名，也就是说4这个元素在这个序列中是第4大的。那么现在问题是：请问这个序列第6大的元素是谁？

此时我们就不用去管元素4前面的位置了，只需要递归地去求解元素4后面的元素即可。

同样的，如果问题是：请问这个序列第2大的元素是谁？

那么我们只需要递归地去求解元素4前面的元素即可。

在不太规范的统计下，时间复杂度为：

代码：

package com.quickSort;

import java.util.*;

public class QuickSortWhoBig2 {

    // 我们的算法类不允许产生任何实例
    private QuickSortWhoBig2(){}

    // 对arr[l...r]部分进行partition操作
    // 返回p, 使得arr[l...p-1] < arr[p] ; arr[p+1...r] > arr[p]
    // partition 过程, 和快排的partition一样
    private static int partition(int[] arr, int l, int r){

        int v = arr[l];

        int j = l; // arr[l+1...j] < v ; arr[j+1...i) > v
        for( int i = l + 1 ; i <= r ; i ++ )
            if( arr[i] < v ){
                j ++;
                int tem=arr[i];
                arr[i]=arr[j];
                arr[j]=tem;
            }

        int tem=arr[l];
        arr[l]=arr[j];
        arr[j]=tem;

        return j;
    }

    // 求出nums[l...r]范围里第k小的数
    private static int solve(int[] nums, int l, int r, int k){

        if( l == r )
            return nums[l];

        // partition之后, nums[p]的正确位置就在索引p上
        int p = partition(nums, l, r);

        if( k == p )    // 如果 k == p, 直接返回nums[p]
            return nums[p];
        else if( k < p )    // 如果 k < p, 只需要在nums[l...p-1]中找第k小元素即可
            return solve( nums, l, p-1, k);
        else // 如果 k > p, 则需要在nums[p+1...r]中找第k-p-1小元素
             // 注意: 由于我们传入QuickSortWhoBig2的依然是nums, 而不是nums[p+1...r],
             //       所以传入的最后一个参数依然是k, 而不是k-p-1
            return solve( nums, p+1, r, k );
    }

    // 寻找nums数组中第k小的元素
    // 注意: 在我们的算法中, k是从0开始索引的, 即最小的元素是第0小元素, 以此类推
    // 如果希望我们的算法中k的语意是从1开始的, 只需要在整个逻辑开始进行k--即可, 可以参考solve2
    public static int solve(int nums[], int k) {

        return solve(nums, 0, nums.length - 1, k);
    }

    // 寻找nums数组中第k小的元素, k从1开始索引, 即最小元素是第1小元素, 以此类推
    public static int solve2(int nums[], int k) {

        return QuickSortWhoBig2.solve(nums, k - 1);
    }

    // 测试 QuickSortWhoBig2
    public static void main(String[] args) {
        int[] arr=new int[]{10,9,8,7,6,5,4,3,2,1};
        int n=1;
        for(int i=0;i<10;i++){
            System.out.println("第"+n+"大的元素为："+solve2(arr,n));
            n++;
        }

    }
}

输出结果：