AI学习---基于TensorFlow的案例[实现线性回归的训练]

• 线性回归原理复习

1）构建模型
               |_> y = w1x1 + w2x2 + …… + wnxn + b
        2）构造损失函数
               |_> 均方误差
        3）优化损失
               |_> 梯度下降

• 实现线性回归的训练

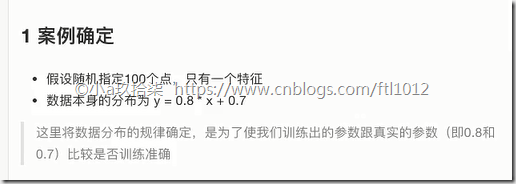
准备真实数据
            100样本
            x 特征值 形状 (100, 1)  100行1列
            y_true 目标值 (100, 1)
            y_true = 0.8x + 0.7    假设特征值和目标值直接的线性关系
        假定x 和 y 之间的关系 满足
            y = kx + b
            k ≈ 0.8 b ≈ 0.7
            流程分析：
            (100, 1) * (1, 1) = (100, 1)
            y_predict = x * weights(1, 1) + bias(1, 1)
            1）构建模型： 矩阵：matmul
                y_predict = tf.matmul(x, weights) + bias
            2）构造损失函数: 平均：reduce_mean  平方: square
                error = tf.reduce_mean(tf.square(y_predict - y_true))
            3）优化损失:  梯度下降的评估器GradientDescentOptimizer
                optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.01).minimize(error)
            5 学习率的设置、步数的设置与梯度爆炸

• 案例确定

• API

• 步骤分析

demo:

import tensorflow as tf
import os

os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'

def linear_regression():
    """
    自实现一个线性回归
    :return:
    """
    # 1）准备数据
    with tf.variable_scope(name_or_scope='prepare_data'):
        X = tf.random_normal(shape=[100, 1], mean=2)
        y_true = tf.matmul(X, [[0.8]]) + 0.7   # [[0.8]] 定义了一个一行一列

    # 2）构造模型
    # 定义模型参数 用 变量
    with tf.variable_scope("create_model"):
        weights = tf.Variable(initial_value=tf.random_normal(shape=[1, 1]))  # 随机产生一个一行一列
        bias = tf.Variable(initial_value=tf.random_normal(shape=[1, 1]))   # 随机产生一个一行一列
        y_predict = tf.matmul(X, weights) + bias

    # 3）构造损失函数： 均方误差
    with tf.variable_scope("loss_function"):
        error = tf.reduce_mean(tf.square(y_predict - y_true))

    # 4）优化损失
    with tf.variable_scope("optimizer"):
        optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.01).minimize(error) # 默认0.01

    # 显式地初始化变量
    init = tf.global_variables_initializer()

    with tf.Session() as sess:

        # 初始化变量
        sess.run(init)
        # 查看初始化模型参数之后的值
        print("训练前模型参数为：权重%f，偏置%f，损失为%f" % (weights.eval(), bias.eval(), error.eval()))
        # 开始训练
        for i in range(10):
            sess.run(optimizer)
            print("训练前模型参数为：权重%f，偏置%f，损失为%f" % (weights.eval(), bias.eval(), error.eval()))

if __name__ == "__main__":
    linear_regression()

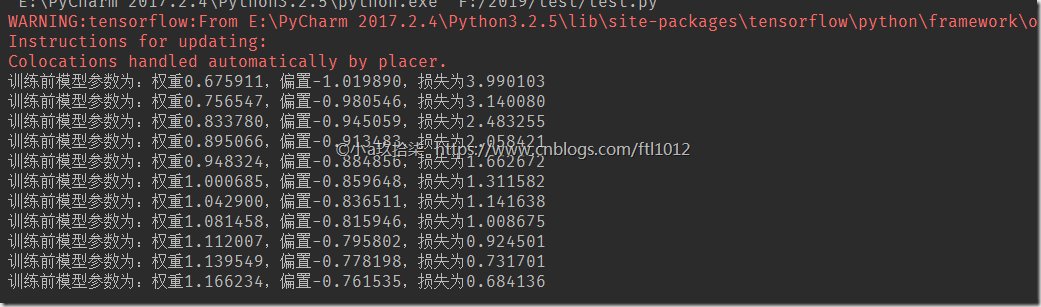
经过上面的训练我们可以发现，在学习率不变的情况下，迭代的次数越多，则效果越好。同理在迭代次数一定的情况下，学习率越高效果越好，但也是有一定限制的。

• 学习率的设置、步数的设置与梯度爆炸

• 变量的trainable设置观察

增加TensorBoard显示

1）创建事件文件
            2）收集变量
            3）合并变量
            4）每次迭代运行一次合并变量
            5）每次迭代将summary对象写入事件文件

变量dashboard显示demo:

import tensorflow as tf
import os

os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'

def linear_regression():
    """
    自实现一个线性回归
    :return:
    """
    # 第一步：
    # 1）准备数据
    X = tf.random_normal(shape=[100, 1], mean=2)
    y_true = tf.matmul(X, [[0.8]]) + 0.7   # [[0.8]] 定义了一个一行一列

    # 2）构造模型
    # 定义模型参数 用 变量
    # trainable=False，的时候则后面的权重会不变，导致损失也不会变化太久，默认True
    weights = tf.Variable(initial_value=tf.random_normal(shape=[1, 1]), trainable=True)  # 随机产生一个一行一列
    bias = tf.Variable(initial_value=tf.random_normal(shape=[1, 1]))   # 随机产生一个一行一列
    y_predict = tf.matmul(X, weights) + bias

    # 3）构造损失函数： 均方误差
    error = tf.reduce_mean(tf.square(y_predict - y_true))

    # 4）优化损失
    optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.01).minimize(error)

    # 显式地初始化变量
    init = tf.global_variables_initializer()

    # 第二步：收集变量
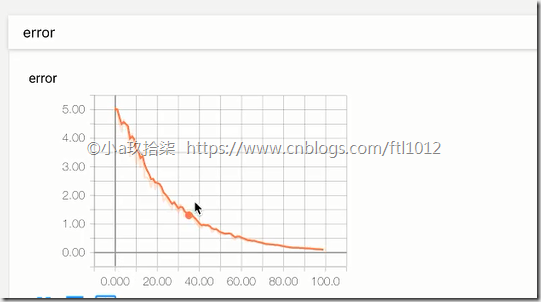
    tf.summary.scalar("error", error)
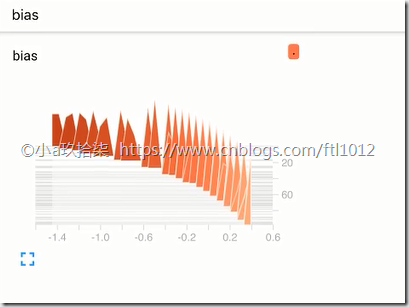
    tf.summary.histogram("weights", weights)
    tf.summary.histogram("bias", bias)

    # 第三步：合并变量
    merged = tf.summary.merge_all()

    with tf.Session() as sess:

        # 初始化变量
        sess.run(init)

        # 1_创建事件文件
        file_writer = tf.summary.FileWriter("./tmp/", graph=sess.graph)

        # 查看初始化模型参数之后的值
        print("训练前模型参数为：权重%f，偏置%f，损失为%f" % (weights.eval(), bias.eval(), error.eval()))
        # 开始训练
        for i in range(100):
            sess.run(optimizer)
            print("训练前模型参数为：权重%f，偏置%f，损失为%f" % (weights.eval(), bias.eval(), error.eval()))

            # 运行合并变量操作
            summary = sess.run(merged)
            # 将每次迭代后的变量写入事件文件
            file_writer.add_summary(summary, i)  # i是迭代次数

if __name__ == "__main__":
    linear_regression()

Tensorboard的可视化：http://ftl2018:6006/#graphs&run=.(火狐浏览器)

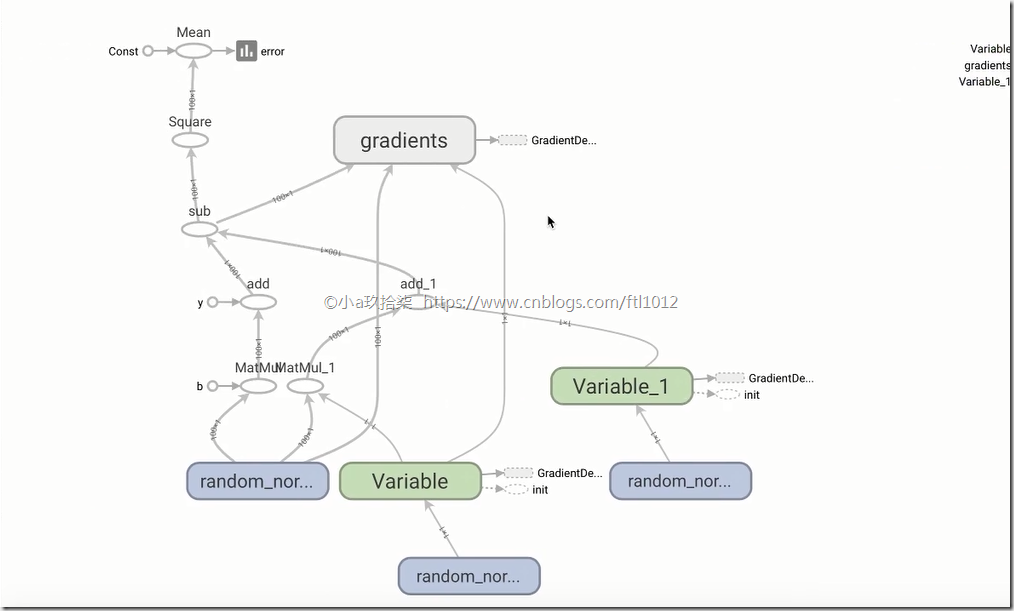
• 增加命名空间

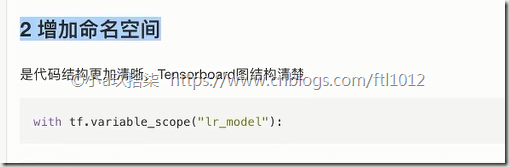
增加命名空间demo

import tensorflow as tf
import os

os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'

def linear_regression():
    """
    自实现一个线性回归
    :return:
    """
    # 第一步：
    # 1）准备数据
    with tf.variable_scope(name_or_scope='prepare_data'):
        X = tf.random_normal(shape=[100, 1], mean=2, name='feature')
        y_true = tf.matmul(X, [[0.8]]) + 0.7   # [[0.8]] 定义了一个一行一列

    # 2）构造模型
    # 定义模型参数 用 变量
    # trainable=False，的时候则后面的权重会不变，导致损失也不会变化太久，默认True
    with tf.variable_scope("create_model"):
        weights = tf.Variable(initial_value=tf.random_normal(shape=[1, 1]), trainable=True, name='weights')  # 随机产生一个一行一列
        bias = tf.Variable(initial_value=tf.random_normal(shape=[1, 1]), name='bias')   # 随机产生一个一行一列
        y_predict = tf.matmul(X, weights) + bias

    # 3）构造损失函数： 均方误差
    with tf.variable_scope("loss_function"):
        error = tf.reduce_mean(tf.square(y_predict - y_true))

    # 4）优化损失
    with tf.variable_scope("optimizer"):
        optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.01).minimize(error)

    # 显式地初始化变量
    init = tf.global_variables_initializer()

    # 第二步：收集变量
    tf.summary.scalar("error", error)
    tf.summary.histogram("weights", weights)
    tf.summary.histogram("bias", bias)

    # 第三步：合并变量
    merged = tf.summary.merge_all()

    with tf.Session() as sess:

        # 初始化变量
        sess.run(init)

        # 1_创建事件文件
        file_writer = tf.summary.FileWriter("./tmp/", graph=sess.graph)

        # 查看初始化模型参数之后的值
        print("训练前模型参数为：权重%f，偏置%f，损失为%f" % (weights.eval(), bias.eval(), error.eval()))
        # 开始训练
        for i in range(100):
            sess.run(optimizer)
            print("训练前模型参数为：权重%f，偏置%f，损失为%f" % (weights.eval(), bias.eval(), error.eval()))

            # 运行合并变量操作
            summary = sess.run(merged)
            # 将每次迭代后的变量写入事件文件
            file_writer.add_summary(summary, i)  # i是迭代次数

if __name__ == "__main__":
    linear_regression()

• 模型保存于加载

saver = tf.train.Saver(var_list=None,max_to_keep=5)
            1）实例化Saver
            2）保存
                saver.save(sess, path)
            3）加载
                saver.restore(sess, path)

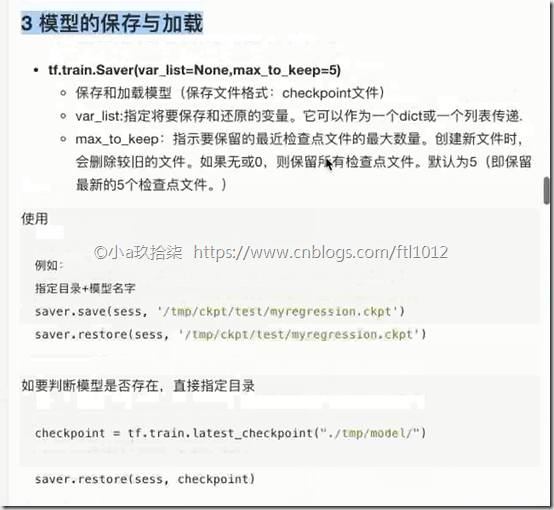
模型保存(需要提前准备好目录)与加载demo

import tensorflow as tf
import os

os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'

def linear_regression():
    """
    自实现一个线性回归
    :return:
    """
    # 第一步：
    # 1）准备数据
    with tf.variable_scope(name_or_scope='prepare_data'):
        X = tf.random_normal(shape=[100, 1], mean=2, name='feature')
        y_true = tf.matmul(X, [[0.8]]) + 0.7   # [[0.8]] 定义了一个一行一列

    # 2）构造模型
    # 定义模型参数 用 变量
    # trainable=False，的时候则后面的权重会不变，导致损失也不会变化太久，默认True
    with tf.variable_scope("create_model"):
        weights = tf.Variable(initial_value=tf.random_normal(shape=[1, 1]), trainable=True, name='weights')  # 随机产生一个一行一列
        bias = tf.Variable(initial_value=tf.random_normal(shape=[1, 1]), name='bias')   # 随机产生一个一行一列
        y_predict = tf.matmul(X, weights) + bias

    # 3）构造损失函数： 均方误差
    with tf.variable_scope("loss_function"):
        error = tf.reduce_mean(tf.square(y_predict - y_true))

    # 4）优化损失
    with tf.variable_scope("optimizer"):
        optimizer = tf.train.GradientDescentOptimizer(learning_rate=0.01).minimize(error)

    # 显式地初始化变量
    init = tf.global_variables_initializer()

    # 第二步：收集变量
    tf.summary.scalar("error", error)
    tf.summary.histogram("weights", weights)
    tf.summary.histogram("bias", bias)

    # 第三步：合并变量
    merged = tf.summary.merge_all()

    # 保存模型:创建Saver对象
    saver = tf.train.Saver(max_to_keep=5)

    with tf.Session() as sess:

        # 初始化变量
        sess.run(init)

        # 1_创建事件文件
        file_writer = tf.summary.FileWriter("./tmp/", graph=sess.graph)

        # 查看初始化模型参数之后的值
        print("训练前模型参数为：权重%f，偏置%f，损失为%f" % (weights.eval(), bias.eval(), error.eval()))
        # 开始训练
        for i in range(100):
            sess.run(optimizer)
            print("训练前模型参数为：权重%f，偏置%f，损失为%f" % (weights.eval(), bias.eval(), error.eval()))

            # 运行合并变量操作
            summary = sess.run(merged)
            # 将每次迭代后的变量写入事件文件
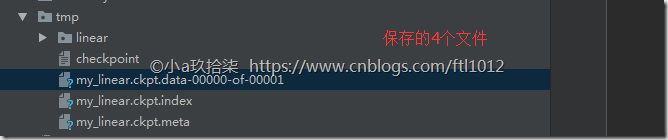
            file_writer.add_summary(summary, i)  # i是迭代次数

            # 保存模型(保存模型参数，而参数在会话中)--》路径需要先创建好
            if i % 10 == 0:
                saver.save(sess, "./tmp/my_linear.ckpt")
        # # 加载模型
        # if os.path.exists("./tmp/model/checkpoint"):
        #     saver.restore(sess, "./tmp/model/my_linear.ckpt")

if __name__ == "__main__":
    linear_regression()

• 命令行参数设置

命令行参数使用
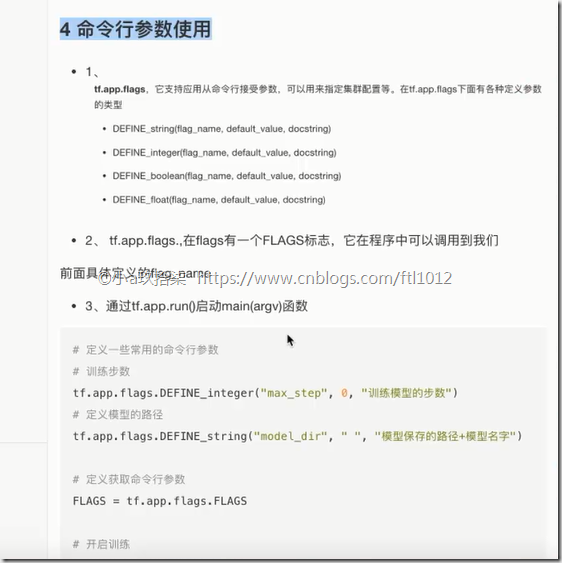
            1）tf.app.flags
                    tf.app.flags.DEFINE_integer("max_step", 0, "训练模型的步数")
                    tf.app.flags.DEFINE_string("model_dir", " ", "模型保存的路径+模型名字")
            2）FLAGS = tf.app.flags.FLAGS
                    通过FLAGS.max_step调用命令行中传过来的参数
            3、通过tf.app.run()启动main(argv)函数

具体调用：

命令行demo

import tensorflow as tf
import os

os.environ['TF_CPP_MIN_LOG_LEVEL'] = '2'

# 1）定义命令行参数
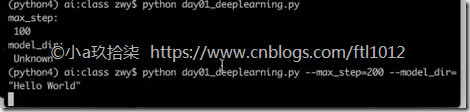
tf.app.flags.DEFINE_integer("max_step", 100, "训练模型的步数")
tf.app.flags.DEFINE_string("model_dir", "Unknown", "模型保存的路径+模型名字")

# 2）简化变量名
FLAGS = tf.app.flags.FLAGS

def command_demo():
    """
    命令行参数演示
    :return:
    """
    print("max_step:\n", FLAGS.max_step)
    print("model_dir:\n", FLAGS.model_dir)

    return None

def main(argv):
    print("code start", argv)
    return None

if __name__ == "__main__":
    # 命令行参数演示
    # command_demo()
    tf.app.run()