第六节,TensorFlow编程基础案例-保存和恢复模型(中)
在我们使用TensorFlow的时候,有时候需要训练一个比较复杂的网络,比如后面的AlexNet,ResNet,GoogleNet等等,由于训练这些网络花费的时间比较长,因此我们需要保存模型的参数。
编程基础案例中主要讲解模型的保存和恢复,以及使用几个案例使我们更好的理解这一块内容。
一 保存和载入模型
1.保存模型
首先需要建立一个saver,然后在session中通过saver的save即可将模型保存起来,代码如下:
'''
1.保存模型
''' '''
这里是各种构建模型graph的操作,省略.... '''
#创建saver对象
saver = tf.train.Saver()
with tf.Session() as sess:
#初始化张量
sess.run(tf.global_variables_initializer()) '''
这里是将数据喂入模型进行训练,省略... ''' #训练完成后,保存模型,如果file_name不存在,会自动创建
saver.save(sess,'save_path/file_name')
2.载入模型
载入模型只需要调用saver对象的restore()函数,会从指定的路径找到模型文件,并覆盖到相关参数中,代码如下:
'''
2.载入模型
'''
#创建saver对象
saver = tf.train.Saver()
with tf.Session() as sess:
#参数可以进行初始化,也可以不进行初始化,即使进行了初始化,初始化的值也会被restore的值覆盖掉
sess.run(tf.global_variables_initializer())
saver.restore(sess,'save_path/file_name')
二 保存/载入线性回归模型
在第四节我们讲了线性回归的案列,这里我们就保存这个案例的模型,然后恢复
'''
3.保存和恢复线性回归模型
'''
import numpy as np
import matplotlib.pyplot as plt
import os '''
一准备数据
''' #设定训练集数据长度
n_train = 100 #生成x数据,[-1,1]之间,均分成n_train个数据
train_x = np.linspace(-1,1,n_train).reshape(n_train,1) #把x乘以2,在加入(0,0.3)的高斯正太分布
train_y = 2*train_x + np.random.normal(loc=0.0,scale=0.3,size=[n_train,1]) #绘制x,y波形
plt.figure()
plt.plot(train_x,train_y,'ro',label='y=2x') #o使用圆点标记一个点
plt.legend()
plt.show() #重置图 (不清空该图的所有缓存)
tf.reset_default_graph() '''
二 搭建模型
''' '''
前向反馈
'''
#创建占位符
input_x = tf.placeholder(dtype=tf.float32)
input_y = tf.placeholder(dtype=tf.float32) #模型参数
w = tf.Variable(tf.truncated_normal(shape=[1],mean=0.0,stddev=1),name='w') #设置正太分布参数 初始化权重
b = tf.Variable(tf.truncated_normal(shape=[1],mean=0.0,stddev=1),name='b') #设置正太分布参数 初始化偏置 #前向结构
pred = tf.multiply(w,input_x) + b '''
反向传播bp
'''
#定义代价函数 选取二次代价函数
cost = tf.reduce_mean(tf.square(input_y - pred))
#设置求解器 采用梯度下降法 学习了设置为0.001
train = tf.train.GradientDescentOptimizer(learning_rate=0.001).minimize(cost) '''
三 迭代模型
'''
#设置迭代次数
training_epochs = 200
display_step = 20 #创建saver对象 在张量声明之后创建
saver = tf.train.Saver()
#生成模型的路径
savedir = './LinearRegression'
#模型文件
savefile = 'linearmodel.cpkt' #路径不存在创建目录
if not os.path.isdir(savedir):
os.mkdir(savedir) with tf.Session() as sess:
#初始化所有张量
sess.run(tf.global_variables_initializer()) #恢复模型
if os.path.isfile(os.path.join(savedir, savefile)+'.meta'):
saver.restore(sess,os.path.join(savedir,savefile)) #存放批次值和代价值
plotdata = {'batch_size':[],'loss':[]} #开始迭代
for epoch in range(training_epochs):
for (x,y) in zip(train_x,train_y):
#开始执行图
sess.run(train,feed_dict={input_x:x,input_y:y}) #一轮训练完成后 打印输出信息
if epoch % display_step == 0:
#计算代价值
loss = sess.run(cost,feed_dict={input_x:train_x,input_y:train_y})
print('Epoch {0} cost {1} w {2} b{3}'.format(epoch,loss,sess.run(w),sess.run(b))) #保存每display_step轮训练后的代价值以及当前迭代轮数
if not loss == np.nan:
plotdata['batch_size'].append(epoch)
plotdata['loss'].append(loss) #输出最终结果
print('Finished!')
print('cost {0} w {1} b {2}'.format(sess.run(cost,feed_dict={input_x:train_x,input_y:train_y}),sess.run(w),sess.run(b))) #预测
test_x = [2,4,5,7]
test_y = sess.run(pred,feed_dict={input_x:test_x})
print('prediction ',test_y) '''
四 可视化显示
'''
#绘制原数据点,和估计曲线
plt.figure(figsize=(4.2*2,3.2*1))
plt.subplot(121)
plt.plot(train_x,train_y,'ro',label='Original data')
plt.plot(train_x,sess.run(w)*train_x + sess.run(b),label ='Estimate data')
plt.legend() #绘制代价曲线
plt.subplot(122)
plt.plot(plotdata['batch_size'],plotdata['loss'],'b--')
plt.xlabel('batch_size')
plt.ylabel('loss')
plt.title('Minibatch run vs. Training loss')
plt.show() #保存参数
saver.save(sess,os.path.join(savedir, savefile))
我们可以看到在LinearRegression文件夹下面生成了四个文件:

这四个文件主要是:
- .meta(存储网络结构)、包含了这个TF图完整信息:如所有变量等。
- .data和.index(存储训练好的参数,也叫检查点文件)、这是一个二进制文件,包含所有权重,偏置,梯度和所有其他存储的变量的值。
- checkpoint(记录最新的模型)。保存最后的检查点的文件 ,如果同时保存了几个模型,则在这个文件还有这几个模型的变量数据,由于在这几个模型中可能存在同名变量,所以取得的数据可能有问题。所以解决方案是最后把不同模型保存在不同文件夹下,或者使用 tf.variable_scope指定变量名字分组。
我们运行多次这个代码,我们会发现我们每次都是在之前训练的基础上继续训练模型,这是因为每次训练我们都先恢复模型再继续训练。


三 分析模型内容
如何将我们保存的模型内容打印出来呢?这一节将教你如何将生成的模型的内容打印出来,并观察其存放的具体数据方式,同时显示如何将指定内容保存到模型文件中。
1.查看模型内容
'''
3.查看模型内容
'''
from tensorflow.python.tools.inspect_checkpoint import print_tensors_in_checkpoint_file
print_tensors_in_checkpoint_file(os.path.join(savedir,savefile),None,True)

tensor_name后面是创建的张量名称,接着是它的数值。
2.保存模型的其它方法
前面我们在创建saver对象的时候没有传入任何参数,实际上,tf.train.Saver()函数还可以传入参数来实现更高级的功能,可以指定存储张量名字与张量的对应关系,可以写成这样:
#或者指定保存参数 代表将张量w,b的值分别放到变量w和b名字中
saver = tf.train.Saver({'w':w,'b':b})
我们也可以这么写:
saver = tf.train.Saver([w,b]) #存放到一个list里面
savee = tf.train.Saver({v.opname:v for v in [w,b]}) #将op的name当做名字
下面展示一个例子:我们可以看到张量a的值被保存到张量名为b_param上,张量b的值保存到张量名为a_param上。
#给a和b分别指定一个固定的值,将它们颠倒文职存放
a = tf.Variable(1.0,name='a')
b = tf.Variable(2.0,name='b') #指定保存参数
saver = tf.train.Saver({'b_param':a,'a_param':b}) with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
#保存参数
saver.save(sess,'./test.cpkt') print_tensors_in_checkpoint_file('./test.cpkt',None,True)

注意:当我们在Saver()中指定了保存和恢复的变量时,在恢复的时候我们要保证模型文件中有该变量,不然会报错。保存的时候模型文件也只会保存指定的变量。如果我们想保存时除了恢复时指定的变量,还保存其他的所有变量,最好的解决方法是创建两个Saver()对象,一个用于恢复模型,一个用于保存模型。
四 检查点
由于我们在训练过程中可能会出现错误,如果我们在训练一个很大的网络的时候,训练到快结束的时候,突然报错,这样会导致我们之前的训练功亏一篑,我们心里可能就会很崩溃,因此最好的方法就是能够在训练的过程中也保存模型。TensorFlow就提供了一个这样的功能。
在训练中保存模型,我们习惯上称之为保存检查点(checkpoint)。
1.为模型添加保存检查点
为我们之前线性回归的案例追加'保存检查点'功能,通过该功能,可以生成检查点文件,并能够制定生成检查点文件的个数。
这个例子与保存模型的功能类似,只是保存的位置发生了变化,我们希望在显示信息是将检查点保存下来,因此需要在打印信息后面添加检查点。
另外在这里我们会用到Saver()类的另一个参数,max_to_keep = 1,表名最多保存一个检查点文件,这样在迭代过程中,新生成的模型就会覆盖以前的模型。
在保存时使用了如下代码传入了迭代次数:
#每隔display_step轮后保存一次检查点
saver.save(sess,os.path.join(savedir,savefile),global_step = epoch)
TensorFlow会将迭代次数一起放在检查点的文件上,所以在载入时,同样也要指定迭代次数。
# -*- coding: utf-8 -*-
"""
Created on Wed Apr 18 09:20:53 2018 @author: zy
""" '''
4.检查点(模型训练中保存模型)
''' '''
(1)为模型添加保存检查点(即训练中保存检查点)
''' import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
import os '''
一准备数据
''' #设定训练集数据长度
n_train = 100 #生成x数据,[-1,1]之间,均分成n_train个数据
train_x = np.linspace(-1,1,n_train).reshape(n_train,1) #把x乘以2,在加入(0,0.3)的高斯正太分布
train_y = 2*train_x + np.random.normal(loc=0.0,scale=0.3,size=[n_train,1]) #绘制x,y波形
plt.figure()
plt.plot(train_x,train_y,'ro',label='y=2x') #o使用圆点标记一个点
plt.legend()
plt.show() tf.reset_default_graph() '''
二 搭建模型
''' '''
前向反馈
'''
#创建占位符
input_x = tf.placeholder(dtype=tf.float32)
input_y = tf.placeholder(dtype=tf.float32) #模型参数
w = tf.Variable(tf.truncated_normal(shape=[1],mean=0.0,stddev=1),name='w') #设置正太分布参数 初始化权重
b = tf.Variable(tf.truncated_normal(shape=[1],mean=0.0,stddev=1),name='b') #设置正太分布参数 初始化偏置 #前向结构
pred = tf.multiply(w,input_x) + b '''
反向传播bp
'''
#定义代价函数 选取二次代价函数
cost = tf.reduce_mean(tf.square(input_y - pred))
#设置求解器 采用梯度下降法 学习了设置为0.001
train = tf.train.GradientDescentOptimizer(learning_rate=0.001).minimize(cost) '''
三 迭代模型
'''
#设置迭代次数
training_epochs = 200
display_step = 20 #生成Saver对象
saver = tf.train.Saver(max_to_keep = 1) #生成模型的路径
savedir = './LinearRegression'
#模型文件
savefile = 'linearmodel.cpkt' #路径不存在创建目录
if not os.path.isdir(savedir):
os.mkdir(savedir) with tf.Session() as sess:
#初始化所有张量
sess.run(tf.global_variables_initializer()) #恢复模型
if os.path.isfile(os.path.join(savedir, savefile)+'.meta'):
saver.restore(sess,os.path.join(savedir,savefile)) #存放批次值和代价值
plotdata = {'batch_size':[],'loss':[]} #开始迭代
for epoch in range(training_epochs):
for (x,y) in zip(train_x,train_y):
#开始执行图
sess.run(train,feed_dict={input_x:x,input_y:y}) #一轮训练完成后 打印输出信息
if epoch % display_step == 0:
#计算代价值
loss = sess.run(cost,feed_dict={input_x:train_x,input_y:train_y})
print('Epoch {0} cost {1} w {2} b{3}'.format(epoch,loss,sess.run(w),sess.run(b))) #保存每display_step轮训练后的代价值以及当前迭代轮数
if not loss == np.nan:
plotdata['batch_size'].append(epoch)
plotdata['loss'].append(loss) #每隔display_step轮后保存一次检查点
saver.save(sess,os.path.join(savedir,savefile),global_step = epoch) #输出最终结果
print('Finished!')
print('cost {0} w {1} b {2}'.format(sess.run(cost,feed_dict={input_x:train_x,input_y:train_y}),sess.run(w),sess.run(b))) #预测
test_x = [2,4,5,7]
test_y = sess.run(pred,feed_dict={input_x:test_x})
print('prediction ',test_y) '''
四 可视化显示
'''
#绘制原数据点,和估计曲线
plt.figure(figsize=(4.2*2,3.2*1))
plt.subplot(121)
plt.plot(train_x,train_y,'ro',label='Original data')
plt.plot(train_x,sess.run(w)*train_x + sess.run(b),label ='Estimate data')
plt.legend() #绘制代价曲线
plt.subplot(122)
plt.plot(plotdata['batch_size'],plotdata['loss'],'b--')
plt.xlabel('batch_size')
plt.ylabel('loss')
plt.title('Minibatch run vs. Training loss')
plt.show() #重启一个session,载入检查点 方法一
load_epoch = 180
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
saver.restore(sess,os.path.join(savedir,savefile+'-'+str(load_epoch)))
test_x = [2,4,5,7]
test_y = sess.run(pred,feed_dict={input_x:test_x})
print('prediction ',test_y)
运行完后,我们会看到多了几个文件,多的那几个文件就是检查点文件:这里有必要说一下180怎么来的,180就是我们最后一次保存检查点的迭代次数
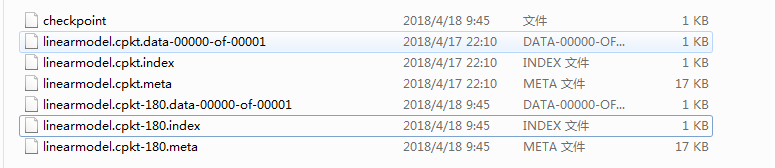
在载入模型时,我们每次都要指定迭代次数,因此会比较麻烦,这里有几种种方法,直接载入最近保存的检查点文件,个人推荐第三种代码如下:、
'''
由于恢复模型,需要指定迭代次数,比较麻烦,我们可以直接载入最近保存的检查点文件 方法二
'''
with tf.Session() as sess:
#需要指定检查点文件所在目录
ckpt = tf.train.get_checkpoint_state(savedir)
if ckpt and ckpt.model_checkpoint_path:
saver.restore(sess,ckpt.model_checkpoint_path) '''
或者 方法三
'''
with tf.Session() as sess:
ckpt = tf.train.latest_checkpoint(savedir)
if ckpt != None:
#恢复模型
saver.restore(sess,ckpt)
#使用默认图,即我们定义的线性回归模型 并获取模型中的tensor
graph = tf.get_default_graph()
weight = graph.get_tensor_by_name('w:0')
bias = graph.get_tensor_by_name('b:0') print(sess.run([w,b])) #在加载的模型后继续加载新的网络层
add_on_op = tf.multiply(w,2)
print(sess.run(add_on_op)) '''
或者 直接把网络结构加载进来(.meta),不可以重写网络结构,不然会出现变量重命名冲突问题。 方法四
'''
#清空默认图的内容
tf.reset_default_graph()
with tf.Session() as sess:
#加载以前保存的网络 将保存在.meta文件中的图添加到当前的图中
new_saver = tf.train.import_meta_graph(os.path.join(savedir,savefile)+'.meta')
#从指定目录下获取最近一次检查点
new_saver.restore(sess,tf.train.latest_checkpoint(savedir)) #使用加载的模型 并获取模型中的tensor
graph = tf.get_default_graph()
weight = graph.get_tensor_by_name('w:0')
bias = graph.get_tensor_by_name('b:0') print(sess.run([weight,bias])) #在加载的模型后继续加载新的网络层
add_on_op = tf.multiply(weight,2)
print(sess.run(add_on_op))
运行结果如下:

这里有几点需要注意:上面介绍了四种类恢复模型的方法,前三种类似,可以概括为一类,最后一种比较特殊:
- 第一种是saver.restore(sess, 'aaaa.ckpt')类型的,这种方法的本质是读取全部参数,并加载到已经定义好的网络结构上,因此相当于给网络的weights和biases赋值并执行tf.global_variables_initializer()。这种方法的缺点是使用前必须重写网络结构,而且网络结构要和保存的参数完全对上。
- 第二种就比较高端,直接把网络结构加载进来(.meta),不可以重写网络结构,不然会出现变量重命名冲突问题。
2.更简便地保存检查点
这里介绍使用tf.train.MonitoredTrainingSession函数来保存检查点,该函数可以直接实现保存和载入检查点模型的文件。与上一个案例不同的是,这里并不是按照循环步数来保存,而是按照训练时间来保存,通过指定save_checkpoint_secs参数的具体秒数,来设置每训练多久保存一次检查点。
'''
(2) 使用tf.train.MonitoredTrainingSession按时间来保存检查点
'''
#清空默认图的内容
tf.reset_default_graph()
#设置检查点路径
savedir = './LinearRegression/checkpoints'
global_step = tf.train.get_or_create_global_step()
#通过向 "ref" 添加 "value" 来更新 "ref"。此操作在更新完成后输出 "ref"。
step = tf.assign_add(global_step,1)
with tf.train.MonitoredTrainingSession(checkpoint_dir = savedir,save_checkpoint_secs = 2) as sess:
print(sess.run([global_step]))
#启用死循环,当sess不结束时就不停止
while not sess.should_stop():
#运行自加1操作
i =sess.run(step)
print(i)
巡行结果如下:
并且在检查点路径下生成如下文件:
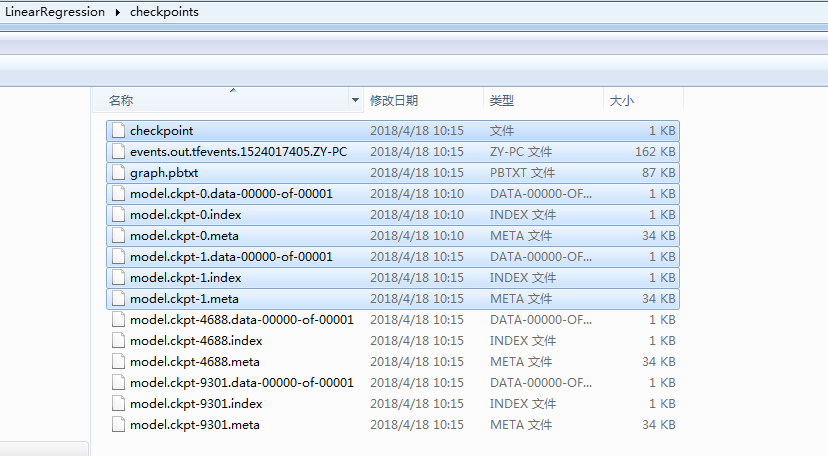
在使用该方法有两点需要注意:
- save_checkpoint_secs参数默认时间是10分钟。
- 使用该方法,必须定义global_step变量,否则会报错。
注意:程序中如果有定义检查点文件的保存路径savedir,则该路径必须是相对路径,且以./开头,比如./data,不然运行时加载模型可能会出错。
完整代码:
# -*- coding: utf-8 -*-
"""
Created on Tue Apr 17 20:56:00 2018 @author: zy
""" import tensorflow as tf
'''
TensorFlow 编程基础上
这一节主要讲解模型的保存和恢复,以及使用几个案例使我们更好的理解这一块内容。
''' '''
1.保存模型
''' '''
这里是各种构建模型graph的操作,省略.... '''
#创建saver对象
saver = tf.train.Saver()
with tf.Session() as sess:
#初始化张量
sess.run(tf.global_variables_initializer()) '''
这里是将数据喂如模型进行训练,省略... ''' #训练完成后,保存模型,如果file_name不存在,会自动创建
saver.save(sess,'save_path/file_name') '''
2.载入模型
'''
#创建saver对象
saver = tf.train.Saver()
with tf.Session() as sess:
#参数可以进行初始化,也可以不进行初始化,即使进行了初始化,初始化的值也会被restore的值覆盖掉
sess.run(tf.global_variables_initializer())
saver.restore(sess,'save_path/file_name') '''
3.保存和恢复线性回归模型
'''
import numpy as np
import matplotlib.pyplot as plt
import os '''
一准备数据
''' #设定训练集数据长度
n_train = 100 #生成x数据,[-1,1]之间,均分成n_train个数据
train_x = np.linspace(-1,1,n_train).reshape(n_train,1) #把x乘以2,在加入(0,0.3)的高斯正太分布
train_y = 2*train_x + np.random.normal(loc=0.0,scale=0.3,size=[n_train,1]) #绘制x,y波形
plt.figure()
plt.plot(train_x,train_y,'ro',label='y=2x') #o使用圆点标记一个点
plt.legend()
plt.show() #重置图
tf.reset_default_graph() '''
二 搭建模型
''' '''
前向反馈
'''
#创建占位符
input_x = tf.placeholder(dtype=tf.float32)
input_y = tf.placeholder(dtype=tf.float32) #模型参数
w = tf.Variable(tf.truncated_normal(shape=[1],mean=0.0,stddev=1),name='w') #设置正太分布参数 初始化权重
b = tf.Variable(tf.truncated_normal(shape=[1],mean=0.0,stddev=1),name='b') #设置正太分布参数 初始化偏置 #前向结构
pred = tf.multiply(w,input_x) + b '''
反向传播bp
'''
#定义代价函数 选取二次代价函数
cost = tf.reduce_mean(tf.square(input_y - pred))
#设置求解器 采用梯度下降法 学习了设置为0.001
train = tf.train.GradientDescentOptimizer(learning_rate=0.001).minimize(cost) '''
三 迭代模型
'''
#设置迭代次数
training_epochs = 200
display_step = 20 #创建saver对象 在张量声明之后创建
#saver = tf.train.Saver() #或者指定保存参数 代表将张量w,b的值分别放到变量w和b名字中
saver = tf.train.Saver({'w':w,'b':b})
#或者写成
#saver = tf.train.Saver([w,b]) #存放到一个list里面
#savee = tf.train.Saver({v.opname:v for v in [w,b]}) #将op的name当做名字 #生成模型的路径
savedir = './LinearRegression'
#模型文件
savefile = 'linearmodel.cpkt' #路径不存在创建目录
if not os.path.isdir(savedir):
os.mkdir(savedir) with tf.Session() as sess:
#初始化所有张量
sess.run(tf.global_variables_initializer()) #恢复模型
if os.path.isfile(os.path.join(savedir, savefile)+'.meta'):
saver.restore(sess,os.path.join(savedir,savefile)) #存放批次值和代价值
plotdata = {'batch_size':[],'loss':[]} #开始迭代
for epoch in range(training_epochs):
for (x,y) in zip(train_x,train_y):
#开始执行图
sess.run(train,feed_dict={input_x:x,input_y:y}) #一轮训练完成后 打印输出信息
if epoch % display_step == 0:
#计算代价值
loss = sess.run(cost,feed_dict={input_x:train_x,input_y:train_y})
print('Epoch {0} cost {1} w {2} b{3}'.format(epoch,loss,sess.run(w),sess.run(b))) #保存每display_step轮训练后的代价值以及当前迭代轮数
if not loss == np.nan:
plotdata['batch_size'].append(epoch)
plotdata['loss'].append(loss) #输出最终结果
print('Finished!')
print('cost {0} w {1} b {2}'.format(sess.run(cost,feed_dict={input_x:train_x,input_y:train_y}),sess.run(w),sess.run(b))) #预测
test_x = [2,4,5,7]
test_y = sess.run(pred,feed_dict={input_x:test_x})
print('prediction ',test_y) '''
四 可视化显示
'''
#绘制原数据点,和估计曲线
plt.figure(figsize=(4.2*2,3.2*1))
plt.subplot(121)
plt.plot(train_x,train_y,'ro',label='Original data')
plt.plot(train_x,sess.run(w)*train_x + sess.run(b),label ='Estimate data')
plt.legend() #绘制代价曲线
plt.subplot(122)
plt.plot(plotdata['batch_size'],plotdata['loss'],'b--')
plt.xlabel('batch_size')
plt.ylabel('loss')
plt.title('Minibatch run vs. Training loss')
plt.show() #保存参数
saver.save(sess,os.path.join(savedir, savefile)) '''
3.查看模型内容
'''
from tensorflow.python.tools.inspect_checkpoint import print_tensors_in_checkpoint_file
print_tensors_in_checkpoint_file(os.path.join(savedir,savefile),None,True) #给a和b分别指定一个固定的值,将它们颠倒文职存放
a = tf.Variable(1.0,name='a')
b = tf.Variable(2.0,name='b') #指定保存参数
saver = tf.train.Saver({'b_param':a,'a_param':b}) with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
#保存参数
saver.save(sess,'./test.cpkt') print_tensors_in_checkpoint_file('./test.cpkt',None,True)
# -*- coding: utf-8 -*-
"""
Created on Wed Apr 18 09:20:53 2018 @author: zy
""" '''
4.检查点的适用(模型训练中保存模型)
''' '''
(1)为模型添加保存检查点(即训练中保存检查点)
''' import tensorflow as tf
import numpy as np
import matplotlib.pyplot as plt
import os '''
一准备数据
''' #设定训练集数据长度
n_train = 100 #生成x数据,[-1,1]之间,均分成n_train个数据
train_x = np.linspace(-1,1,n_train).reshape(n_train,1) #把x乘以2,在加入(0,0.3)的高斯正太分布
train_y = 2*train_x + np.random.normal(loc=0.0,scale=0.3,size=[n_train,1]) #绘制x,y波形
plt.figure()
plt.plot(train_x,train_y,'ro',label='y=2x') #o使用圆点标记一个点
plt.legend()
plt.show() tf.reset_default_graph() '''
二 搭建模型
''' '''
前向反馈
'''
#创建占位符
input_x = tf.placeholder(dtype=tf.float32)
input_y = tf.placeholder(dtype=tf.float32) #模型参数
w = tf.Variable(tf.truncated_normal(shape=[1],mean=0.0,stddev=1),name='w') #设置正太分布参数 初始化权重
b = tf.Variable(tf.truncated_normal(shape=[1],mean=0.0,stddev=1),name='b') #设置正太分布参数 初始化偏置 #前向结构
pred = tf.multiply(w,input_x) + b '''
反向传播bp
'''
#定义代价函数 选取二次代价函数
cost = tf.reduce_mean(tf.square(input_y - pred))
#设置求解器 采用梯度下降法 学习了设置为0.001
train = tf.train.GradientDescentOptimizer(learning_rate=0.001).minimize(cost) '''
三 迭代模型
'''
#设置迭代次数
training_epochs = 200
display_step = 20 #生成Saver对象
saver = tf.train.Saver(max_to_keep = 1) #生成模型的路径
savedir = './LinearRegression'
#模型文件
savefile = 'linearmodel.cpkt' #路径不存在创建目录
if not os.path.isdir(savedir):
os.mkdir(savedir) with tf.Session() as sess:
#初始化所有张量
sess.run(tf.global_variables_initializer()) #恢复模型
if os.path.isfile(os.path.join(savedir, savefile)+'.meta'):
saver.restore(sess,os.path.join(savedir,savefile)) #存放批次值和代价值
plotdata = {'batch_size':[],'loss':[]} #开始迭代
for epoch in range(training_epochs):
for (x,y) in zip(train_x,train_y):
#开始执行图
sess.run(train,feed_dict={input_x:x,input_y:y}) #一轮训练完成后 打印输出信息
if epoch % display_step == 0:
#计算代价值
loss = sess.run(cost,feed_dict={input_x:train_x,input_y:train_y})
print('Epoch {0} cost {1} w {2} b{3}'.format(epoch,loss,sess.run(w),sess.run(b))) #保存每display_step轮训练后的代价值以及当前迭代轮数
if not loss == np.nan:
plotdata['batch_size'].append(epoch)
plotdata['loss'].append(loss) #每隔display_step轮后保存一次检查点
saver.save(sess,os.path.join(savedir,savefile),global_step = epoch) #输出最终结果
print('Finished!')
print('cost {0} w {1} b {2}'.format(sess.run(cost,feed_dict={input_x:train_x,input_y:train_y}),sess.run(w),sess.run(b))) #预测
test_x = [2,4,5,7]
test_y = sess.run(pred,feed_dict={input_x:test_x})
print('prediction ',test_y) '''
四 可视化显示
'''
#绘制原数据点,和估计曲线
plt.figure(figsize=(4.2*2,3.2*1))
plt.subplot(121)
plt.plot(train_x,train_y,'ro',label='Original data')
plt.plot(train_x,sess.run(w)*train_x + sess.run(b),label ='Estimate data')
plt.legend() #绘制代价曲线
plt.subplot(122)
plt.plot(plotdata['batch_size'],plotdata['loss'],'b--')
plt.xlabel('batch_size')
plt.ylabel('loss')
plt.title('Minibatch run vs. Training loss')
plt.show() '''
重启一个session,载入检查点 方法一
'''
load_epoch = 180
with tf.Session() as sess:
sess.run(tf.global_variables_initializer())
saver.restore(sess,os.path.join(savedir,savefile+'-'+str(load_epoch)))
test_x = [2,4,5,7]
test_y = sess.run(pred,feed_dict={input_x:test_x})
print('prediction ',test_y) '''
由于恢复模型,需要指定迭代次数,比较麻烦,我们可以直接载入最近保存的检查点文件 方法二
'''
with tf.Session() as sess:
#需要指定检查点文件所在目录
ckpt = tf.train.get_checkpoint_state(savedir)
if ckpt and ckpt.model_checkpoint_path:
saver.restore(sess,ckpt.model_checkpoint_path) '''
或者 方法三
'''
with tf.Session() as sess:
ckpt = tf.train.latest_checkpoint(savedir)
if ckpt != None:
#恢复模型
saver.restore(sess,ckpt)
#使用默认图,即我们定义的线性回归模型 并获取模型中的tensor
graph = tf.get_default_graph()
weight = graph.get_tensor_by_name('w:0')
bias = graph.get_tensor_by_name('b:0') print(sess.run([w,b])) #在加载的模型后继续加载新的网络层
add_on_op = tf.multiply(w,2)
print(sess.run(add_on_op)) '''
或者 直接把网络结构加载进来(.meta),不可以重写网络结构,不然会出现变量重命名冲突问题。 方法四
'''
#清空默认图的内容
tf.reset_default_graph()
with tf.Session() as sess:
#加载以前保存的网络 将保存在.meta文件中的图添加到当前的图中
new_saver = tf.train.import_meta_graph(os.path.join(savedir,savefile)+'.meta')
#从指定目录下获取最近一次检查点
new_saver.restore(sess,tf.train.latest_checkpoint(savedir)) #使用加载的模型 并获取模型中的tensor
graph = tf.get_default_graph()
weight = graph.get_tensor_by_name('w:0')
bias = graph.get_tensor_by_name('b:0') print(sess.run([weight,bias])) #在加载的模型后继续加载新的网络层
add_on_op = tf.multiply(weight,2)
print(sess.run(add_on_op)) '''
(2) 使用tf.train.MonitoredTrainingSession按时间来保存检查点
'''
#清空默认图的内容
tf.reset_default_graph()
#设置检查点路径
savedir = './LinearRegression/checkpoints'
global_step = tf.train.get_or_create_global_step()
#通过向 "ref" 添加 "value" 来更新 "ref"。此操作在更新完成后输出 "ref"。
step = tf.assign_add(global_step,1)
with tf.train.MonitoredTrainingSession(checkpoint_dir = savedir,save_checkpoint_secs = 2) as sess:
print(sess.run([global_step]))
#启用死循环,当sess不结束时就不停止
while not sess.should_stop():
#运行自加1操作
i =sess.run(step)
print(i)
第六节,TensorFlow编程基础案例-保存和恢复模型(中)的更多相关文章
- 第五节,TensorFlow编程基础案例-session使用(上)
在第一节中我们已经介绍了一些TensorFlow的编程技巧;第一节,TensorFlow基本用法,但是内容过于偏少,对于TensorFlow的讲解并不多,这一节对之前的内容进行补充,并更加深入了解讲解 ...
- AI - TensorFlow - 示例05:保存和恢复模型
保存和恢复模型(Save and restore models) 官网示例:https://www.tensorflow.org/tutorials/keras/save_and_restore_mo ...
- 第七节,TensorFlow编程基础案例-TensorBoard以及常用函数、共享变量、图操作(下)
这一节主要来介绍TesorFlow的可视化工具TensorBoard,以及TensorFlow基础类型定义.函数操作,后面又介绍到了共享变量和图操作. 一 TesnorBoard可视化操作 Tenso ...
- TensorFlow学习笔记:保存和读取模型
TensorFlow 更新频率实在太快,从 1.0 版本正式发布后,很多 API 接口就发生了改变.今天用 TF 训练了一个 CNN 模型,结果在保存模型的时候居然遇到各种问题.Google 搜出来的 ...
- 第4节:Java基础 - 必知必会(中)
第4节:Java基础 - 必知必会(中) 本小节是Java基础篇章的第二小节,主要讲述抽象类与接口的区别,注解以及反射等知识点. 一.抽象类和接口有什么区别 抽象类和接口的主要区别可以总结如下: 抽象 ...
- TensorFlow——tensorflow编程基础
0.tensorflow中的模型运行基础 tensorflow的运行机制属于定义和运行相分离,在操作层面可以抽象成两种:模型构建和模型运行. 在模型构建中的常见概念: 张量(tensor):数据,即某 ...
- 1 如何使用pb文件保存和恢复模型进行迁移学习(学习Tensorflow 实战google深度学习框架)
学习过程是Tensorflow 实战google深度学习框架一书的第六章的迁移学习环节. 具体见我提出的问题:https://www.tensorflowers.cn/t/5314 参考https:/ ...
- Tensorflow编程基础之Mnist手写识别实验+关于cross_entropy的理解
好久没有静下心来写点东西了,最近好像又回到了高中时候的状态,休息不好,无法全心学习,恶性循环,现在终于调整的好一点了,听着纯音乐突然非常伤感,那些曾经快乐的大学时光啊,突然又慢慢的一下子出现在了眼前, ...
- 那些年被我坑过的Python——玄而又玄(第六章 面向对象编程基础)
面向对象编程: 面向对象顾名思义,就是把组织代码的粒度从函数级别抽象到对象级别,对象是通过类来生成的,类可以想象为模板或进本框架而对象是在原有模板或框架的基础上增加详细信息的实体,类,有分类.聚类的含 ...
随机推荐
- Java的hashCode和equals方法
当然健壮的代码,两个都重写那是最好. 用不到hashCode的, 也没有必要重写hashCode. 个人感觉. 哈希机制的Java集合类,例如 Hashtable, HashMap, HashSet ...
- AVL树,红黑树
AVL树 https://baike.baidu.com/item/AVL%E6%A0%91/10986648 在计算机科学中,AVL树是最先发明的自平衡二叉查找树.在AVL树中任何节点的两个子树的高 ...
- QTP 自动货测试桌面程序-笔记(添加控件仓库并关联到action)
录制或编写脚本前先添加行为对应的控件仓库: 心得:多个测试action使用的同一个窗体的仓库单独放于一个仓库中,可以在多个action中添加关联使用 将同一个窗体的控件只放于一个仓库中,减少使用时的名 ...
- css元素选择器
css的元素选择器就是html的标签名:
- vue 关于生命周期
序言: 1. vue 单组件的生命周期: 2. vue 父子组件的生命周期: 3. axios 异步请求 与 vue 的组件周期: 一.vue 每个组件的生命周期 关于每个组件的生命周期,官方文档里也 ...
- mpi4python
转载:https://zhuanlan.zhihu.com/p/25332041 前言 在高性能计算的项目中我们通常都会使用效率更高的编译型的语言例如C.C++.Fortran等,但是由于Python ...
- codeforces433B
Kuriyama Mirai's Stones CodeForces - 433B 有n颗宝石,每个宝石都有自己的价值. 然后m次询问.问区间[i,j]的宝石的总值,或者问排序后的区间[i,j]的总值 ...
- python 机械学习之sklearn的数据正规化
from sklearn import preprocessing #导入sklearn的处理函数用于处理一些大值数据 x_train, x_test, y_train, y_test = tr ...
- DRF 分页组件
Django Rest Framework 分页组件 DRF的分页 为什么要使用分页 其实这个不说大家都知道,大家写项目的时候也是一定会用的, 我们数据库有几千万条数据,这些数据需要展示,我们不可能直 ...
- HTML协议
一,HTML协议 简介 超文本传输协议(英文:HyperText Transfer Protocol,缩写:HTTP)是一种用于分布式.协作式和超媒体信息系统的应用层协议.HTTP是万维网的数据通信的 ...
