Codeforces Round #404 (Div. 2) A,B,C,D,E 暴力，暴力，二分，范德蒙恒等式，树状数组+分块

题目链接：http://codeforces.com/contest/785

A. Anton and Polyhedrons

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Anton's favourite geometric figures are regular polyhedrons. Note that there are five kinds of regular polyhedrons:

• Tetrahedron. Tetrahedron has 4 triangular faces.
• Cube. Cube has 6 square faces.
• Octahedron. Octahedron has 8 triangular faces.
• Dodecahedron. Dodecahedron has 12 pentagonal faces.
• Icosahedron. Icosahedron has 20 triangular faces.

All five kinds of polyhedrons are shown on the picture below:

Anton has a collection of n polyhedrons. One day he decided to know, how many faces his polyhedrons have in total. Help Anton and find this number!

Input

The first line of the input contains a single integer n (1 ≤ n ≤ 200 000) — the number of polyhedrons in Anton's collection.

Each of the following n lines of the input contains a string si — the name of the i-th polyhedron in Anton's collection. The string can look like this:

• "Tetrahedron" (without quotes), if the i-th polyhedron in Anton's collection is a tetrahedron.
• "Cube" (without quotes), if the i-th polyhedron in Anton's collection is a cube.
• "Octahedron" (without quotes), if the i-th polyhedron in Anton's collection is an octahedron.
• "Dodecahedron" (without quotes), if the i-th polyhedron in Anton's collection is a dodecahedron.
• "Icosahedron" (without quotes), if the i-th polyhedron in Anton's collection is an icosahedron.

Output

Output one number — the total number of faces in all the polyhedrons in Anton's collection.

Examples

input

4
Icosahedron
Cube
Tetrahedron
Dodecahedron

output

42

input

3
Dodecahedron
Octahedron
Octahedron

output

28

Note

In the first sample Anton has one icosahedron, one cube, one tetrahedron and one dodecahedron. Icosahedron has 20 faces, cube has 6 faces, tetrahedron has 4 faces and dodecahedron has 12 faces. In total, they have 20 + 6 + 4 + 12 = 42 faces.

按题意模拟即可；

#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<iostream>
#include<cstdio>
#include<cmath>
#include<string>
#include<queue>
#include<algorithm>
#include<stack>
#include<cstring>
#include<vector>
#include<list>
#include<set>
#include<map>
using namespace std;
#define ll long long
#define pi (4*atan(1.0))
#define eps 1e-14
#define bug(x)  cout<<"bug"<<x<<endl;
const int N=2e3+,M=1e6+,inf=1e9+;
const ll INF=1e17;
char a[N];
int main()
{
    int n;
    int ans=;
    scanf("%d",&n);
    for(int i=;i<=n;i++)
    {
        scanf("%s",&a);
        if(a[]=='T')
            ans+=;
        else if(a[]=='C')
            ans+=;
        else if(a[]=='O')
            ans+=;
        else if(a[]=='D')
            ans+=;
        else
            ans+=;
    }
    cout<<ans<<endl;
    return ;
}

B. Anton and Classes

time limit per test

4 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

Anton likes to play chess. Also he likes to do programming. No wonder that he decided to attend chess classes and programming classes.

Anton has n variants when he will attend chess classes, i-th variant is given by a period of time (l1, i, r1, i). Also he has m variants when he will attend programming classes, i-th variant is given by a period of time (l2, i, r2, i).

Anton needs to choose exactly one of n possible periods of time when he will attend chess classes and exactly one of m possible periods of time when he will attend programming classes. He wants to have a rest between classes, so from all the possible pairs of the periods he wants to choose the one where the distance between the periods is maximal.

The distance between periods (l1, r1) and (l2, r2) is the minimal possible distance between a point in the first period and a point in the second period, that is the minimal possible |i - j|, where l1 ≤ i ≤ r1 and l2 ≤ j ≤ r2. In particular, when the periods intersect, the distance between them is 0.

Anton wants to know how much time his rest between the classes will last in the best case. Help Anton and find this number!

Input

The first line of the input contains a single integer n (1 ≤ n ≤ 200 000) — the number of time periods when Anton can attend chess classes.

Each of the following n lines of the input contains two integers l1, i and r1, i (1 ≤ l1, i ≤ r1, i ≤ 109) — the i-th variant of a period of time when Anton can attend chess classes.

The following line of the input contains a single integer m (1 ≤ m ≤ 200 000) — the number of time periods when Anton can attend programming classes.

Each of the following m lines of the input contains two integers l2, i and r2, i (1 ≤ l2, i ≤ r2, i ≤ 109) — the i-th variant of a period of time when Anton can attend programming classes.

Output

Output one integer — the maximal possible distance between time periods.

Examples

input

3
1 5
2 6
2 3
2
2 4
6 8

output

3

input

3
1 5
2 6
3 7
2
2 4
1 4

output

0

Note

In the first sample Anton can attend chess classes in the period (2, 3) and attend programming classes in the period (6, 8). It's not hard to see that in this case the distance between the periods will be equal to 3.

In the second sample if he chooses any pair of periods, they will intersect. So the answer is 0.

找两个区间相差最远；

来回扫一遍即可；

#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<iostream>
#include<cstdio>
#include<cmath>
#include<string>
#include<queue>
#include<algorithm>
#include<stack>
#include<cstring>
#include<vector>
#include<list>
#include<set>
#include<map>
using namespace std;
#define ll long long
#define pi (4*atan(1.0))
#define eps 1e-14
#define bug(x)  cout<<"bug"<<x<<endl;
const int N=2e3+,M=1e6+,inf=1e9+;
const ll INF=1e17;
char a[N];
int main()
{
    int n,m;
    scanf("%d",&n);
    int minn1=inf;
    int maxx2=;
    for(int i=;i<=n;i++)
    {
        int x,y;
        scanf("%d%d",&x,&y);
        minn1=min(minn1,y);
        maxx2=max(maxx2,x);
    }
    scanf("%d",&m);
    int maxx1=;
    int minn2=inf;
    for(int i=;i<=m;i++)
    {
        int x,y;
        scanf("%d%d",&x,&y);
        maxx1=max(maxx1,x);
        minn2=min(minn2,y);
    }
    cout<<max(max(,maxx2-minn2),maxx1-minn1)<<endl;
    return ;
}

C. Anton and Fairy Tale

time limit per test

1 second

memory limit per test

256 megabytes

input

standard input

output

standard output

Anton likes to listen to fairy tales, especially when Danik, Anton's best friend, tells them. Right now Danik tells Anton a fairy tale:

"Once upon a time, there lived an emperor. He was very rich and had much grain. One day he ordered to build a huge barn to put there all his grain. Best builders were building that barn for three days and three nights. But they overlooked and there remained a little hole in the barn, from which every day sparrows came through. Here flew a sparrow, took a grain and flew away..."

More formally, the following takes place in the fairy tale. At the beginning of the first day the barn with the capacity of n grains was full. Then, every day (starting with the first day) the following happens:

• m grains are brought to the barn. If m grains doesn't fit to the barn, the barn becomes full and the grains that doesn't fit are brought back (in this problem we can assume that the grains that doesn't fit to the barn are not taken into account).
• Sparrows come and eat grain. In the i-th day i sparrows come, that is on the first day one sparrow come, on the second day two sparrows come and so on. Every sparrow eats one grain. If the barn is empty, a sparrow eats nothing.

Anton is tired of listening how Danik describes every sparrow that eats grain from the barn. Anton doesn't know when the fairy tale ends, so he asked you to determine, by the end of which day the barn will become empty for the first time. Help Anton and write a program that will determine the number of that day!

Input

The only line of the input contains two integers n and m (1 ≤ n, m ≤ 1018) — the capacity of the barn and the number of grains that are brought every day.

Output

Output one integer — the number of the day when the barn will become empty for the first time. Days are numbered starting with one.

Examples

input

5 2

output

4

input

8 1

output

5

Note

In the first sample the capacity of the barn is five grains and two grains are brought every day. The following happens:

• At the beginning of the first day grain is brought to the barn. It's full, so nothing happens.
• At the end of the first day one sparrow comes and eats one grain, so 5 - 1 = 4 grains remain.
• At the beginning of the second day two grains are brought. The barn becomes full and one grain doesn't fit to it.
• At the end of the second day two sparrows come. 5 - 2 = 3 grains remain.
• At the beginning of the third day two grains are brought. The barn becomes full again.
• At the end of the third day three sparrows come and eat grain. 5 - 3 = 2 grains remain.
• At the beginning of the fourth day grain is brought again. 2 + 2 = 4 grains remain.
• At the end of the fourth day four sparrows come and eat grain. 4 - 4 = 0 grains remain. The barn is empty.

So the answer is 4, because by the end of the fourth day the barn becomes empty.

题意：给你一个谷仓容量为n，每天可以往里面添加m容量的谷子（多出部分就不要了），第i天会被吃掉i容量的谷子

　　　求第一次谷仓空的天数；

思路：显然，前m天谷仓还是满的，列出方程式；

　　　设答案为ans；

　　　n-1-2.....-（m-ans）<=ans；

　　　找到都一个ans，二分一下即可；详见代码；

#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<iostream>
#include<cstdio>
#include<cmath>
#include<string>
#include<queue>
#include<algorithm>
#include<stack>
#include<cstring>
#include<vector>
#include<list>
#include<set>
#include<map>
using namespace std;
#define ll long long
#define pi (4*atan(1.0))
#define eps 1e-14
#define bug(x)  cout<<"bug"<<x<<endl;
const int N=2e3+,M=1e6+,inf=1e9+;
const ll INF=1e17;
int main()
{
    ll n,m;
    scanf("%lld%lld",&n,&m);
    if(n<=m)
            return *printf("%lld\n",n);
    ll st=m;
    ll en=m+3e9+;
    ll ans;
    while(st<=en)
    {
        ll mid=(st+en)>>;
        if(n-(mid-m)*(mid-m-)/<=mid)
        {
            ans=mid;
            en=mid-;
        }
        else
            st=mid+;

    }
    printf("%lld\n",ans);
    return ;
}

D. Anton and School - 2

time limit per test

2 seconds

memory limit per test

256 megabytes

input

standard input

output

standard output

As you probably know, Anton goes to school. One of the school subjects that Anton studies is Bracketology. On the Bracketology lessons students usually learn different sequences that consist of round brackets (characters "(" and ")" (without quotes)).

On the last lesson Anton learned about the regular simple bracket sequences (RSBS). A bracket sequence s of length n is an RSBS if the following conditions are met:

• It is not empty (that is n ≠ 0).
• The length of the sequence is even.
• First  charactes of the sequence are equal to "(".
• Last  charactes of the sequence are equal to ")".

For example, the sequence "((()))" is an RSBS but the sequences "((())" and "(()())" are not RSBS.

Elena Ivanovna, Anton's teacher, gave him the following task as a homework. Given a bracket sequence s. Find the number of its distinct subsequences such that they are RSBS. Note that a subsequence of s is a string that can be obtained from s by deleting some of its elements. Two subsequences are considered distinct if distinct sets of positions are deleted.

Because the answer can be very big and Anton's teacher doesn't like big numbers, she asks Anton to find the answer modulo 109 + 7.

Anton thought of this task for a very long time, but he still doesn't know how to solve it. Help Anton to solve this task and write a program that finds the answer for it!

Input

The only line of the input contains a string s — the bracket sequence given in Anton's homework. The string consists only of characters "(" and ")" (without quotes). It's guaranteed that the string is not empty and its length doesn't exceed 200 000.

Output

Output one number — the answer for the task modulo 109 + 7.

Examples

input

)(()()

output

6

input

()()()

output

7

input

)))

output

0

Note

In the first sample the following subsequences are possible:

• If we delete characters at the positions 1 and 5 (numbering starts with one), we will get the subsequence "(())".
• If we delete characters at the positions 1, 2, 3 and 4, we will get the subsequence "()".
• If we delete characters at the positions 1, 2, 4 and 5, we will get the subsequence "()".
• If we delete characters at the positions 1, 2, 5 and 6, we will get the subsequence "()".
• If we delete characters at the positions 1, 3, 4 and 5, we will get the subsequence "()".
• If we delete characters at the positions 1, 3, 5 and 6, we will get the subsequence "()".

The rest of the subsequnces are not RSBS. So we got 6 distinct subsequences that are RSBS, so the answer is 6.

题意：给你一个括号序列

　　　找出所有的长度为偶数n，并且前n/2个为‘（’，后面n/2个为‘）’的字符串的个数；

思路：以（（））中间为分割线，枚举左边的那个括号；

　　　即对于每一个‘（’左边有x个，右边有y个右括号；

　　　（ps：对于当前的话‘（’是必须选的，所以不会造成重复的现象)

　　　

for(int j=;j<=x&&j+<=y;j++)
            ans=(ans+(com(x,j)*com(y,j+))%mod)%mod;
//对于暴力的写法，com为组合数学的C..x取j

令范德蒙恒等式

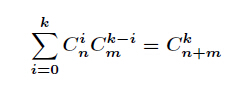
令n=x,m=y,k=y-1;

　　

#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<iostream>
#include<cstdio>
#include<cmath>
#include<string>
#include<queue>
#include<algorithm>
#include<stack>
#include<cstring>
#include<vector>
#include<list>
#include<set>
#include<map>
using namespace std;
#define ll long long
#define pi (4*atan(1.0))
#define eps 1e-14
#define bug(x)  cout<<"bug"<<x<<endl;
const int N=2e5+,M=1e6+,inf=;
const ll INF=1e18+,mod=1e9+;
char a[N];
ll A[N];
int l[N],r[N];
void init()
{
    A[]=1LL;
    for(int i=;i<=;i++)
        A[i]=(A[i-]*i)%mod;
}
ll quickpow(ll a,ll b)
{
    ll ans=;
    while(b)
    {
        if(b&)ans=(ans*a)%mod;
        b>>=;
        a=(a*a)%mod;
    }
    return ans;
}
ll com(int b,int a)
{
    return (A[b]*quickpow((A[b-a]*A[a])%mod,mod-))%mod;
}
int main()
{
    init();
    scanf("%s",a+);
    int n=strlen(a+);
    for(int i=;i<=n;i++)
        l[i]=l[i-]+(a[i]=='('?:);
    for(int i=n;i>=;i--)
        r[i]=r[i+]+(a[i]==')'?:);
    ll ans=;
    for(int i=;i<=n;i++)
    if(a[i]=='(')
    {
        //cout<<l[i-1]<<" "<<r[i]-1<<" "<<com(l[i-1]+r[i]-1,min(l[i-1],r[i]-1))<<endl;
        if(r[i])
        ans+=com(l[i-]+r[i],r[i]-);
        ans%=mod;
        /*int x=l[i-1];
        int y=r[i];
        for(int j=0;j<=x&&j+1<=y;j++)
            ans=(ans+(com(x,j)*com(y,j+1))%mod)%mod;*/
    }
    printf("%lld\n",ans);
    return ;
}

E. Anton and Permutation

time limit per test

4 seconds

memory limit per test

512 megabytes

input

standard input

output

standard output

Anton likes permutations, especially he likes to permute their elements. Note that a permutation of n elements is a sequence of numbers {a1, a2, ..., an}, in which every number from 1 to n appears exactly once.

One day Anton got a new permutation and started to play with it. He does the following operation q times: he takes two elements of the permutation and swaps these elements. After each operation he asks his friend Vanya, how many inversions there are in the new permutation. The number of inversions in a permutation is the number of distinct pairs (i, j) such that 1 ≤ i < j ≤ n and ai > aj.

Vanya is tired of answering Anton's silly questions. So he asked you to write a program that would answer these questions instead of him.

Initially Anton's permutation was {1, 2, ..., n}, that is ai = i for all i such that 1 ≤ i ≤ n.

Input

The first line of the input contains two integers n and q (1 ≤ n ≤ 200 000, 1 ≤ q ≤ 50 000) — the length of the permutation and the number of operations that Anton does.

Each of the following q lines of the input contains two integers li and ri (1 ≤ li, ri ≤ n) — the indices of elements that Anton swaps during the i-th operation. Note that indices of elements that Anton swaps during the i-th operation can coincide. Elements in the permutation are numbered starting with one.

Output

Output q lines. The i-th line of the output is the number of inversions in the Anton's permutation after the i-th operation.

Examples

input

5 4
4 5
2 4
2 5
2 2

output

1
4
3
3

input

2 1
2 1

output

1

input

6 7
1 4
3 5
2 3
3 3
3 6
2 1
5 1

output

5
6
7
7
10
11
8

Note

Consider the first sample.

After the first Anton's operation the permutation will be {1, 2, 3, 5, 4}. There is only one inversion in it: (4, 5).

After the second Anton's operation the permutation will be {1, 5, 3, 2, 4}. There are four inversions: (2, 3), (2, 4), (2, 5) and (3, 4).

After the third Anton's operation the permutation will be {1, 4, 3, 2, 5}. There are three inversions: (2, 3), (2, 4) and (3, 4).

After the fourth Anton's operation the permutation doesn't change, so there are still three inversions.

题意：给你n个数，q个询问，每次交换两个数，求逆序对的个数；

思路：分块+树状数组，数组数组求每块a[l],a[r]区间的数的个数，分块为了暴力怼；

#pragma comment(linker, "/STACK:1024000000,1024000000")
#include<iostream>
#include<cstdio>
#include<cmath>
#include<string>
#include<queue>
#include<algorithm>
#include<stack>
#include<cstring>
#include<vector>
#include<list>
#include<set>
#include<map>
using namespace std;
#define ll long long
#define pi (4*atan(1.0))
#define eps 1e-14
#define bug(x)  cout<<"bug"<<x<<endl;
const int N=2e5+,M=1e6+,inf=;
const ll INF=1e18+,mod=1e9+;
struct arraytree
{
    int tree[N];
    int lowbit(int x)
    {
        return x&-x;
    }
    void update(int x,int c)
    {
        while(x<N)
        {
            tree[x]+=c;
            x+=lowbit(x);
        }
    }
    int query(int x)
    {
        int ans=;
        while(x)
        {
            ans+=tree[x];
            x-=lowbit(x);
        }
        return ans;
    }
};
arraytree tree[];
int pos[N],k;
int a[N],n;
int query(int l,int r,int x,int y)
{
    if(l>r)return ;
    int ans=;
    if(pos[l]==pos[r])
    {
        for(int i=l;i<=r;i++)
            if(a[i]>x&&a[i]<y)
            ans++;
        return ans;
    }
    for(int i=l;i<=pos[l]*k&&i<=n;i++)
        if(a[i]>x&&a[i]<y)
            ans++;
    for(int i=(pos[r]-)*k+;i<=r;i++)
        if(a[i]>x&&a[i]<y)
            ans++;
    for(int i=pos[l]+;i<=pos[r]-;i++)
        ans+=tree[i].query(y)-tree[i].query(x-);
    return ans;
}
void update()
{

}
int main()
{
    int q;
    scanf("%d%d",&n,&q);
    k=sqrt(n);
    for(int i=;i<=n;i++)
        pos[i]=(i-)/k+,a[i]=i;
    for(int i=;i<=n;i++)
        tree[pos[i]].update(i,);
    ll ans=;
    while(q--)
    {
        int l,r;
        scanf("%d%d",&l,&r);
        if(l>r)swap(l,r);
        if(l==r)
        {
            printf("%lld\n",ans);
            continue;
        }
        int x=query(l+,r-,min(a[l],a[r]),max(a[l],a[r]));
        if(a[l]<a[r])
            ans+=*x+;
        else
            ans-=*x+;
        //cout<<"xxxx "<<x<<endl;
        printf("%lld\n",ans);
        if(pos[l]!=pos[r])
        {
            tree[pos[l]].update(a[l],-);
            tree[pos[l]].update(a[r],);
            tree[pos[r]].update(a[r],-);
            tree[pos[r]].update(a[l],);
        }
        swap(a[l],a[r]);
        //for(int i=1;i<=n;i++)
           // printf("%d ",a[i]);
        //cout<<endl;
    }
    return ;
}