luogu4705玩游戏

题解

我们要对于每个t，求一个(1/mn)sigma(ax+by)^t。

把系数不用管，把其他部分二项式展开一下：

simga(ax^r*by^(t-r)*C(t,r))。

把组合数拆开，就变成了一个卷积的形式。

t!*sigma((ax^r/r!)*(by^(t-r)/(t-r!))

不用管前面的系数，那么我们的卷积数组就是

sigma(ax^i)/i!

所以这道题本质让我们快速求f(i)=sigma(ax^i)。

考虑生成函数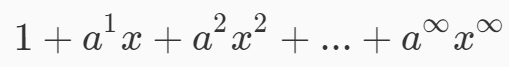

我们的f就是所有的这些生成函数的和。

然后上面的式子求和后变成

我们要求的就是所有这些东西的和。

考虑到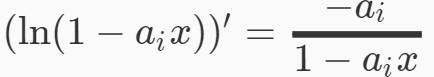

我么设G(x)为生面的式子，那么F(x)=-x*G(x)+n。

所以我们只需要求出G(x)就好了。

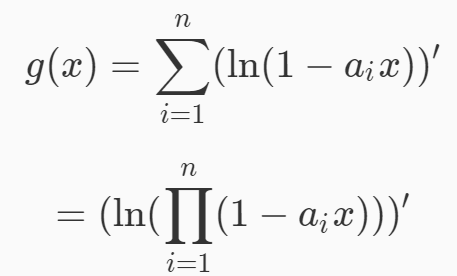
下面的那个连乘可以用分治乘法算出来，然后求个ln就好了。

代码

#include<iostream>
#include<cstdio>
#include<cstring>
#define N 550002
using namespace std;
typedef long long ll;
const ll mod=;
const ll G=;
const ll Gi=;
ll a[N],c[N],b[N],d[N],mem[][N],cnt,jie[N],ni[N],bu[N],t,bb[N],mp[N];
int rev[N],n,m;
inline int rd(){
    int x=;char c=getchar();bool f=;
    while(!isdigit(c)){if(c=='-')f=;c=getchar();}
    while(isdigit(c)){x=(x<<)+(x<<)+(c^);c=getchar();}
    return f?-x:x;
}
inline ll power(ll x,ll y){
    ll ans=;
    while(y){if(y&)ans=ans*x%mod;x=x*x%mod;y>>=;}
    return ans;
}
inline void NTT(ll *a,int l,int tag){
    for(int i=;i<l;++i)if(i>rev[i])swap(a[i],a[rev[i]]);
    for(int i=;i<l;i<<=){
        ll wn=power(tag==?G:Gi,(mod-)/(i<<));
        for(int j=;j<l;j+=(i<<)){
            ll w=;
            for(int k=;k<i;++k,w=w*wn%mod){
                ll x=a[j+k],y=a[i+j+k]*w%mod;
                a[j+k]=(x+y)%mod;a[i+j+k]=(x-y+mod)%mod;
            }
        }
    }
}
void solve(ll *a,int l,int r,ll *ans){
    if(l==r){ans[]=;ans[]=mod-a[l];return;}
    int mid=(l+r)>>;ll *a1=mem[++cnt];ll *a2=mem[++cnt];
    solve(a,l,mid,a1);solve(a,mid+,r,a2);
    int len=,L=;
    while(len<=*(r-l+))len<<=,L++;
    for(int i=;i<len;++i)rev[i]=(rev[i>>]>>)|((i&)<<(L-));
    NTT(a1,len,);NTT(a2,len,);
    for(int i=;i<len;++i)ans[i]=a1[i]*a2[i]%mod;
    NTT(ans,len,-);ll ny=power(len,mod-);
    for(int i=;i<len;++i)ans[i]=ans[i]*ny%mod,a1[i]=,a2[i]=;
    cnt-=;
}
void get_inv(ll *a,ll *b,int len){
    if(len==){b[]=power(a[],mod-);return;}
    get_inv(a,b,(len+)>>);
    int l=,L=;
    while(l<=(len<<))l<<=,L++;
    for(int i=;i<l;++i)rev[i]=(rev[i>>]>>)|((i&)<<(L-));
    for(int i=;i<len;++i)bu[i]=a[i];for(int i=len;i<l;++i)bu[i]=;
    NTT(bu,l,);NTT(b,l,);
    for(int i=;i<l;++i)b[i]=b[i]*(2ll-bu[i]*b[i]%mod+mod)%mod;
    NTT(b,l,-);ll ny=power(l,mod-);
    for(int i=;i<len;++i)b[i]=b[i]*ny%mod;for(int i=len;i<l;++i)b[i]=;
}
inline void get_dao(ll *a,int len){
    for(int i=;i<len;++i)a[i-]=a[i]*i%mod;a[len-]=;
}
inline void flag(ll *a,int len,ll *ans){
    int l=,L=;while(l<(max(len,(int)t)*))l<<=,L++;
    solve(a,,len,ans);
    get_inv(ans,b,t);get_dao(ans,l);//!!!!!!!!!!!!!
    for(int i=;i<l;++i)rev[i]=(rev[i>>]>>)|((i&)<<(L-));
    NTT(ans,l,);NTT(b,l,);
    for(int i=;i<l;++i)ans[i]=ans[i]*b[i]%mod;
    NTT(ans,l,-);ll ny=power(l,mod-);
    for(int i=;i<l;++i)ans[i]=ans[i]*ny%mod;
    for(int i=l-;i>=;--i)ans[i]=ans[i-]*(mod-)%mod;
    ans[]=len;
    for(int i=;i<=t;++i)ans[i]=ans[i]*ni[i]%mod;
    for(int i=t+;i<l;++i)ans[i]=;
}
int main(){
    n=rd();m=rd();
    for(int i=;i<=n;++i)a[i]=rd();
    for(int i=;i<=m;++i)bb[i]=rd();
    t=rd();
    jie[]=;for(int i=;i<=t;++i)jie[i]=jie[i-]*i%mod;ni[t]=power(jie[t],mod-);
    for(int i=t-;i>=;--i)ni[i]=ni[i+]*(i+)%mod;
    flag(a,n,c);memset(b,,sizeof(b));flag(bb,m,d);
    int l=,L=;
    while(l<=t*)l<<=,L++;
    for(int i=;i<l;++i)rev[i]=(rev[i>>]>>)|((i&)<<(L-));
    NTT(c,l,);NTT(d,l,);
    for(int i=;i<l;++i)c[i]=c[i]*d[i]%mod;
    NTT(c,l,-);ll ny=power(l,mod-);
    for(int i=;i<l;++i)c[i]=c[i]*ny%mod;
    ny=power(1ll*n*m%mod,mod-);
    for(int i=;i<=t;++i)printf("%lld\n",c[i]*jie[i]%mod*ny%mod);
    return ;
}