Stanford Local 2016 E "Election of Evil"（搜索（正解）或并查集（划掉））

传送门

题意：

　　给出集合U,V，集合U有n个元素，集合V有m个元素；

　　有 m 个操作，m_i : s₁ s₂ 有一条s₁指向s₂的边（s₁,s₂可能属于第三个集合，暂且称之为K集合）；

　　指向边具有传递性，即 A->B,B->C <=> A->C

　　求V集合中被 U 指向的元素；

题解：

　　并查集debug个了两天，始终wa，今天上午上数字逻辑课的时候，灵光一闪，又想到了一个可能会出错的点；

　　经过一番挣扎，终于判断了此题不能用并查集做，蓝瘦香菇~~~~~~

　　还记得并查集中的Union(x,y)操作吗？

　　此函数得作用是将 x元素 所在的集合与 y元素 所在得集合合并成一个大集合；

　　对于此题，初始想法是，并查集中只保存

　　　　①U 集合指出去的边

　　　　②K 集合指向 V 集合的边

　　　　③V 集合指向 V 集合的边

　　如果满足上述三种条件，则Union(s₁,s₂)；

　　最后，判断V集合中元素的Find(s)是否属于U集合，如果属于，则输出s；

　　那么，问题来了，s₁,s₂真的可以这么合并吗？

　　看如下连接方式：

　　

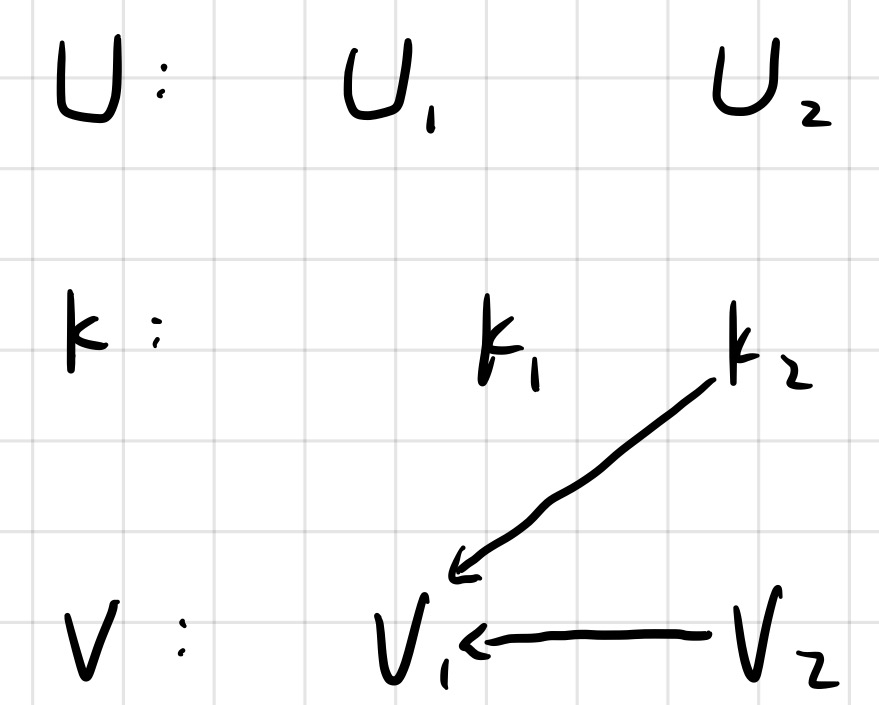
　　输入的顺序是：

　　　　v₂ v₁

　　　　k₂ v₁

　　对于第一条指令，Union(v₂,v₁)是没得说的，此时 fa(v₁) = v₂ , fa(v₂) =v₂；

　　对于第二条指令，可以调用 Union(k₂,v₁) 吗？

　　先看看调用后的结果：Find(k₂) = k₂ , Find(v₁) = v₂ , k₂ ≠ v₂ , fa(v₁)=fa(v₂)=k_2； ???

　　那么，再加入一条边呢？

　　　　u₁ k₂

　　

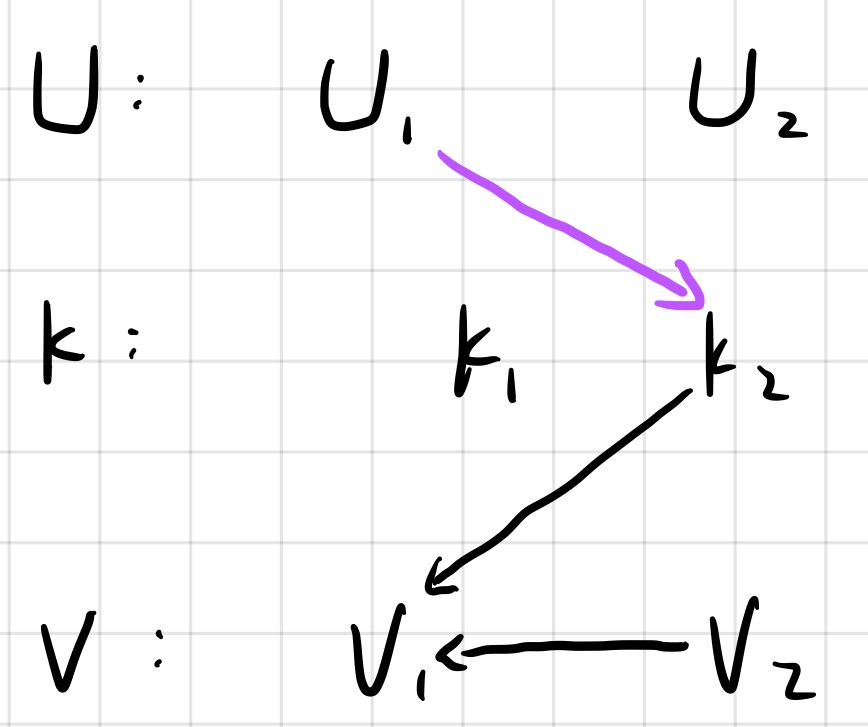
　　那么，此时调用Union(u₁,k₂) : fa(k₂) = u₁;

　　当输出时：

　　　　v₁ : Find(v₁) = Find(k₂) = u₁ ，输出 v₁

　　　　v₂ : Find(v₂) = Find(k₂) = u₁ ，输出 v₂

　　这就出现问题了吧！！！

　　那，如果人为的将 fa(v₁) = k₂，但是fa(v₂) = v₂呢？

　　看一下接下来的这张图：

　　加入边 u₂ v₂

　　

　　

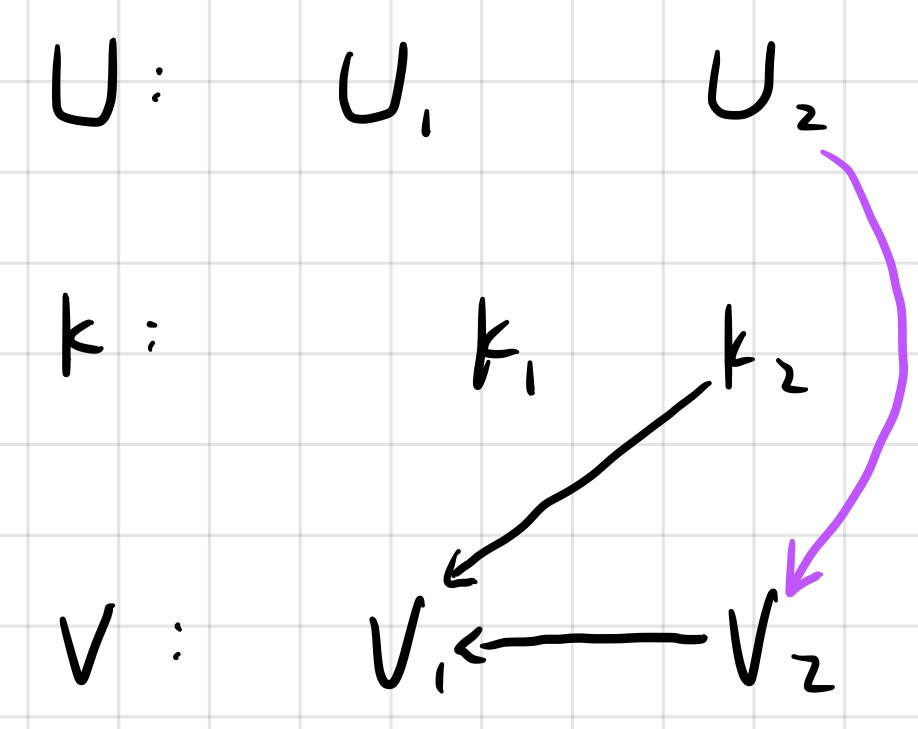
　　输出时：

　　　　v₁ : Find(v₁) = k₂ ，不输出 v₁

　　　　v₂ : Find(v₂) = u₂ ，输出 v₂

　　又出现错误了，是吧！

　　为什么并查集会出现这个问题呢？

　　v₁,v₂属于同一个集合，v₁,k₂属于同一个集合，但 k₂,v₂并不能属于同一个集合，所以不能合并；

　　看来，当图是有向图时，慎用并查集!!!!!!!!!!!!!

　　

　　所以说，还是搜索大法好！！！！

AC代码：

 #include<iostream>
 #include<cstdio>
 #include<map>
 #include<cstring>
 using namespace std;
 #define mem(a,b) memset(a,b,sizeof(a))
 const int maxn=1e4+;

 int n,m,x;
 int numU,numV;//[1,numU]集合U的编号范围，[numU+1,numV]:集合V的编号范围
 bool vis[maxn];//vis[i]:判断属于V集合的编号i是否有条被U集合指向的边
 bool rep[maxn];//rep[i]:判断i编号对应的字符串是否重复出现在U,V集合中
 int head[maxn];
 int num;
 struct Edge
 {
     int to;
     int next;
 }G[*maxn];
 void addEdge(int u,int v)
 {
     G[num].to=v;
     G[num].next=head[u];
     head[u]=num++;
 }
 map<string ,int >mymap;//将字符串映射成整数

 bool isSetU(int xx)//判断节点xx是否属于U集合
 {
     return xx >=  && xx <= numU;
 }
 bool isSetV(int xx)//判断节点xx是否属于V集合
 {
     return xx > numU && xx <= numV;
 }
 void DFS(int u)
 {
     vis[u]=true;//被集合U指向的节点
     for(int i=head[u];~i;i=G[i].next)
     {
         int v=G[i].to;
         if(!vis[v])
             DFS(v);
     }
 }
 void Solve(int id)
 {
     for(int i=;i <= x;++i)
     {
         string s1,s2;
         cin>>s1>>s2;
         if(!mymap.count(s1))
             mymap[s1]=++id;
         if(!mymap.count(s2))
             mymap[s2]=++id;
         int u=mymap[s1];
         int v=mymap[s2];
         addEdge(u,v);
     }
     map<string ,int>::iterator it;
     for(it=mymap.begin();it != mymap.end();++it)
     {
         int x=it->second;
         if(!isSetU(x) || vis[x])
             continue;
         //以集合U中的元素为起点开始搜索
         DFS(x);
     }
     bool flag=false;
     for(it=mymap.begin();it != mymap.end();++it)
     {
         int x=it->second;
         if(rep[x] || isSetV(x)&&vis[x])
         {
             if(!flag)
                 cout<<it->first;
             else
                 cout<<" "<<it->first;
             flag=true;
         }
     }
     cout<<"\n";
 }
 void Init()
 {
     num=;
     mem(head,-);
     mem(rep,false);
     mem(vis,false);
     mymap.clear();
 }
 int main()
 {
 //    freopen("C:\\Users\\hyacinthLJP\\Desktop\\in&&out\\contest","r",stdin);
     ios::sync_with_stdio(false);
     cin.tie();
     cout.tie();

     int test;
     cin>>test;
     while(test--)
     {
         Init();
         cin>>n>>m>>x;
         int id=;
         for(int i=;i <= n;++i)
         {
             string s;
             cin>>s;
             mymap[s]=++id;
         }
         numU=id;
         for(int i=;i <= m;++i)
         {
             string s;
             cin>>s;
             if(!mymap.count(s))
                 mymap[s]=++id;
             else
                 rep[mymap[s]]=true;//重复出现的字符串
         }
         numV=id;
         Solve(id);
     }
     return ;
 }