DP基础练习(4.21)

数塔

Description

在讲述DP算法的时候，一个经典的例子就是数塔问题，它是这样描述的：

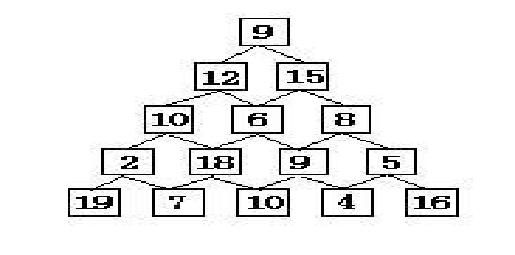
有如下所示的数塔，要求从顶层走到底层，若每一步只能走到相邻的结点，则经过的结点的数字之和最大是多少？

Input

输入数据首先包括一个整数C,表示测试实例的个数，每个测试实例的第一行是一个整数N(1 <= N <= 100)，表示数塔的高度，接下来用N行数字表示数塔，其中第i行有个i个整数，且所有的整数均在区间[0,99]内。

Output

对于每个测试实例，输出可能得到的最大和，每个实例的输出占一行。

Sample Input 1

Sample Output 1

 #include <cstdio>
 #include <algorithm> 

 using namespace std;

 int main()
 {
     int c;
     scanf("%d",&c);
     while(c--)
     {
         int a[][]={};
         int dp[][]={};
         int n;
         scanf("%d",&n);
         for(int i=;i<=n;i++)
         {
             for(int j=;j<=i;j++)
             {
                 scanf("%d",&a[i][j]);
             }
         }
         for(int i=;i<=n;i++)
         {
             dp[n][i]=a[n][i];
         }
         for(int i=n-;i>=;i--)
         {
             for(int j=;j<=i;j++)
             {
                 dp[i][j]=max(dp[i+][j],dp[i+][j+])+a[i][j];
             }
         }
         printf("%d\n",dp[][]);
     }
     return ;
 }

音量调节

Description

一个吉他手准备参加一场演出。他不喜欢在演出时始终使用同一个音量，所以他决定每一首歌之前他都要改变一次音量。在演出开始之前，他已经做好了一个列表，里面写着在每首歌开始之前他想要改变的音量是多少。每一次改变音量，他可以选择调高也可以调低。
音量用一个整数描述。输入文件中给定整数beginLevel，代表吉他刚开始的音量，以及整数maxLevel，代表吉他的最大音量。音量不能小于0也不能大于maxLevel。输入文件中还给定了n个整数c1,c2,c3…..cn，表示在第i首歌开始之前吉他手想要改变的音量是多少。
吉他手想以最大的音量演奏最后一首歌，你的任务是找到这个最大音量是多少。

Input

第一行依次为三个整数：n, beginLevel, maxlevel。
第二行依次为n个整数：c1,c2,c3…..cn。

Output

输出演奏最后一首歌的最大音量。如果吉他手无法避免音量低于0或者高于maxLevel，输出-1。

Sample Input

3 5 10 
5 3 7

Sample Output

10

HINT

1<=N<=50,1<=Ci<=Maxlevel 1<=maxlevel<=1000

0<=beginlevel<=maxlevel

Source

一开始便开始想用f[i]表示前i个物品能够得到的最大的音量，以为和装箱问题一样。于是借用一下强大的搜索引擎，发现一种叫布尔型dp，就是用f[i][j]表示前i个物品在音量为j时可行；记住这种表示方式；

 #include <iostream>
 #include <cstring>
 #include <algorithm> 

 using namespace std;

 int a[];
 bool dp[][];

 int main()
 {
     int n,initial,maxl;
     cin>>n>>initial>>maxl;
     for(int i=;i<=n;i++)
     {
         cin>>a[i];
     }
     memset(dp,false,sizeof(dp));
     dp[][initial]=true;
     for(int i=;i<=n;i++)
     {
         for(int j=;j<=maxl;j++)
         {
             //dp[i][j]是第i次调节可以获得的音量j
             dp[i][j]=((j+a[i]<=maxl)&&dp[i-][j+a[i]])||((j-a[i]>=)&&dp[i-][j-a[i]]);
             //j+a[i]<=maxl和 j-a[i]>=0判断是否超出dp[]的范围
             //dp[i-1][j+a[i]]为真说明第i次调节后的j可以是第i-1次的某个音量减去a[i]得到
             //dp[i-1][j-a[i]]为真说明第i次调节后的j可以是第i-1次的某个音量加上a[i]得到
         }
     }
     for(int i=maxl;i>=;i--)
     {
         if(dp[n][i])
         {
             cout<<i<<endl;
             return ;
         }
     }
     cout<<-<<endl;
     return ;
 }

消失之物

Description
ftiasch 有 N 个物品, 体积分别是 W1, W2, ..., WN。 由于她的疏忽, 第 i 个物品丢失了。 “要使用剩下的 N - 1 物品装满容积为 x 的背包，有几种方法呢？” -- 这是经典的问题了。她把答案记为 Count(i, x) ，想要得到所有1 <= i <= N, 1 <= x <= M的 Count(i, x) 表格。

Input
 
第1行：两个整数 N (1 ≤ N ≤ 2 × 103) 和 M (1 ≤ M ≤ 2 × 103)，物品的数量和最大的容积。

第2行： N 个整数 W1, W2, ..., WN, 物品的体积。

Output
 
一个 N × M 的矩阵， Count(i, x)的末位数字。

Sample Input
3 2
1 1 2
Sample Output
11
11
21
HINT
如果物品3丢失的话，只有一种方法装满容量是2的背包，即选择物品1和物品2。

题解
先考虑不删除物品怎么做，其实就是一个背包，dp[i][j]=dp[i-1][j]+dp[i-1][j-w[i]];那么现在考虑少了物品i会减少几种方案，当x小于w[i]时，i物品一定不会被选上 g[i]=f[i] 当x大于等于w[i]时，i物品可能会被选上，直接求不选的情况比较困难。可以换个思路，设g[x]为不选当前物品的容量为x的方案数，用总方案数-选的方案数得到不选的方案数。总方案数及f[x]，不选的方案数可以想为先不选i再最后把i选上,即g[x-w[i]]。

 #include<cstdio>
 #include<algorithm>
 #include<cstring>
 #include<iostream>
 using namespace std;
 const int N=;
 int f[N],g[N],w[N];
 int n,m;
 int main(){
     scanf("%d%d",&n,&m);
     for(int i=;i<=n;i++) scanf("%d",&w[i]);

     f[]=;
     for(int i=;i<=n;i++){
         for(int j=m;j>=w[i];j--)
         f[j]=(f[j]+f[j-w[i]])%;
     }
     for(int i=;i<=n;i++){
         for(int j=;j<=m;j++){
             if(j<w[i]) g[j]=f[j];
             else g[j]=(f[j]-g[j-w[i]]+)%;
         }
         for(int j=;j<=m;j++) printf("%d",g[j]);
         printf("\n");
     }
     return ;
 }

分析

很明显是个01背包的dp,但是问题在于统计这个答案上。感觉和容斥原理略有关系？于是研读了一下黄学长的极妙的做法

首先，f[j]表示装满容积为j的背包的方案数 很明显，f[j]+=f[j-w[i]] (f[0]=1)

统计答案我们用c[i][j]表示

再枚举I,j

如果f[j]<w[i]，显然，装满容积j显然不可能用到第i个物品，所以c[i][j]=f[j]。

如果f[j]>=w[i],f[j]里就包括了选择了第i件物品的情况，那我们需要扣除掉这一部分。把扣除的这部分转换一下：

用第i件物品填满j ---> 用了其他物品填了j-w[i]，所以c[i][j]=f[j]-c[i][j-w[i]]

 #include<bits/stdc++.h>
 using namespace std;
 #define N 2020
 int n,m;
 int f[N],w[N];
 int    c[N][N];
 int main()
 {
     scanf("%d%d",&n,&m);
     for(int i=;i<=n;i++)
         scanf("%d",&w[i]);
     f[]=;
     for(int i=;i<=n;i++)
         for(int j=m;j>=w[i];j--)
             f[j]+=f[j-w[i]],f[j]%=;
     for(int i=;i<=n;i++)
     {
         c[i][]=;
         for(int j=;j<=m;j++)
         {
             if(j>=w[i])c[i][j]=(f[j]-c[i][j-w[i]]+)%;
             else    c[i][j]=f[j];
             printf("%d",c[i][j]);
         }
         printf("\n");
     }
     return ;
 }

货币系统

在网友的国度中共有 n 种不同面额的货币，第 i 种货币的面额为 a[i]，你可以假设每一种货币都有无穷多张。为了方便，我们把货币种数为 n、面额数组为 a[1…n] 的货币系统记作 (n,a)。

在一个完善的货币系统中，每一个非负整数的金额 x 都应该可以被表示出，即对每一个非负整数 x，都存在 n 个非负整数 t[i] 满足 a[i]×t[i] 的和为 x。然而， 在网友的国度中，货币系统可能是不完善的，即可能存在金额 x 不能被该货币系统表示出。例如在货币系统 n=3, a=[2,5,9] 中，金额 1,3 就无法被表示出来。

两个货币系统 (n,a) 和 (m,b) 是等价的，当且仅当对于任意非负整数 x，它要么均可以被两个货币系统表出，要么不能被其中任何一个表出。

现在网友们打算简化一下货币系统。他们希望找到一个货币系统 (m,b)，满足 (m,b) 与原来的货币系统 (n,a) 等价，且 m 尽可能的小。他们希望你来协助完成这个艰巨的任务：找到最小的 m。

输入
输入文件的第一行包含一个整数 T，表示数据的组数。
接下来按照如下格式分别给出 T 组数据。 每组数据的第一行包含一个正整数 n。接下来一行包含 n 个由空格隔开的正整数 a[i]。

输出
输出文件共有 T 行，对于每组数据，输出一行一个正整数，表示所有与 (n,a) 等价的货币系统 (m,b) 中，最小的 m。

输入

输出

说明

在第一组数据中，货币系统(2, [3,10])和给出的货币系统(n, a)等价，并可以验证不存在m < 2的等价的货币系统，因此答案为2。
在第二组数据中，可以验证不存在m < n的等价的货币系统，因此答案为5。

备注:

1 <= T <= 20, 1 <= n <= 100, 1 <= a[i] <= 25000

解题思路
题目说的很长，其实题目的大意就是有 n nn 个数，然后让你找 m mm 个数使得这 m mm 个数与 n nn 个数的表示范围相同。那么我们来分析一下，首先相同的数字肯定是没有意义的，我们对原数组进行去重，然后我们用一个数组 vis[i] vis[i]vis[i] 表示数字 i ii 是否能够表示，如果 vis[i]=true vis[i]=truevis[i]=true 可以表示，否则不可以表示。那么我们就对于 n nn 个数中的每一个数字进行判断，第一个 a[0] a[0]a[0] 肯定不能表示，那么我们结果 ans++ ans++ans++， 然后把 a[0] a[0]a[0] 能够表示的数字 i ii 全标记为 vis[i]=true vis[i]=truevis[i]=true；那么在检查第 i ii 个数字，如果能够用已经标记的数字表示，那么说明这个数可以用 之前的数表示，答案不记录；否则答案记录，而且将已经能够表示的数字加上 a[i] a[i]a[i]，也进行标记 vis[j+a[i]]=true vis[j+a[i]]=truevis[j+a[i]]=true，直至循环完毕，输出 ans ansans 即可。

 #include <iostream>
 #include <stdio.h>
 #include <string.h>
 #include <stdlib.h>
 #include <math.h>
 #include <set>
 #include <vector>
 #include <algorithm>
 #define pb push_back
 #define mk make_pair
 #define fi first
 #define se second
 using namespace std;
 typedef pair<int, int> pii;
 typedef long long LL;
 typedef unsigned long long ULL;
 const int MAXN = +;
 int a[];
 bool vis[MAXN];
 int main() {
     int T; cin>>T;
     while(T--) {
         int n; cin>>n;
         for(int i=; i<n; i++) cin>>a[i];
         sort(a, a+n);
         n = unique(a, a+n)-a;
         memset(vis, false, sizeof vis);
         vis[] = true;
         int ans = ;
         for(int i=; i<n; i++) {
             if(!vis[a[i]]) {
                 ans++;
                 for(int j=; j<MAXN; j++) if(j+a[i]<=&&vis[j]) vis[j+a[i]] = true;
             }
         }
         cout<<ans<<endl;
     }
     return ;
 }

题解
首先我想弱弱地说一句，比赛的时候我并没有看懂这道题，也就是说没有思路说多了都是泪

但是我下来想了一下，这道题可以用背包来做

递推式（转移方程）为f[i]=max(f[i],f[i−money[j]]+1)

f[i]表示i面值最多能被几张钱表示

f[i]=-inf表示有且只有它自己则f[i]=1

在开始之前初始化f[0]=0

就是这样~

 #include<iostream>
 #include<cstring>
 using namespace std;
 int a[], n;
 int ans;
 int f[];
 int main() {
     //freopen("money.in","r",stdin);
     //freopen("money.out","w",stdout);
     int T;
     cin >> T;
     for(int k = ; k <= T; k++) {
         memset(f, -, sizeof f);
         ans = ;
         cin >> n;
         for(int i=; i<=n; i++)
             cin >> a[i];
         f[] = ;
         for(int i = ; i <= n; i++) {
             for(int j = a[i]; j <= ; j++) {
                 f[j] = max(f[j], f[j - a[i]] + );
             }
         }
         for(int i = ; i <= n; i++)
             if(f[a[i]] == ) {
                 ans++;
             }
         cout << ans << endl;
     }
 }
  

一个结论性的题目……吧。

首先手推一下，发现新货币系统中的最小值 m′ m'm
′
一定等于原来的货币系统中的最小值 m mm。如果大于，则新货币系统无法表达 m mm；如果小于，则原货币系统无法表达 m′ m'm
′
。

然后我们递归性地猜想：假如我去掉了这个最小值以及最小值能表达的数（因为新货币系统里面如果再有这些数就不够优秀了），那么再选择最小值是否也一定是最优的？
仿照上面的证明可以发现这个推论是正确的。

因此我们就可以得到我们的算法：
（1）找到原货币系统当前的最小值，加入新货币系统。
（2）在原货币系统中删除新货币系统能表达的数。
循环（1），（2）直到原货币系统没有任何数。

我们实现上可以不按这么写。我们可以从小到大枚举原货币系统中的数，判断它能否被新货币系统表达。能则跳过；不能则更新新货币系统。
判断以及更新可以用完全背包来做。

 #include<cstdio>
 #include<algorithm>
 using namespace std;
 const int MAXN = ;
 const int MAXM = ;
 bool dp[MAXM + ];
 int a[MAXN + ];
 void solve() {
     int n, m = , lim = ;
     scanf("%d", &n);
     for(int i=;i<=n;i++) {
         scanf("%d", &a[i]);
         lim = max(lim, a[i]);
     }
     for(int i=;i<=lim;i++)
         dp[i] = false;
     sort(a+, a+n+); dp[] = true;
     for(int i=;i<=n;i++) {
         if( !dp[a[i]] ) {
             for(int j=a[i];j<=lim;j++)
                 dp[j] |= dp[j-a[i]];
             m++;
         }
     }
     printf("%d\n", m);
 }
 int main() {
     int T;
     scanf("%d", &T);
     for(int i=;i<=T;i++)
         solve();
     return ;
 }