すぬけ君の塗り絵 / Snuke's Coloring AtCoder - 2068 （思维，排序，贡献）

Problem Statement

We have a grid with H rows and W columns. At first, all cells were painted white.

Snuke painted N of these cells. The i-th ( 1≤i≤N ) cell he painted is the cell at the a_i-th row and b_i-th column.

Compute the following:

• For each integer j ( 0≤j≤9 ), how many subrectangles of size 3×3 of the grid contains exactly j black cells, after Snuke painted N cells?

Constraints

• 3≤H≤10⁹
• 3≤W≤10⁹
• 0≤N≤min(10⁵,H×W)
• 1≤a_i≤H (1≤i≤N)
• 1≤b_i≤W (1≤i≤N)
• (a_i,b_i)≠(a_j,b_j) (i≠j)

Input

The input is given from Standard Input in the following format:

H W N
a1 b1
:
aN bN

Output

Print 10 lines. The (j+1)-th ( 0≤j≤9 ) line should contain the number of the subrectangles of size 3×3 of the grid that contains exactly j black cells.

Sample Input 1

4 5 8
1 1
1 4
1 5
2 3
3 1
3 2
3 4
4 4

Sample Output 1

0
0
0
2
4
0
0
0
0
0

There are six subrectangles of size 3×3. Two of them contain three black cells each, and the remaining four contain four black cells each.

Sample Input 2

10 10 20
1 1
1 4
1 9
2 5
3 10
4 2
4 7
5 9
6 4
6 6
6 7
7 1
7 3
7 7
8 1
8 5
8 10
9 2
10 4
10 9

Sample Output 2

4
26
22
10
2
0
0
0
0
0

Sample Input 3

1000000000 1000000000 0

Sample Output 3

999999996000000004
0
0
0
0
0
0
0
0
0

题意：
给定一个高为h，宽为w的矩阵，然后给你n个黑色块的坐标。
让你求出所有大小为3*3的矩阵分别包含了多少个黑色块，
你只需要输出含有0~9个黑色块的个数的矩阵数量分别是多少。

思路：
由于h和w的数量很大，没有办法进行直接标记模拟。、
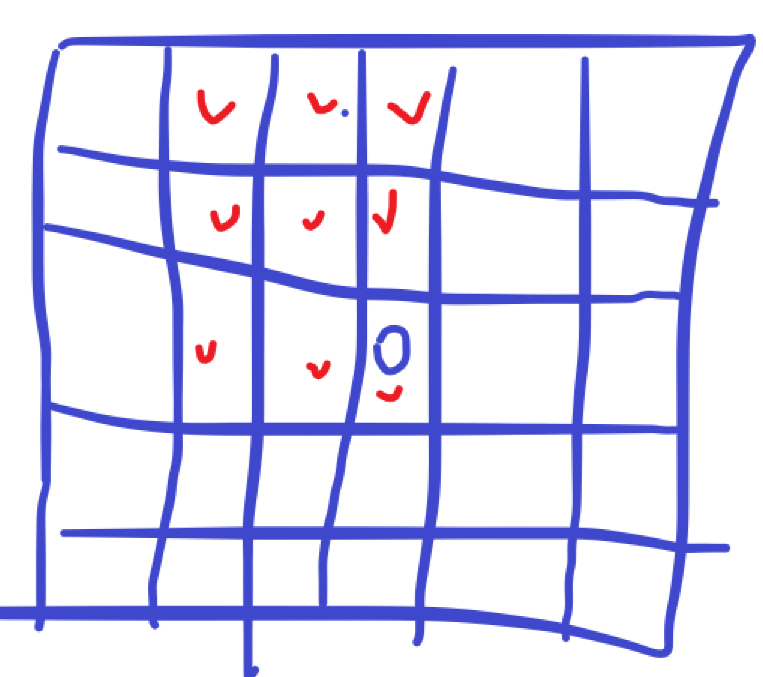
我们思考如下：每一个黑色的方块只会对9个3*3的矩阵有贡献。

看图：

看图可以知道，蓝色圆圈的位置如果是黑色块，可以对以红色点为左上角起点的3*3的区间有贡献。

那么我们对每一个黑色块算出的一共9个的贡献矩阵，全部加入到一个数组中，排序后处理答案即可。

细节见代码：

#include <iostream>
#include <cstdio>
#include <cstring>
#include <algorithm>
#include <cmath>
#include <queue>
#include <stack>
#include <map>
#include <set>
#include <vector>
#include <iomanip>
#define ALL(x) (x).begin(), (x).end()
#define rt return
#define dll(x) scanf("%I64d",&x)
#define xll(x) printf("%I64d\n",x)
#define sz(a) int(a.size())
#define all(a) a.begin(), a.end()
#define rep(i,x,n) for(int i=x;i<n;i++)
#define repd(i,x,n) for(int i=x;i<=n;i++)
#define pii pair<int,int>
#define pll pair<long long ,long long>
#define gbtb ios::sync_with_stdio(false),cin.tie(0),cout.tie(0)
#define MS0(X) memset((X), 0, sizeof((X)))
#define MSC0(X) memset((X), '\0', sizeof((X)))
#define pb push_back
#define mp make_pair
#define fi first
#define se second
#define eps 1e-6
#define gg(x) getInt(&x)
#define db(x) cout<<"== [ "<<x<<" ] =="<<endl;
using namespace std;
typedef long long ll;
ll gcd(ll a,ll b){return b?gcd(b,a%b):a;}
ll lcm(ll a,ll b){return a/gcd(a,b)*b;}
ll powmod(ll a,ll b,ll MOD){ll ans=;while(b){if(b%)ans=ans*a%MOD;a=a*a%MOD;b/=;}return ans;}
inline void getInt(int* p);
const int maxn=;
const int inf=0x3f3f3f3f;
/*** TEMPLATE CODE * * STARTS HERE ***/
struct node
{
    ll x,y;
}a[maxn];
ll n;
ll h,w;
ll xx[]={-,-,-,-,-,-,,,};
ll yy[]={-,-,,-,-,,-,-,};
ll ans[];
ll mod=1e9+;
int main()
{
    //freopen("D:\\common_text\\code_stream\\in.txt","r",stdin);
    //freopen("D:\\common_text\\code_stream\\out.txt","w",stdout);
    gbtb;
    cin>>h>>w>>n;
    repd(i,,n)
    {
        cin>>a[i].x>>a[i].y;
    }
    vector<ll> v;
    repd(i,,n)
    {
        repd(j,,)
        {
            ll x=a[i].x+xx[j];
            ll y=a[i].y+yy[j];
            if(x>=&&x+<=h&&y>=&&y+<=w)
            {
//                cout<<x<<" "<<y<<endl;
                ll num=(x)*mod+y;
                v.push_back(num);
            }
        }
    }
    sort(ALL(v));
    v.push_back(-9ll);
    ll ww=1ll;
    ll ans0=(h-2ll)*(w-2ll);
    for(int i=;i<v.size()-;i++)
    {
//        db(v[i]);
        if(v[i]==v[i+])
        {
            ww++;
        }else
        {
            ans[ww]++;
            ww=1ll;
            ans0--;
        }
    }
    cout<<ans0<<endl;
    repd(i,,)
    {
        cout<<ans[i]<<endl;
    }

    return ;
}

inline void getInt(int* p) {
    char ch;
    do {
        ch = getchar();
    } while (ch == ' ' || ch == '\n');
    if (ch == '-') {
        *p = -(getchar() - '');
        while ((ch = getchar()) >= '' && ch <= '') {
            *p = *p *  - ch + '';
        }
    }
    else {
        *p = ch - '';
        while ((ch = getchar()) >= '' && ch <= '') {
            *p = *p *  + ch - '';
        }
    }
}