loj 3090 「BJOI2019」勘破神机 - 数学

题目传送门

　　传送门

题目大意

　　设$F_{n}$表示用$1\times 2$的骨牌填$2\times n$的网格的方案数，设$G_{n}$表示用$1\times 2$的骨牌填$3\times n$的网格的方案数.

• 给定$l, r, k$，求$\frac{1}{r - l + 1}\sum_{i = l}^{r} \binom{F_{i}}{k}$.
• 给定$l, r, k$，求$\frac{1}{r - l + 1}\sum_{i = l}^{r} \binom{G_{i}}{k}$.

　　之前好像在loj / uoj群上问过求Fibonacci求立方和。sad。。。

　　校内考的时候忘了求数列通项，sad。。。

　　首先用Stirling数把组合数拆成通常幂。

　　对于第一部分，直接用$Fibonacci$通项，由于$5$不是模$998244353$的二次剩余，所以把答案在运算中表示成$a + b\sqrt{5}$的形式。

　　第$n$项的$k$次幂大概是$(a^n + b^n)^{K}$，这个不方便直接求和。用二项式定理展开就行了。

　　对于第二部分。考察选手是否上过高考数学课（bushi

　　显然当$2 \nmid n$时$G_{n} = 0$，现在考虑$G'_{n} = G_{2n}$。

　　注意到最后只有这几种填法：

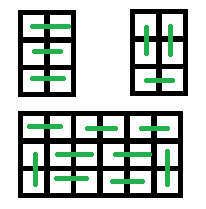
　　所以有

$$
\begin{align}
G'_{n} &= 3G_{n - 1} + 2\sum_{i = 0}^{n - 2}G_{i} \\
&= 4G_{n - 1} - 3G_{n - 2} - 2\sum_{i = 0}^{n - 3} G_{i - 1} + 2\sum_{i =0}^{n - 2}G_i \\
&= 4G_{n - 1} - G_{n - 2}
\end{align}
$$

　　用特征根法推通项（不会的话可以回教室了）。然后做完了。

　　（我被Jode锤爆了。瑟瑟发抖.jpg）

Code

#include <bits/stdc++.h>
using namespace std;
typedef bool boolean;

#define ll long long

void exgcd(int a, int b, int& x, int& y) {
	if (!b) {
		x = 1, y = 0;
	} else {
		exgcd(b, a % b, y, x);
		y -= (a / b) * x;
	}
}

int inv(int a, int n) {
	int x, y;
	exgcd(a, n, x, y);
	return (x < 0) ? (x + n) : (x);
}

const int Mod = 998244353;

template <const int Mod = :: Mod>
class Z {
	public:
		int v;

		Z() : v(0) {	}
		Z(int x) : v(x){	}
		Z(ll x) : v(x % Mod) {	}

		friend Z operator + (const Z& a, const Z& b) {
			int x;
			return Z(((x = a.v + b.v) >= Mod) ? (x - Mod) : (x));
		}
		friend Z operator - (const Z& a, const Z& b) {
			int x;
			return Z(((x = a.v - b.v) < 0) ? (x + Mod) : (x));
		}
		friend Z operator * (const Z& a, const Z& b) {
			return Z(a.v * 1ll * b.v);
		}
		friend Z operator ~(const Z& a) {
			return inv(a.v, Mod);
		}
		friend Z operator - (const Z& a) {
			return Z(0) - a;
		}
		Z& operator += (Z b) {
			return *this = *this + b;
		}
		Z& operator -= (Z b) {
			return *this = *this - b;
		}
		Z& operator *= (Z b) {
			return *this = *this * b;
		}
		friend boolean operator == (const Z& a, const Z& b) {
			return a.v == b.v;
		}
};

Z<> qpow(Z<> a, int p) {
	Z<> rt = Z<>(1), pa = a;
	for ( ; p; p >>= 1, pa = pa * pa) {
		if (p & 1) {
			rt = rt * pa;
		}
	}
	return rt;
}

typedef Z<> Zi;

template <const int I>
class ComplexTemp {
	public:
		Zi r, v;

		ComplexTemp() : r(0), v(0) {	}
		ComplexTemp(Zi r) : r(r), v(0) {	}
		ComplexTemp(Zi r, Zi v) : r(r), v(v) {	}

		friend ComplexTemp operator + (const ComplexTemp& a, const ComplexTemp& b) {
			return ComplexTemp(a.r + b.r, a.v + b.v);
		}
		friend ComplexTemp operator - (const ComplexTemp& a, const ComplexTemp& b) {
			return ComplexTemp(a.r - b.r, a.v - b.v);
		}
		friend ComplexTemp operator - (const ComplexTemp& a, const int& b) {
			return ComplexTemp(a.r - b, a.v);
		}
		friend ComplexTemp operator * (const ComplexTemp& a, const ComplexTemp& b) {
			return ComplexTemp(a.r * b.r + a.v * b.v * I, a.r * b.v + a.v * b.r);
		}
		friend ComplexTemp operator * (const ComplexTemp& a, const Zi& x) {
			return ComplexTemp(a.r * x, a.v * x);
		}
		friend ComplexTemp operator / (const ComplexTemp& a, const ComplexTemp& b) {
			ComplexTemp c = b.conj();
			return a * c * ~((b * c).r);
		}
		ComplexTemp conj() const {
			return ComplexTemp(r, -v);
		}
		boolean operator == (ComplexTemp b) {
			return r == b.r && v == b.v;
		}
};

const int Kmx = 510;

Zi s1[Kmx][Kmx];
Zi comb[Kmx][Kmx];
Zi fac[Kmx], _fac[Kmx];
void prepare(int n) {
	fac[0] = 1;
	for (int i = 1; i <= n; i++) {
		fac[i] = fac[i - 1] * i;
	}
	_fac[n] = ~fac[n];
	for (int i = n; i; i--) {
		_fac[i - 1] = _fac[i] * i;
	}

	s1[0][0] = 1;
	for (int i = 1; i <= n; i++) {
		s1[i][0] = 0, s1[i][i] = 1;
		for (int j = 1; j < i; j++) {
			s1[i][j] = s1[i - 1][j - 1] + s1[i - 1][j] * (i - 1);
		}
	}

	comb[0][0] = 1;
	for (int i = 1; i <= n; i++) {
		comb[i][0] = comb[i][i] = 1;
		for (int j = 1; j < i; j++) {
			comb[i][j] = comb[i - 1][j - 1] + comb[i - 1][j];
		}
	}
}

template <typename T>
T qpow(T a, ll p) {
	T rt = Zi(1), pa = a;
	for ( ; p; p >>= 1, pa = pa * pa) {
		if (p & 1) {
			rt = rt * pa;
		}
	}
	return rt;
}

namespace subtask1 {

typedef ComplexTemp<5> Complex;

const Zi inv2 ((Mod + 1) >> 1);
const Complex q1 (inv2, inv2), q2 (inv2, -inv2);
Complex pwq1[Kmx], pwq2[Kmx], pwqq[Kmx][Kmx];

Complex get_sum(int k1, int k2, ll n) {
	Complex x = pwq1[k1] * pwq2[k2];
	if (x == Zi(1))
		return Zi(n);
	return (pwqq[k1][k2] - 1) / (x - 1);
}

inline void init() {
	pwq1[0] = pwq2[0] = Zi(1);
	for (int i = 1; i < Kmx; i++) {
		pwq1[i] = pwq1[i - 1] * q1;
		pwq2[i] = pwq2[i - 1] * q2;
	}
}

Zi work(ll n, int K) {
	Complex coef = qpow(Complex(0, ~Zi(5)), K);
	Complex ret (0, 0);
	for (int k = 0; k <= K; k++) {
//		Complex tmp = get_sum(pwq1[k] * pwq2[K - k], n) * comb[K][k];
		Complex tmp = get_sum(k, K - k, n) * comb[K][k];
		if ((K - k) & 1) {
			ret = ret - tmp;
		} else {
			ret = ret + tmp;
		}
	}
	ret = ret * coef;
	assert(ret.v.v == 0);
//	cerr << n << " " << K << " " << ret.r.v << '\n';
	return ret.r;
}

Zi solve(ll n, int K) {
	Zi ans = 0;
	Complex q1n = qpow(q1, n + 1);
	Complex q2n = qpow(q2, n + 1);
	pwqq[0][0] = Zi(1);
	for (int i = 0; i <= K; i++) {
		for (int j = (i == 0); i + j <= K; j++) {
			pwqq[i][j] = ((!i) ? (pwqq[i][j - 1] * q2n) : (pwqq[i - 1][j] * q1n));
		}
	}
	for (int i = 1; i <= K; i++) {
		Zi tmp = work(n, i) * s1[K][i] * _fac[K];
		if ((K - i) & 1) {
			ans -= tmp;
		} else {
			ans += tmp;
		}
	}
	return ans;
}

void __main__(ll l, ll r, int K) {
	++l, ++r;
	Zi ans = solve(r, K) - solve(l - 1, K);
	ans = ans * ~Zi(r - l + 1);
	printf("%d\n", ans.v);
}

}

namespace subtask2 {

typedef ComplexTemp<3> Complex;

const Zi inv2 ((Mod + 1) >> 1);
const Zi inv3 ((Mod + 1) / 3);
const Zi inv6 = inv2 * inv3;
const Complex c1 (inv2, -inv6), c2 (inv2, inv6);
const Complex q1 (2, Mod - 1), q2 (2, 1);
Complex pwq1[Kmx], pwq2[Kmx], pwc1[Kmx], pwc2[Kmx];
Complex pwqq[Kmx][Kmx];

Complex get_sum(int k1, int k2, ll n) {
	Complex x = pwq1[k1] * pwq2[k2];
	if (x == Zi(1))
		return Zi(n);
	return (pwqq[k1][k2] - 1) / (x - 1);
}

inline void init() {
	pwq1[0] = pwq2[0] = pwc1[0] = pwc2[0] = Zi(1);
	for (int k = 1; k < Kmx; k++) {
		pwq1[k] = pwq1[k - 1] * q1;
		pwq2[k] = pwq2[k - 1] * q2;
		pwc1[k] = pwc1[k - 1] * c1;
		pwc2[k] = pwc2[k - 1] * c2;
	}
}

Zi work(ll n, int K) {
	Complex ret (0, 0);
	for (int k = 0; k <= K; k++) {
		Complex tmp = get_sum(k, K - k, n) * comb[K][k];
		Complex b = pwc1[k] * pwc2[K - k];
		tmp = tmp * b;
		ret = ret + tmp;
	}
	assert(ret.v.v == 0);
//	cerr << n << " " << K << " " << ret.r.v << '\n';
	return ret.r;
}

Zi solve(ll n, int K) {
	n >>= 1;
	Zi ans = 0;
	Complex q1n = qpow(q1, n + 1);
	Complex q2n = qpow(q2, n + 1);
	pwqq[0][0] = Zi(1);
	for (int i = 0; i <= K; i++) {
		for (int j = (i == 0); i + j <= K; j++) {
			pwqq[i][j] = ((!i) ? (pwqq[i][j - 1] * q2n) : (pwqq[i - 1][j] * q1n));
		}
	}
	for (int i = 1; i <= K; i++) {
		Zi tmp = work(n, i) * s1[K][i] * _fac[K];
		if ((K - i) & 1) {
			ans -= tmp;
		} else {
			ans += tmp;
		}
	}
	return ans;
}

void __main__(ll l, ll r, int K) {
	Zi ans = solve(r, K) - solve(l - 1, K);
	ans = ans * ~Zi(r - l + 1);
	printf("%d\n", ans.v);
}

}

int Case, ___;
ll l, r;
int K;
int main() {
	prepare(502);
	scanf("%d%d", &Case, &___);
	if (___ == 3) {
		subtask2::init();
	} else {
		subtask1::init();
	}
	while (Case--) {
		scanf("%lld%lld%d", &l, &r, &K);
		if (___ == 2) {
			subtask1::__main__(l, r, K);
		} else {
			subtask2::__main__(l, r, K);
		}
	}
	return 0;
}

　　然而注意到两个特征根的积不是 1 就是 -1，那么假设乘积是 1，考虑暴力展开 $(\lambda_1 \alpha^n + \lambda_2 \alpha^{-n})^{\overline{K}}$ 。

　　把 $\alpha^{n}$ 看做 $x$，大力分治 FFT。考虑最外层的求和符号后每一项变成 $\sum \alpha^{ni}$，简单算一下就行了。

　　如果乘积是 $-1$ 讨论一下奇偶性就行了。

　　时间复杂度 $O(K \log^2 K + K \log r)$

Code

#include <bits/stdc++.h>
using namespace std;
typedef bool boolean;

#define ll long long

void exgcd(int a, int b, int& x, int& y) {
  if (!b) {
    x = 1, y = 0;
  } else {
    exgcd(b, a % b, y, x);
    y -= (a / b) * x;
  }
}

int inv(int a, int n) {
  int x, y;
  exgcd(a, n, x, y);
  return (x < 0) ? (x + n) : (x);
}

const int N = 262144;
const int Mod = 998244353;
const int bzmax = 19;
const int g = 3;

template <const int Mod = :: Mod>
class Z {
  public:
    int v;

    Z() : v(0) {    }
    Z(int x) : v(x){    }
    Z(ll x) : v(x % Mod) {  }

    friend Z operator + (const Z& a, const Z& b) {
      int x;
      return Z(((x = a.v + b.v) >= Mod) ? (x - Mod) : (x));
    }
    friend Z operator - (const Z& a, const Z& b) {
      int x;
      return Z(((x = a.v - b.v) < 0) ? (x + Mod) : (x));
    }
    friend Z operator * (const Z& a, const Z& b) {
      return Z(a.v * 1ll * b.v);
    }
    friend Z operator ~(const Z& a) {
      return inv(a.v, Mod);
    }
    friend Z operator - (const Z& a) {
      return Z(0) - a;
    }
    Z& operator += (Z b) {
      return *this = *this + b;
    }
    Z& operator -= (Z b) {
      return *this = *this - b;
    }
    Z& operator *= (Z b) {
      return *this = *this * b;
    }
    friend boolean operator == (const Z& a, const Z& b) {
      return a.v == b.v;
    }
};

typedef Z<> Zi;

template <const int I>
class ComplexTemp {
  public:
    Zi r, v;

    ComplexTemp() : r(0), v(0) {    }
    ComplexTemp(int r) : r(r), v(0) { }
    ComplexTemp(Zi r) : r(r), v(0) {    }
    ComplexTemp(Zi r, Zi v) : r(r), v(v) {  }

    friend ComplexTemp operator + (ComplexTemp a, ComplexTemp b) {
      return ComplexTemp(a.r + b.r, a.v + b.v);
    }
    friend ComplexTemp operator - (ComplexTemp a, ComplexTemp b) {
      return ComplexTemp(a.r - b.r, a.v - b.v);
    }
    friend ComplexTemp operator * (ComplexTemp a, ComplexTemp b) {
      return ComplexTemp(a.r * b.r + a.v * b.v * I, a.r * b.v + a.v * b.r);
    }
    friend ComplexTemp operator / (ComplexTemp a, ComplexTemp b) {
      ComplexTemp c = b.conj();
      return a * c * ~((b * c).r);
    }
    friend ComplexTemp operator - (ComplexTemp a) {
      return ComplexTemp(-a.r, -a.v);
    }
    ComplexTemp conj() const {
      return ComplexTemp(r, -v);
    }
    friend ComplexTemp operator ~ (ComplexTemp a) {
      return ComplexTemp(1) / a;
    }
    boolean operator == (ComplexTemp b) {
      return r == b.r && v == b.v;
    }

    ComplexTemp& operator -= (ComplexTemp b) {
      return *this = *this - b;
    }
    ComplexTemp& operator += (ComplexTemp b) {
      return *this = *this + b;
    }
    ComplexTemp& operator *= (ComplexTemp b) {
      return *this = *this * b;
    }
};

template <typename T>
T qpow(T a, ll p) {
  if (p < 0) {
    a = ~a;
    p = -p;
  }
  T rt (1);
  for ( ; p; p >>= 1, a = a * a) {
    if (p & 1) {
      rt = rt * a;
    }
  }
  return rt;
}

class NTT {
  private:
    Zi gn[bzmax + 4], _gn[bzmax + 4];
  public:

    NTT() {
      for (int i = 0; i <= bzmax; i++) {
        gn[i] = qpow(Zi(g), (Mod - 1) >> i);
        _gn[i] = qpow(Zi(g), -((Mod - 1) >> i));
      }
    }

    template <typename T>
      void operator () (T* f, int len, int sgn) {
        for (int i = 1, j = len >> 1, k; i < len - 1; i++, j += k) {
          if (i < j)
            swap(f[i], f[j]);
          for (k = len >> 1; k <= j; j -= k, k >>= 1);
        }

        Zi *wn = (sgn > 0) ? (gn + 1) : (_gn + 1), w;
        T a, b;
        for (int l = 2, hl; l <= len; l <<= 1, wn++) {
          hl = l >> 1, w = 1;
          for (int i = 0; i < len; i += l, w = 1) {
            for (int j = 0; j < hl; j++, w *= *wn) {
              a = f[i + j], b = f[i + j + hl] * w;
              f[i + j] = a + b;
              f[i + j + hl] = a - b;
            }
          }
        }

        if (sgn < 0) {
          Zi invlen = ~Zi(len);
          for (int i = 0; i < len; i++) {
            f[i] *= invlen;
          }
        }
      }

    int correct_len(int len) {
      int m = 1;
      for ( ; m <= len; m <<= 1);
      return m;
    }
} NTT;

const Zi inv2 = (Mod + 1) >> 1;

namespace subtask1 {

  typedef ComplexTemp<5> Complex;

  typedef class Poly : public vector<Complex> {
    public:
      using vector<Complex>::vector;

      Poly& fix(int sz) {
        resize(sz);
        return *this;
      }
  } Poly;

  Poly operator * (Poly A, Poly B) {
    int n = A.size(), m = B.size();
    int k = NTT.correct_len(n + m - 1);
    if (n < 20 || m < 20) {
      Poly rt (n + m - 1, Complex(0, 0));
      for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
          rt[i + j] += A[i] * B[j];
        }
      }
      return rt;
    }
    A.resize(k), B.resize(k);
    NTT(A.data(), k, 1);
    NTT(B.data(), k, 1);
    for (int i = 0; i < k; i++) {
      A[i] *= B[i];
    }
    NTT(A.data(), k, -1);
    A.resize(n + m - 1);
    return A;
  }

  const Complex alpha (inv2, inv2), lambda (0, ~Zi(5));

  int K;
  Poly f1, f2;

  Poly dividing(int l, int r, int coef) {
    if (l == r) {
      return Poly {(coef == 1) ? lambda : -lambda, -Zi(l), lambda};
    }
    int mid = (l + r) >> 1;
    return dividing(l, mid, coef) * dividing(mid + 1, r, coef);
  }

  void prepare(int _K) {
    K = _K;
    f1 = dividing(0, K - 1, 0);
    f2 = dividing(0, K - 1, 1);
  }

  Zi calc(ll n) {
    auto calc = [&] (Complex a, ll n) {
      return (a == Complex(1)) ? (Complex(Zi((n + 1) % Mod))) : ((qpow(a, n + 1) - 1) / (a - 1));
    };
    Complex ans (0);
    for (int i = 0, _ = f1.size(); i < _; i++) {
      Complex z = qpow(alpha, (i - K));
      ans = ans + calc(z * z, n >> 1) * f1[i];
    }
    for (int i = 0, _ = f2.size(); i < _; i++) {
      Complex z = qpow(alpha, (i - K));
      ans = ans + calc(z * z, (n - 1) >> 1) * f2[i] * z;
    }
    assert(!ans.v.v);
    Zi fac = 1;
    for (int i = 1; i <= K; i++) {
      fac *= i;
    }
    ans.r *= ~fac;
    return ans.r;
  }

  Zi calc(ll l, ll r, int _K) {
    prepare(_K);
    return (calc(r + 1) - calc(l)) * ~Zi(r - l + 1);
  }

}

namespace subtask2 {
  typedef ComplexTemp<3> Complex;

  typedef class Poly : public vector<Complex> {
    public:
      using vector<Complex>::vector;

      Poly& fix(int sz) {
        resize(sz);
        return *this;
      }
  } Poly;

  Poly operator * (Poly A, Poly B) {
    int n = A.size(), m = B.size();
    int k = NTT.correct_len(n + m - 1);
    if (n < 20 || m < 20) {
      Poly rt (n + m - 1, Complex(0, 0));
      for (int i = 0; i < n; i++) {
        for (int j = 0; j < m; j++) {
          rt[i + j] += A[i] * B[j];
        }
      }
      return rt;
    }
    A.resize(k), B.resize(k);
    NTT(A.data(), k, 1);
    NTT(B.data(), k, 1);
    for (int i = 0; i < k; i++) {
      A[i] *= B[i];
    }
    NTT(A.data(), k, -1);
    A.resize(n + m - 1);
    return A;
  }

  const Zi inv2 ((Mod + 1) >> 1);
  const Zi inv3 ((Mod + 1) / 3);
  const Zi inv6 = inv2 * inv3;
  const Complex lambda1 (inv2, -inv6), lambda2 (inv2, inv6);
  const Complex alpha (2, Mod - 1);

  int K;
  Poly f;

  Poly dividing(int l, int r) {
    if (l == r) {
      return Poly {lambda2, -Zi(l), lambda1};
    }
    int mid = (l + r) >> 1;
    return dividing(l, mid) * dividing(mid + 1, r);
  }

  void prepare(int _K) {
    K = _K;
    f = dividing(0, K - 1);
  }

  Zi calc(ll n) {
    n >>= 1;
    auto calc = [&] (Complex a, ll n) {
      return (a == Complex(1)) ? (Complex(Zi((n + 1) % Mod))) : ((qpow(a, n + 1) - 1) / (a - 1));
    };
    Complex ans (0);
    for (int i = 0, _ = f.size(); i < _; i++) {
      Complex z = qpow(alpha, (i - K));
      ans = ans + calc(z, n) * f[i];
    }
    assert(!ans.v.v);
    Zi fac = 1;
    for (int i = 1; i <= K; i++) {
      fac *= i;
    }
    ans.r *= ~fac;
    return ans.r;
  }

  Zi calc(ll l, ll r, int _K) {
    prepare(_K);
    return (calc(r) - calc(l - 1)) * ~Zi(r - l + 1);
  }

}

int main() {
  ios::sync_with_stdio(false);
  int type, T;
  cin >> T >> type;
  ll l, r, K;
  while (T--) {
    cin >> l >> r >> K;
    Zi ans = type == 2 ? subtask1::calc(l, r, K) : subtask2::calc(l, r, K);
    printf("%d\n", ans.v);
  }
  return 0;
}