POJ-2002 Squares---绕点旋转+Hash

题目链接：

https://vjudge.net/problem/POJ-2002

题目大意：

有一堆平面散点集，任取四个点，求能组成正方形的不同组合方式有多少。

相同的四个点，不同顺序构成的正方形视为同一正方形。

解题思路：

直接四个点四个点地枚举肯定超时的，不可取。

普遍的做法是：先枚举两个点（这两个点是正方形的一条边），通过数学公式得到另外2个点，使得这四个点能够成正方形。然后检查散点集中是否存在计算出来的那两个点，若存在，说明有一个正方形。

但这种做法会使同一个正方形按照不同的顺序被枚举了四次，因此最后的结果要除以4.

已知点(x1, y1)，(x2, y2)，可求出下面两种可能

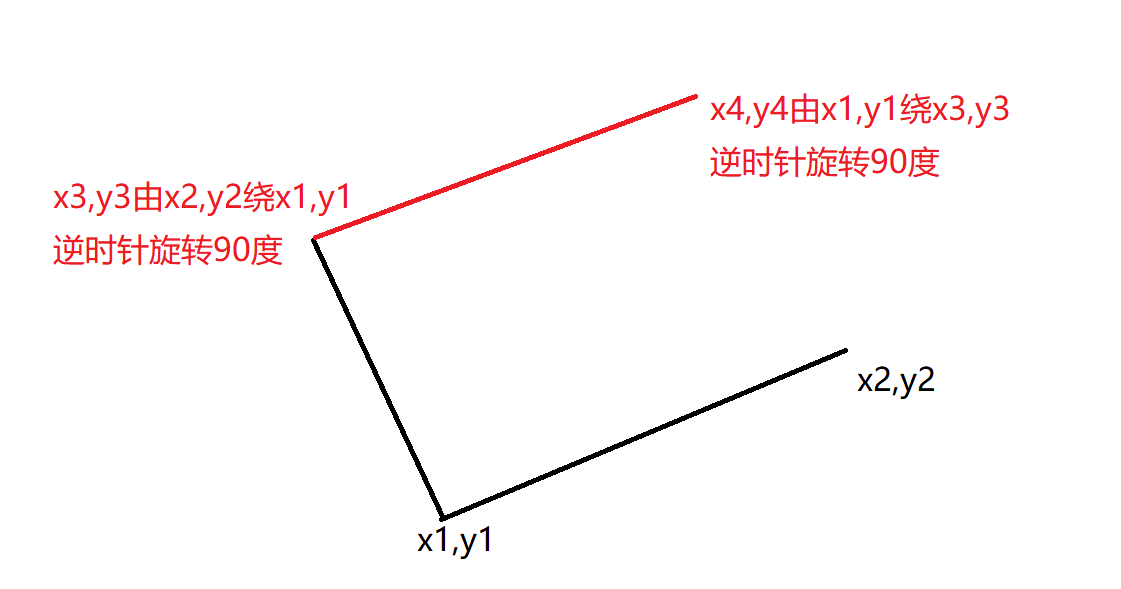
求出另外两个点之后直接在不在hash表中（之前用二分一直超时）

关于点(x1, y1)绕点(x0, y0)逆时针旋转β度得到(x2, y2)的公式：

 #include<iostream>
 #include<cstdio>
 #include<cstring>
 #include<string>
 #include<map>
 #include<set>
 #include<cmath>
 #include<algorithm>
 #include<vector>
 #define lowbot(i) (i&(-i))
 //#define Rotate(a, b) node(a.x + a.y - b.y, a.y + b.x - a.x)
 using namespace std;
 typedef long long ll;
 const int maxn =  + ;
 const int mod = ;
 struct node
 {
     int x, y;
     node(){}
     node(int x, int y):x(x), y(y){}
 };
 struct hashtable
 {
     int x, y;
     hashtable * next;
     hashtable()
     {
         next = ;
     }
 };
 hashtable * Hash[mod];
 void Hash_Insert(node a)
 {
     int key = (a.x * a.x + a.y * a.y) % mod;
     if(!Hash[key])
     {
         hashtable * p = new hashtable;
         p->x = a.x;
         p->y = a.y;
         Hash[key] = p;
     }
     else
     {
         hashtable *p = Hash[key];
         while(p->next)p=p->next;
         hashtable* temp = new hashtable;
         temp->x = a.x;
         temp->y = a.y;
         p->next = temp;
     }
 }
 bool Find(node a)
 {
     int key = (a.x * a.x + a.y * a.y) % mod;
     if(!Hash[key])return false;
     else
     {
         hashtable * temp = Hash[key];
         while(temp)
         {
             if(temp->x == a.x && temp->y == a.y)
                 return true;
             temp = temp->next;
         }
     }
     return false;
 }
 node a[maxn];

 node Rotate(node a, node b)//点b绕着点a逆时针旋转90度的坐标
 {
     int x = (b.x - a.x) *  - (b.y - a.y) *  + a.x;
     int y = (b.x - a.x) *  + (b.y - a.y) *  + a.y;
     return node(x, y);
 }

 int main()
 {
     int n;
     while(scanf("%d", &n) != EOF && n)
     {
         memset(Hash, , sizeof(Hash));
         for(int i = ; i <= n; i++)
         {
             scanf("%d%d", &a[i].x, &a[i].y);
             Hash_Insert(a[i]);
         }
         int ans = ;
         node x, y;
         for(int i = ; i <= n; i++)
         {
             for(int j = i + ; j <= n; j++)
             {
                 x = Rotate(a[i], a[j]);
                 y = Rotate(x, a[i]);
                 if(Find(x) && Find(y))ans++;
                 //cout<<i<<" "<<j<<" "<<x.x<<" "<<x.y<<" "<<y.x<<" "<<y.y<<endl;
                 x = Rotate(a[j], a[i]);
                 y = Rotate(x, a[j]);
                 if(Find(x) && Find(y))ans++;
             }
         }
         printf("%d\n", ans / );
     }
     return ;
 }