[51nod1264]线段相交

给定两个点:

typedef  struct {

double  x, y;

} Point;

Point A1,A2,B1,B2;

首先引入两个实验：

a.快速排斥实验

设以线段A1A2和线段B1B2为对角线的矩形为M,N;

若M,N 不相交，则两个线段显然不相交；

所以：满足第一个条件时：两个线段可能相交。

b.跨立实验

如果两线段相交，则两线段必然相互跨立对方.若A1A2跨立B1B2，则矢量( A1 - B1 ) 和(A2-B1)位于矢量(B2-B1)的两侧，

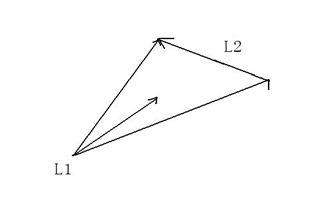
即(A1-B1) × (B2-B1) * (A2-B1) × (B2-B1)<0。

上式可改写成(A1-B1) × (B2-B1) * (B2-B1) × (A2-A1)>0。

应该判断两次，即两条线段都要为直线，判断另一直线的两端点是否在它两边，若是则两线段相交。

若积极满跨立实验是不行的，如下面的情况：

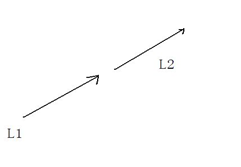
即两条线段在同一条直线上。所以我们要同时满足两次跨立和快速排斥实验。

总体分析：

当(A1-B1) × (B2-B1)=0时，说明(A1-B1)和(B2-B1)共线，但是因为已经通过快速排斥试验，所以 A1一定在线段 B1B2上；同理，(B2-B1)×(A2-B1)=0 说明A2一定在线段B1B2上。所以判断A1A2跨立B1B2的依据是：(A1-B1) × (B2-B1) * (B2-B1) × (A2-B1) >= 0。

同理判断B1B2跨立A1A2的依据是：(B1-A1) × (A2-A1) * (A2-A1) × (B2-A1) >= 0。

如图：

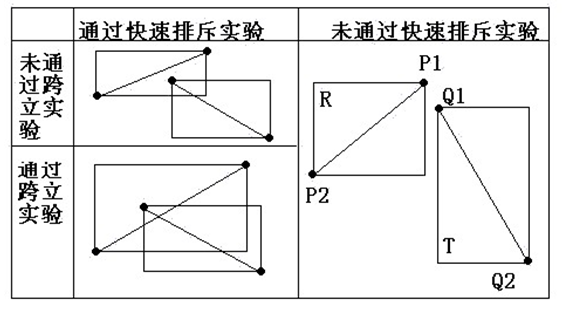
应用：

1.       判断两个线段相交

2.       判断线段与直线相交

3.       判断点在矩形内

模板题

 #include<bits/stdc++.h>
 using namespace std;
 typedef long long ll;
 struct line{
     double x1,y1,x2,y2;
 }p,q;
 double cross1(line &a,line &b){
     return (a.x1-b.x1)*(b.y2-b.y1)-(a.y1-b.y1)*(b.x2-b.x1);
 }
 double cross2(line &a,line &b){
     return (a.x2-b.x1)*(b.y2-b.y1)-(a.y2-b.y1)*(b.x2-b.x1);
 }
 bool judge(line &a,line &b){
     if(max(a.x1,a.x2)>=min(b.x1,b.x2)&&
         max(a.y1,a.y2)>=min(a.y1,a.y2)&&
         max(b.x1,b.x2)>=min(a.x1,a.x2)&&
         max(b.y1,b.y2)>=min(a.y1,a.y2)&&
         cross1(a,b)*cross2(a,b)<=&&
         cross1(b,a)*cross2(b,a)<=)
     return true;
     return false;
 }
 int main(){
     int t;
     cin>>t;
     while(t--){
         cin>>p.x1>>p.y1>>p.x2>>p.y2>>q.x1>>q.y1>>q.x2>>q.y2;
         if(judge(p,q)) cout<<"Yes\n";
         else cout<<"No\n";
     }
 }