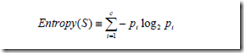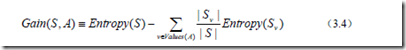决策树的基本ID3算法

一  ID3算法的大致思想

基本的ID3算法是通过自顶向下构造决策树来进行学习的。我们首先思考的是树的构造从哪里开始，这就涉及到选择属性进行树的构造了，那么怎样选择属性呢？为了解决这个问题，我们使用统计测试来确定每一个实例属性单独分类训练样例的能力，把分类能力最好的属性作为树根节点的测试。然后为根节点属性的每个可能值产生一个分支，并把训练样例排列到适当的分支之下。然后重复整个过程，用每个分支节点关联的训练样例来选取在该点被测试的最佳属性。这形成了对合格决策树的贪婪搜索，也就是算法从不回溯重新考虑以前的选择。

下面是ID3算法进行二分类的流程

从图中我们可以看出决策树的构造是一个递归的过程

二  熵（entropy）和信息增益（information gain）

ID3算法的核心问题是选取在树的每个结点要测试的属性，这里我们用属性的信息增益来衡量属性对训练样例的区分能力，属性的信息增益越大，表示区分能力越强。ID3算法在增长树的每一步使用信息增益标准从候选属性中选择属性。

首先在这里说一下 熵的概念，在信息论中广泛使用的一个度量标准，称为熵，它刻画了任意样例集的纯度。

给定包含关于某个目标概念的正反样例的样例集S，那么S相对这个布尔型分类的熵为：
Entropy(S) ≡-p⊕log2p⊕-pΘlog2pΘ

其中p⊕是S中正例的比例，pΘ是在S中反例的比例。如果S的所有成员属于同一类，辣么S的熵为0，当集合中正反样例的数量相等时熵为1，其他情况介于0和1之间。

上面是关于目标分类为bool类型下的熵，更一般的，如果目标属性具有c个不同的值，那么S相对于c个状态的分类的熵定义为：

其中pi 是S中属于类别i的比例。

用信息增益度量期望的熵降低

有了熵作为衡量训练样例集合纯度的标准，现在可以定义属性分类数据的效力的度量标准。这个标准被称为信息增益。简单的说，一个属性的信息增益就是由于使用这个属性分割样例而导致的期望熵降低。更精确地说，一个属性A相对样例集合S的信息增益Gain(S,A)被定义为：

其中Values(A)是属性A所有可能值的集合，Sv是属性A的值为v的子集。等式的第一项就是原来集合S的熵，第二项是用A分类S后熵的期望值。这个第二项描述的期望熵就是每个子集的熵的加权和，权值为属于Sv的样例占原始样例S的比例，所以Gain（S，A）是由于知道属性A的值而导致的期望熵减少。

三 使用python实现一个简单的决策树的生成

1. 计算数据集的香农熵

 """
 Created on Sat May 14 13:58:26 2016

 @author: MyHome
 """
 '''计算给定数据集的香农熵'''

 from math import log

 def calcShannonEnt(dataSet):
     numEntries = len(dataSet)
     labelCounts = {}
     for featVec in dataSet:
         currentLabel = featVec[-1]
         labelCounts[currentLabel] = labelCounts.get(currentLabel,0) + 1
     shannonEnt = 0.0
     for key in labelCounts:
         pro = float(labelCounts[key])/numEntries
         shannonEnt = -pro * log(pro,2)

     return shannonEnt

2.创建数据

 def createDataSet():

     dataSet = [['Sunny','Hot','High','Weak','No'],['Sunny','Hot','High','Strong','No'],\
               ['Overcast','Hot','High','Weak','Yes'],['Rain','Mild','High','Weak','Yes'],\
               ['Rain','Cool','Normal','Weak','Yes'],['Rain','Cool','Normal','Strong','No'],\
               ['Overcast','Cool','Normal','Strong','Yes'],['Sunny','Mild','High','Weak','No'],\
               ['Sunny','Cool','Normal','Weak','Yes'],['Rain','Mild','Normal','Weak','Yes'],\
               ['Sunny','Mild','Normal','Strong','Yes'],['Overcast','Mild','High','Strong','Yes'],\
               ['Overcast','Hot','Normal','Weak','Yes'],['Rain','Mild','High','Strong','No']]

     labels = ['Outlook','Temperature','Humidity','Wind']
     return dataSet,labels

3.按照给定的特征划分数据集（根据某一属性的属性值对数据集进行划分）

 def splitDataSet(dataSet,axis,value):
     retDataSet = []
     for featVec in dataSet:
         if featVec[axis] == value:
             reducedFeatVec = featVec[:axis]
             reducedFeatVec.extend(featVec[axis + 1 :])
             retDataSet.append(reducedFeatVec)

     return retDataSet
 

4.计算数据集中各属性的信息增益，选出当前最佳分类属性

 def chooseBestFeatureToSplit(dataSet):
     numFeatures = len(dataSet[0]) - 1
     baseEntropy = calcShannonEnt(dataSet)
     bestInfoGain = 0.0
     bestFeature = -1
     for i in range(numFeatures):
         featList = [example[i] for example in dataSet]
         uniqueVals = set(featList)
         newEntropy = 0.0
         for value in uniqueVals:
             subDataSet =  splitDataSet(dataSet,i,value)
             prob = len(subDataSet)/float(len(dataSet))
             newEntropy += prob *calcShannonEnt(subDataSet)
         infoGain = baseEntropy - newEntropy
         if (infoGain >bestInfoGain):
             bestInfoGain = infoGain
             bestFeature = i
     return bestFeature
 

5.如果数据集已经处理了所有属性，但是类标签依然不是唯一的，此时我们需要决定如何定义该叶子节点，在这种情况下，我们通常会采用多数表决的方法决定该叶子节点的分类

 def majorityCnt(classList):
     classCount = {}
     for vote in classList:
         if vote not in classCount.keys():
             classCount[vote] = 0
         classCount[vote] += 1

         sortedClassCount = sorted(classCount.iteritems(),key = operator.itemgetter(1),reverse = True)

         return sortedClassCount[0][0]
 

6. 构造树

 def createTree(dataSet,labels):
     classList = [example[-1] for example in dataSet]
     if classList.count(classList[0]) == len(classList):
         return classList[0]
     if len(dataSet[0]) == 1:
         return majorityCnt(classList)
     bestFeat = chooseBestFeatureToSplit(dataSet)
     bestFeatLabel = labels[bestFeat]
     myTree = {bestFeatLabel:{}}
     del(labels[bestFeat])
     featValues = [example[bestFeat] for example in dataSet]
     uniqueVals = set(featValues)
     for value in uniqueVals:
         subLabels = labels[:]
         myTree[bestFeatLabel][value] = createTree(splitDataSet(dataSet,bestFeat,value),subLabels)
     return myTree

7.运行结果

 dataSet,labels = createDataSet()

 createTree(dataSet,labels)
 Out[10]:
 {'Outlook': {'Overcast': 'Yes',
   'Rain': {'Wind': {'Strong': 'No', 'Weak': 'Yes'}},
   'Sunny': {'Humidity': {'High': 'No', 'Normal': 'Yes'}}}}
 

根据结果我们可以画出决策树

四 总结

我们通过不断选取当前最佳属性来把数据集进行划分，直到遍历所有属性或每个分支下的所有样例都为同一类为止，这是一个不断递归生成树的过程。