[HNOI2009]双递增序列(洛谷P4728)+小烈送菜(内部训练题)——奇妙的dp
博主学习本题的经过嘤嘤嘤:
7.22 : 听学长讲(一知半解)——自己推(推不出来)——网上看题解——以为自己会了(网上题解是错的)——发现错误以后又自己推(没推出来)——给学长发邮件——得到正确解法——按着学长思路又推一遍——最后理解
(前后的“学长”不是同一个人)
7.23 : 写出代码,完善细节。
(建议改成:西 天 取 经)
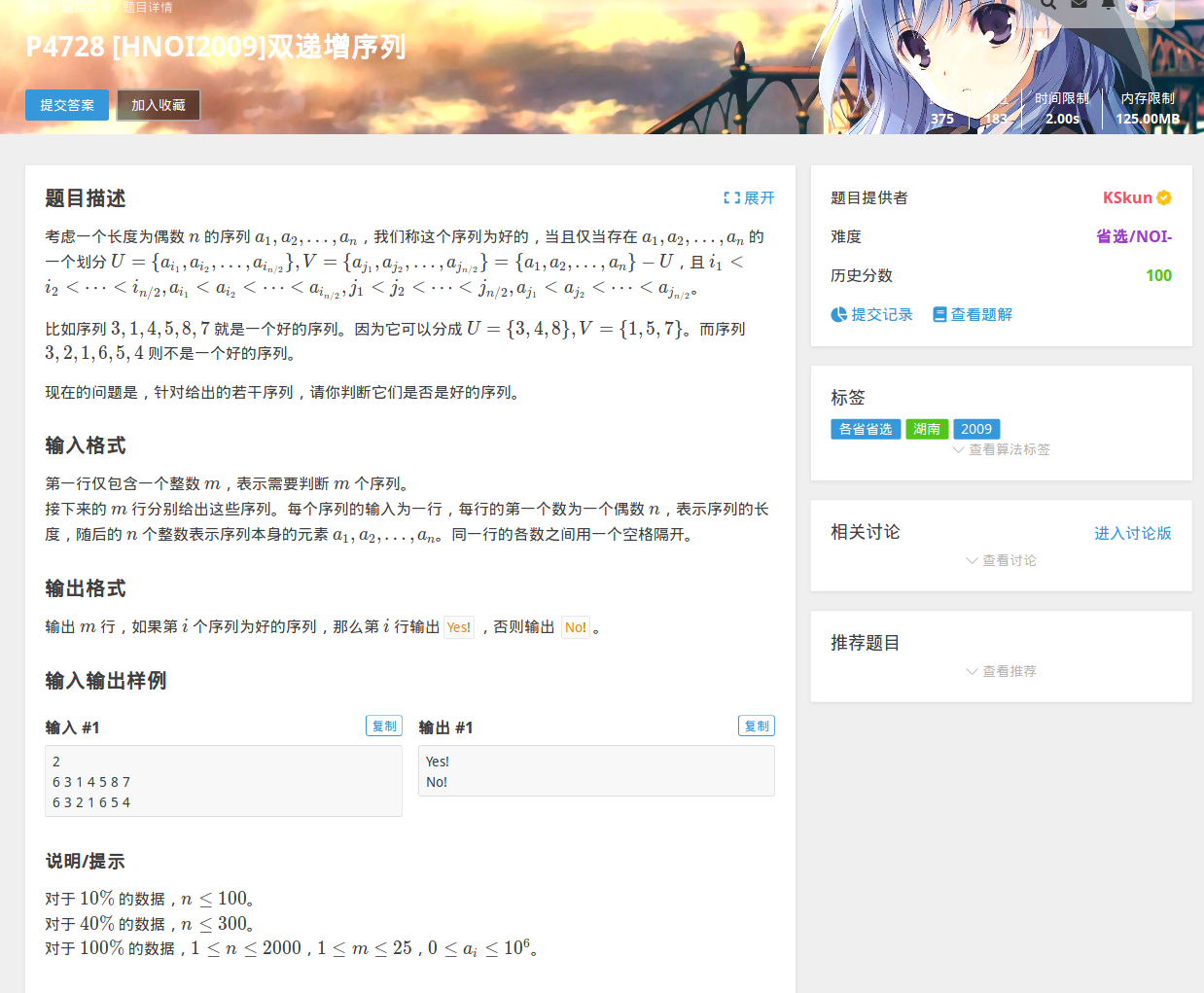
首先,网上对于这道题的题解绝大部分是错误的!(比如洛谷上的部分题解)
用LIS做是不行的
玄学贪心是不行的
dp转移方程不能自圆其说是不行的
即使是AC代码也不一定是正确的(2009年的省选,数据太太太太太太太太太太太太太太水了嘤嘤嘤)
废话说完了
~~~~~~~~~~~~~~~嘤嘤嘤来自蒟蒻OIerOrzer的分割线啦嘤嘤嘤~~~~~~~~~~~~~~~~
以下为正文部分嘤嘤嘤:
考虑把一个数列分成两个集合,有a[i]的为一个集合,没有a[i]的为一个集合~
我们定义状态转移方程dp[i][j]表示对于前i个数,有a[i]的集合的长度为j,没有a[i]的集合的最后一个数的最小值为dp[i][j](神仙定义)
也就是说,现在有两个集合,其中一个有a[i],另一个没有a[i]。尝试把a[i+1]放到其中一个集合中。
1.尝试把a[i+1]放到有a[i]的集合当中。那么需要满足的先决条件就是:a[i+1]>a[i].
此时更新dp[i+1][j+1](因为把a[i]放到长度为j的集合中,于是长度++)此时没有a[i+1]的集合同时也是没有a[i]的集合,换句话来说,这个转移对没有a[i]的集合是没有改变的,所以,dp[i+1][j+1]可以直接由dp[i][j]继承过来。
2.尝试把a[i+1]放到没有a[i]的集合当中。那么需要满足的先决条件就是:a[i+1]>dp[i][j].
此时更新dp[i+1][i-j+1](原来没有a[i]的集合的长度为(i-j),把a[i+1]放进去,长度++)既然把a[i+1]放到了没有a[i]的集合中,那么,没有a[i+1]的集合的最后一个数就是a[i],于是,用a[i]去更新dp[i+1][i-j+1];
(真绕啊嘤嘤嘤)
上代码嘤嘤嘤:
1 #include <bits/stdc++.h>
2 using namespace std;
3 const int maxn=2000+10;
4 int dp[maxn][maxn],a[maxn];
5 int n,m;
6 void Solve(){
7 scanf("%d",&m);
8 while(m--){
9 scanf("%d",&n);
10 memset(dp,0x3f,sizeof(dp));
11 memset(a,0x3f,sizeof(a));
12 for(int i=1;i<=n;++i) scanf("%d",&a[i]);
13 dp[1][1]=-1;//因为数据中可能有0,因此不能初始化为0;
14 for(int i=1;i<=n;++i){
15 for(int j=1;j<=i;++j){
16 if(a[i+1]>a[i]) dp[i+1][j+1]=min(dp[i+1][j+1],dp[i][j]);
17 if(a[i+1]>dp[i][j]) dp[i+1][i-j+1]=min(dp[i+1][i-j+1],a[i]);
18 }
19 }
20 if(dp[n][n/2]>1e8) printf("No!\n");
21 //没有更新,说明不能将原序列合法地平分成两部分,就输出No;
22 else printf("Yes!\n");
23 }
24 }
25 int main(){
26 Solve();
27 return 0;
28 }
完结撒花嘤嘤嘤~(然而并没有)

上辈子的题了(大雾)(所以这就是火星水吗)
但是在解决上一道题后会发现对于这道题会有不一样的理解~~~
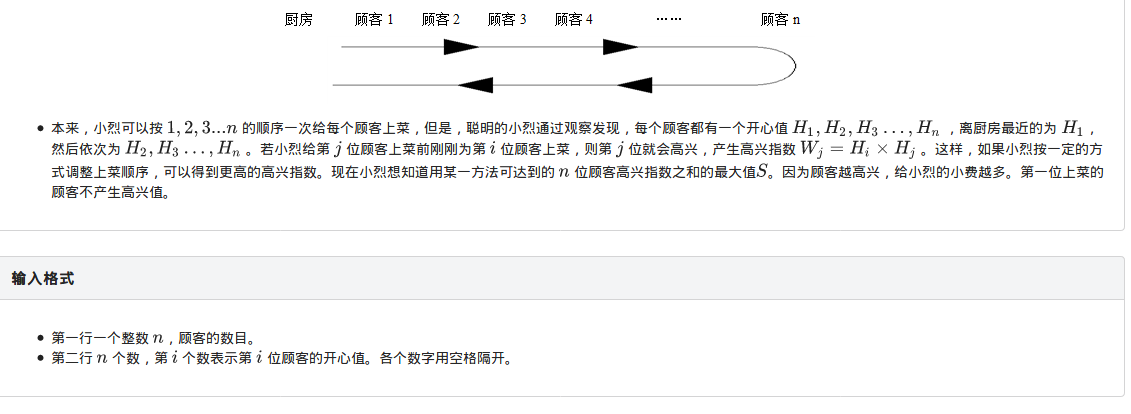
我们先定义dp[i][j]表示小烈1走到i,小烈2走到j时的最大收益。且默认小烈1始终在小烈2前面,且前j个已经被送完。
换句话来说,其实根本没有小烈1和小烈2(只是我们yy出来的)或者说,并不是划分了“小烈1”和“小烈2”这两个抽象的概念,划分的应该是“送了a[i]的小烈”和“没有送a[i]的小烈”!
(woc这不就是上一道题吗,太像了好叭)
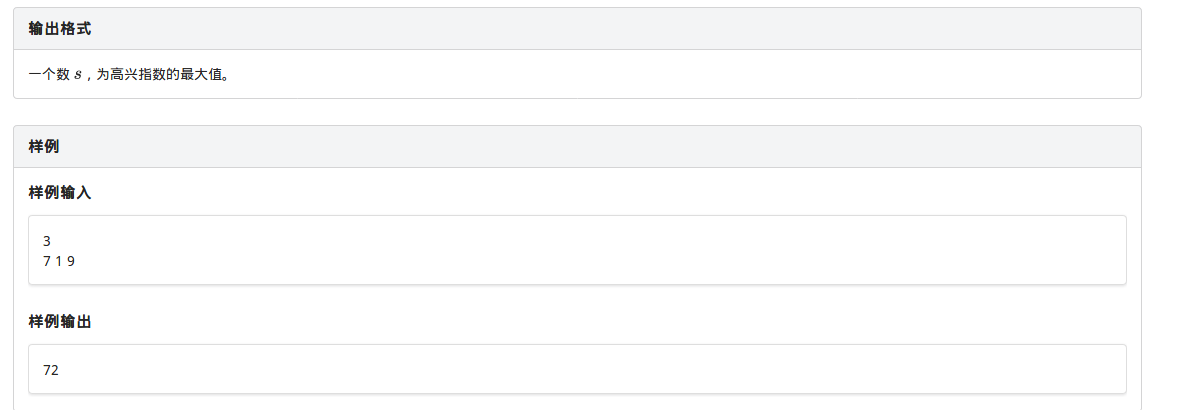
现在我们换一种表达方式来定义dp[i][j]:
dp[i][j]表示前i个客人,没有送过a[i]的小烈最后一个送的是a[j]时的最大收益。
默认j小于i,且前j个一定已经送过了(如果前j个有没有送过的,那就不合法了,因为两个小烈不能回头)
现在考虑a[i+1]由谁送。
1.由送了a[i]的小烈送。所以,没有送a[i]的小烈同样没有送a[i+1]。也就是说,这个转移完成后,没有送a[i]的小烈原来在j,现在还是在j,没有变化。
所以用(dp[i][j]+a[i]*a[i+1])更新(dp[i+1][j])。
2.由没有送a[i]的小烈送。所以,送了a[i]的小烈没有送a[i+1]。也就是说,没有送a[i+1]的小烈最后一个送的是a[i]!
所以用(dp[i][j]+a[j]*a[i+1])更新(dp[i+1][i]).
(和刚才那个一样绕嘤嘤嘤)
上代码:


1 #include <bits/stdc++.h>
2 using namespace std;
3 const int maxn=2500+10;
4 int dp[maxn][maxn],a[maxn],ans;
5 void Solve(){
6 int n;scanf("%d",&n);
7 for(int i=1;i<=n;++i) scanf("%d",&a[i]);
8 for(int i=1;i<=n;++i){
9 for(int j=0;j<i;++j){//j的范围要搞清楚哦;
10 dp[i+1][j]=max(dp[i+1][j],dp[i][j]+a[i]*a[i+1]);
11 dp[i+1][i]=max(dp[i+1][i],dp[i][j]+a[j]*a[i+1]);
12 }
13 }
14 for(int i=0;i<n;++i) ans=max(ans,dp[n][i]+a[i]*a[n]);
15 /*现实中的小烈是从1走到n,又从n回去,在dp方程里面我们把一个小烈拆成了两个,
16 其中一个表示现实中正向走的部分,另一个表示现实中反向走的部分(但是令这一个
17 反向走的小烈反过来走,就是正着走)也就是说,当现实中小烈走到n,开始返回的
18 时候,a[n]与dp方程中定义的小烈2经过的最后一个a[i](也就是反着走的第一个
19 a[i])是要产生一个值的,而这个值要加到答案里面才能得到最终结果*/
20 printf("%d",ans);
21 }
22 int main(){
23 Solve();
24 return 0;
25 }
嘤嘤嘤
完结撒花花!!!
[HNOI2009]双递增序列(洛谷P4728)+小烈送菜(内部训练题)——奇妙的dp的更多相关文章
- 【BZOJ1489】[HNOI2009]双递增序列(动态规划)
[BZOJ1489][HNOI2009]双递增序列(动态规划) 题面 BZOJ 洛谷 题解 这\(dp\)奇奇怪怪的,设\(f[i][j]\)表示前\(i\)个数中,第一个数列选了\(j\)个数,第二 ...
- 小烈送菜——奇怪的dp
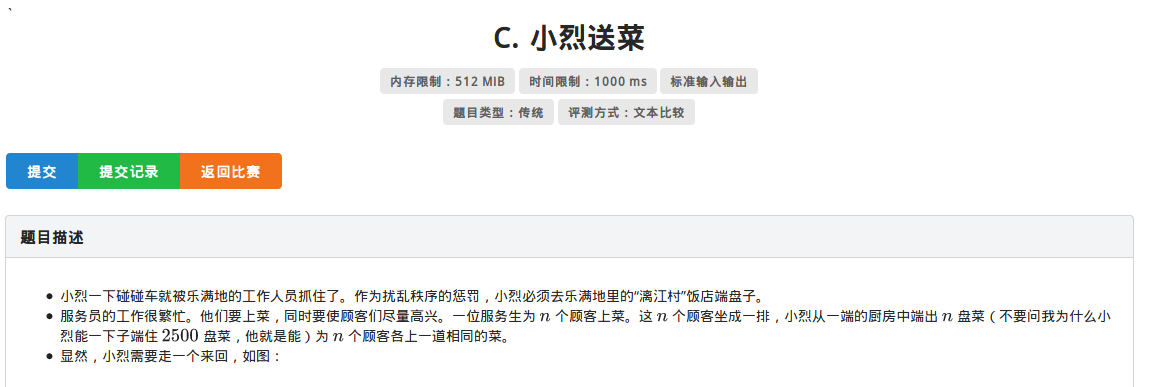
小烈送菜 题目描述 小烈一下碰碰车就被乐满地的工作人员抓住了.作为扰乱秩序的惩罚,小烈必须去乐满地里的"漓江村"饭店端盘子. 服务员的工作很繁忙.他们要上菜,同时要使顾客们尽量高兴 ...
- 线性DP之小烈送菜
小烈送菜 小烈一下碰碰车就被乐满地的工作人员抓住了.作为扰乱秩序的惩罚,小烈必须去乐满地里的"漓江村"饭店端盘子. 服务员的工作很繁忙.他们要上菜,同时要使顾客们尽量高兴.一位服务 ...
- 方格取数(简单版)+小烈送菜(不知道哪来的题)-----------奇怪的dp增加了!
一.方格取数: 设有N*N的方格图(N<=20),我们将其中的某些方格中填入正整数,而其他的方格中则放入数字0. 某人从图的左上角的A(1,1) 点出发,可以向下行走,也可以向右走,直到到达右下 ...
- 【题解】洛谷P1373 小a和uim之大逃离(坐标DP)
次元传送门:洛谷P1373 思路 设f[i][j][t][1/0]表示走到(i,j)时 小a减去uim的差值为t 当前是小a取(0) uim取(1) 那么转移就很明显了 f[i][j][t][]=(f ...
- P4728 [HNOI2009]双递增序列
题意 这个DP状态有点神. 首先考虑一个最暴力的状态:\(f_{i,j,k,u}\)表示第一个选了\(i\)个,第二个选了\(j\)个,第一个结尾为\(k\),第二个结尾为\(u\)是否可行. 现在考 ...
- [luogu4728 HNOI2009] 双递增序列 (dp)
传送门 Solution 前几天刚做了类似题,这种将一个序列拆分为两个单调序列的题一般都是设\(dp[i]\)表示i为一个单调序列的末尾时,另一个序列的末尾是多少 然后应用贪心的思想,在这道题中就是让 ...
- [HNOI2009]双递增序列(动态规划,序列dp)
感觉这个题还蛮难想的. 首先状态特别难想.设\(dp[i][j]\)表示前i个数,2序列的长度为j的情况下,2序列的最后一个数的最小值. 其中1序列为上一个数所在的序列,2序列为另外一个序列. 这样设 ...
- [HNOI2009]双递增序列
不难发现本题贪心是不好做的,可以考虑 \(dp\). 首先的一个想法就是令 \(dp_{i, j, k, l}\) 表示当前选到第 \(i\) 个位置,当前第一个序列选了 \(j\) 个数,当前第一个 ...
随机推荐
- PULPino datasheet中文翻译并给了部分论文注释(前四章:Overview、Memory Map、CPU Core、Advanced Debug Unit)
参考: (1).PULPino datasheet:https://github.com/pulp-platform/pulpino/blob/master/doc/datasheet/datashe ...
- freeswitch刷新网关方法
1.freeswitch xml配置文件新增网关后,使其生效,可以重启freeswitch或者使用命令方式 fs_cli -H 127.0.0.1 -P 8021 -p hmzj -x sofia p ...
- node实战小例子
第一章 2020-2-6 留言小本子 思路(由于本章没有数据库,客户提交的数据放在全局变量,接收请求用的是bodyParser, padyParser使用方法 app.use(bodyParser.u ...
- 简单入门PHP中的多字节字符串操作
什么是多字节的字符串操作呢?其实不少的同学可能都已经使用过了,但我们还是要从最基础的问题说起. 一个字符占几个字节并不是我们表面上看到的那样.正常情况下,一个数字或英文以及英文符号都是占用一个字节的. ...
- PHP的OpenSSL加密扩展学习(一):对称加密
我们已经学过不少 PHP 中加密扩展相关的内容了.而今天开始,我们要学习的则是重点中的重点,那就是 OpenSSL 加密扩展的使用.为什么说它是重点中的重点呢?一是 OpenSSL 是目前 PHP 甚 ...
- wordpress 搭建
wordpress 搭建: 公司要使用自建地图.选用了国外的Mapplic .但是Mapplic不支持直接编辑地图,需要用json的格式定义.但是wordpress版本的就有这个鬼东西,所以搞了一个这 ...
- 完美解决JavaIO流报错 java.io.FileNotFoundException: F:\ (系统找不到指定的路径。)
完美解决JavaIO流报错 java.io.FileNotFoundException: F:\ (系统找不到指定的路径.) 错误原因 读出文件的路径需要有被拷贝的文件名,否则无法解析地址 源代码(用 ...
- CF755G-PolandBall and Many Other Balls【倍增FFT】
正题 题目链接:https://www.luogu.com.cn/problem/CF755G 题目大意 \(n\)个东西排成一排,每个组可以选择一个单独的物品或者两个连续的物品,一个物品不同同时在两 ...
- Hyper-V CPU设置
前言 最近在用Hyper-V测试项目,发现在运行过程中发现项目总数崩掉,几经发现有一个共性,CPU占用率100%,分析问题发现问题出在Hyper-V CPU设置上,Hyper-V装系统就不赘述了,网上 ...
- Hutool时间和日期相关工具
日期时间工具 获取当前时间(1) public class HDateAndTime { public static void main(String[] args) { //获取当前时间 Date ...
